Contents
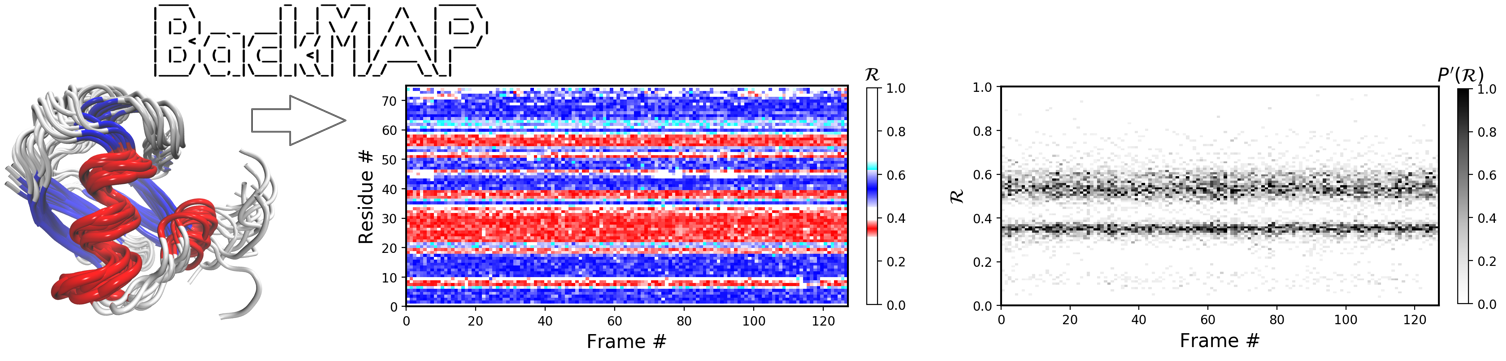
BackMAP is a Python module (and stand-alone tool) that helps with the visualization of large amounts of structural (space-time) backbone data in a single graph. It utilizes a new per-residue backbone metric -- the Ramachandran number -- to provide easily readable "pictures" (multi-angle pictures or MAPS) of protein conformations, ensembles, and trajectories. Input structures can be either a combined protein databank (PDB) structure file, or a directory of such files, and produces graphs.
Running the following at a command prompt (terminal) would get the job done (the '-I' is not necessary, but ensures the latest sub-version is installed):
$ pip install -I backmap$ git clone https://github.com/ranjanmannige/backmap.git
$ cd backmap
$ python setup.py install
$ python setup.py testFrom the git repository download the zip (https://github.com/ranjanmannige/backmap/archive/master.zip). At a command prompt, unzip and change directory into the extracted directory (cd ./backmap/) and perform the following commands.
$ python setup.py install
$ python setup.py testimport backmap as bm
print bm.R(phi=0,psi=0) # Should print '0.5'For more information about in-script module usage, refer to the manuscript associated with this module.
After installation, the following commands produce a variety of graphs (exampled below).
$ python -m backmap -pdb ./pdbs/ProteinDatabankStructureFilename.pdb
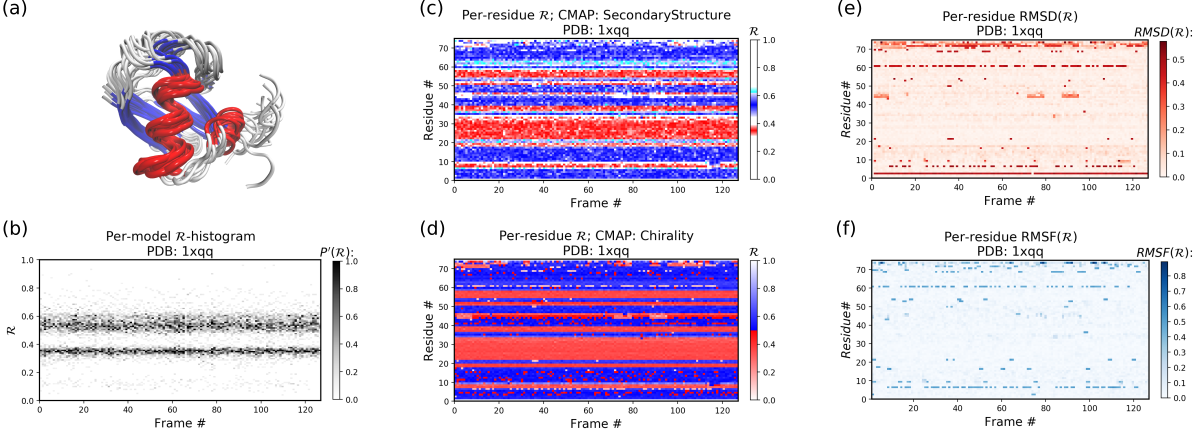
$ python -m backmap -pdb /directory/containing/pdbs/4.1 Example 1: A stable protein (1xqq)
The Panels (b) through (f) were created by running the following command within thin the downloaded directory (Panel (a) was created using VMD).
$ python -m backmap -pdb ./tests/pdbs/1xqq.pdbAs evident below, the graphs generated from the protein ensemble 1xqq describes a conformationally stable protein (each graph is detailed below).
Each column in Panel (b) describes the histogram in Ramachandran number (R) space for a single model/timeframe. These histograms show the presence of both helices (at R ~ 0.34) and sheets (at R ~ 0.52). Additionally, Panels (c) and (d) describe the per-residue conformational plots (colored by two different metrics or CMAPs), which show that most of the protein backbone remains relatively stable (e.g., few fluctuations in state or 'color' are evident over the frame #). Finally, Panel (e) describes the extent towards which a single residue's state has deviated from the first frame, and Panel (f) describes the extent towards which a single residue's state has deviated from its state in the previous frame. Both these graphs, as expected from Panels (c) and (d), show that this protein is relatively conformationally stable.
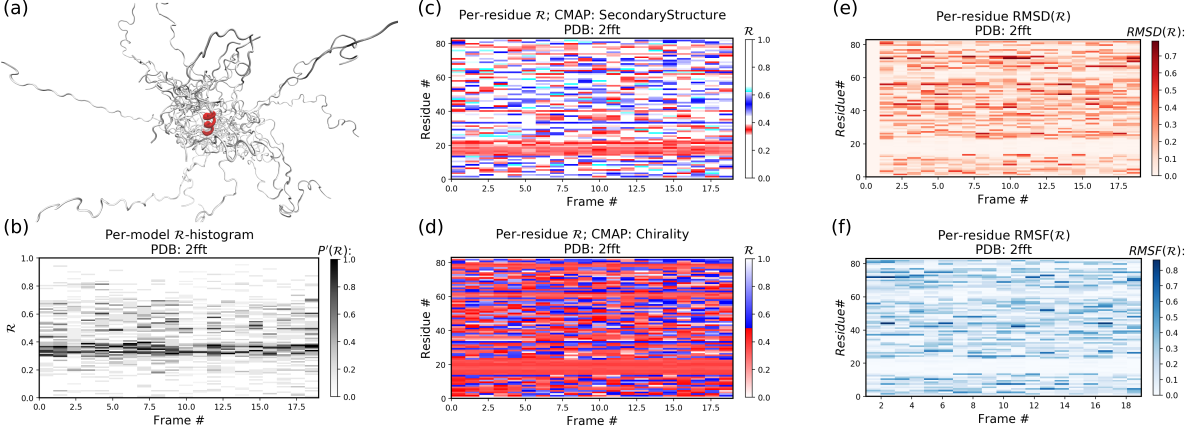
4.2 Example 2: An intrinsically disordered protein (2fft)
As compared to the conformationally stable protein above, an intrinsically disordered protein 2fft is much more flexible
Panel (b) shows that the states accessed per model are diverse and dramatically fluctuate over the entire range of R (this is especially true when compared to a stable protein, see above).
The diverse states occupied by each residue (Panels (c) and (d)) confirm this conformational variation within most residues (Panels (e) and (f) similarly show how most of the residues fluctuate dramatically).
Yet, interestingly, Panels (c) through (f) also show an unusually stable region -- residues 15 through 25 -- which consistently display the same conformational (alpha-helical) state at R ~ 0.33 (interpreted as the color red in Panel (c)). This trend would be hard to recognize by simply looking at the structure (Panel (a)).
The Ramachandran number concept is discussed in the following manuscripts (this tool is discussed in the first reference):
- Mannige (2018) "The Backmap Python Module: How a Simpler Ramachandran Number Can Simplify the Life of a Protein Simulator" PeerJ. Accepted [Manuscript PDF].
- Mannige, Kundu, Whitelam (2016) "The Ramachandran Number: An Order Parameter for Protein Geometry" PLoS ONE 11(8): e0160023 [Journal Link].