The MATLAB scripts in this repo theoretically demonstrate the versatility of phased-array antennas compared to other antenna topologies (i.e. dipoles, horns, etc.). The radiation pattern of phased-array antennas can be electronically steered and shaped, while for other antenna topologies the radiation pattern is practically fixed.
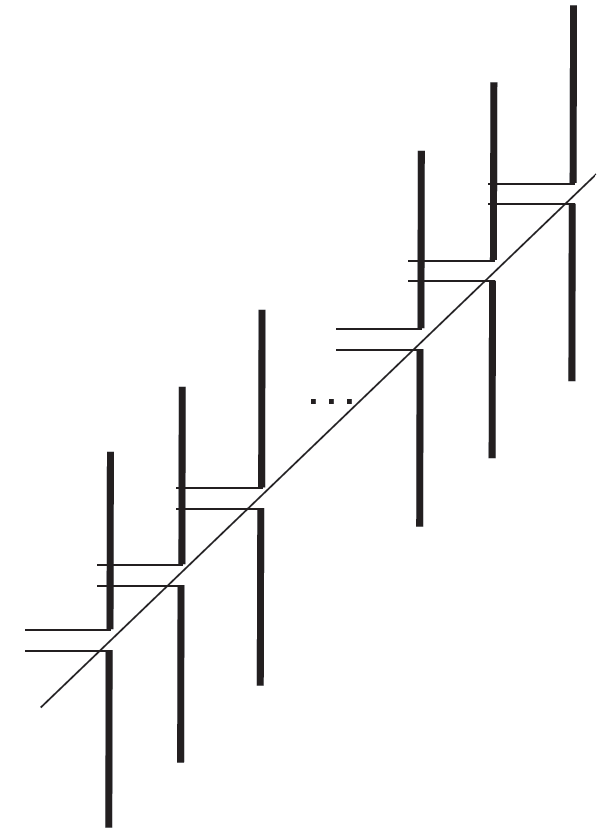
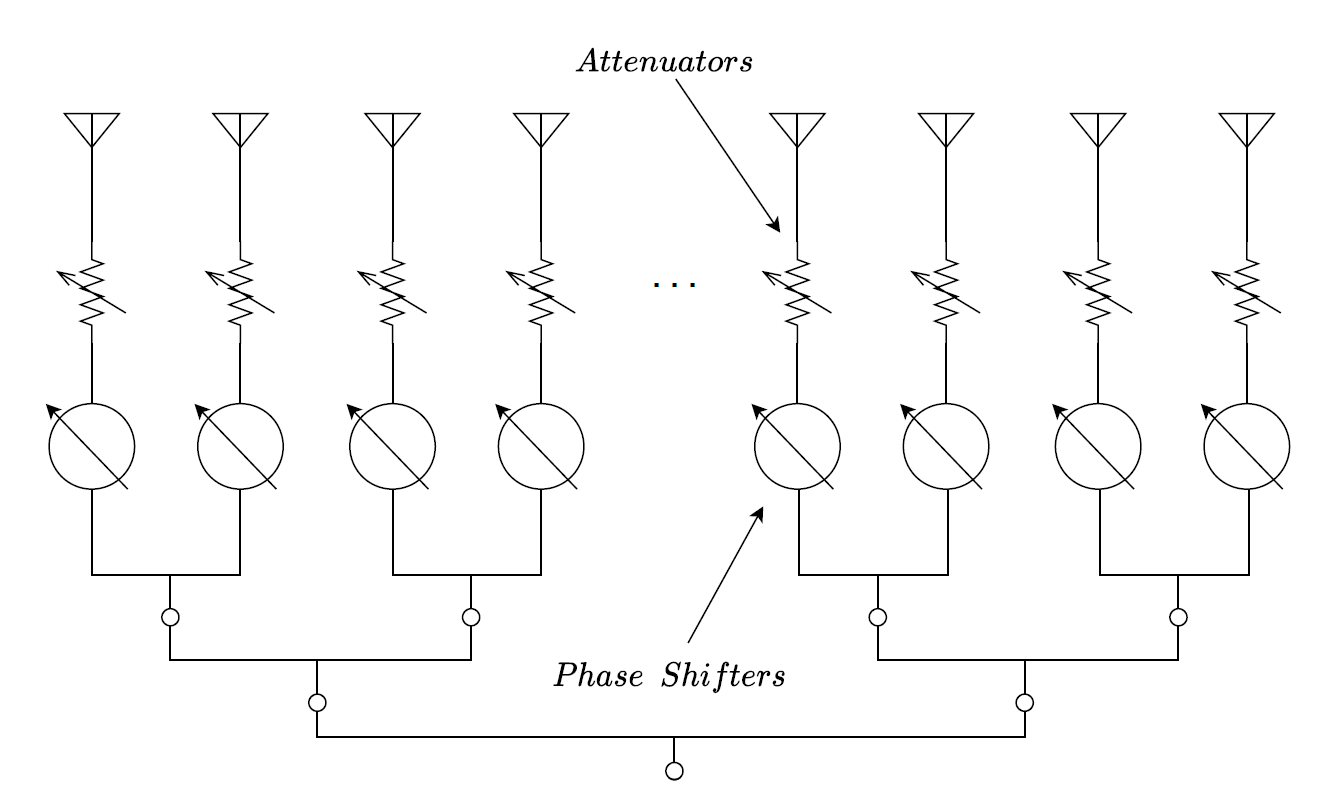
Phased-array antennas are constructed by arranging a number of individual antennas (dipoles, horns, etc.) to form an array. In the array, attenuators and phase shifters can be used to control the magnitude and phase of the signal feeding each antenna.
Dipoles forming a linear Phased-Array Antenna (1st) and complete circuit diagram (2nd)
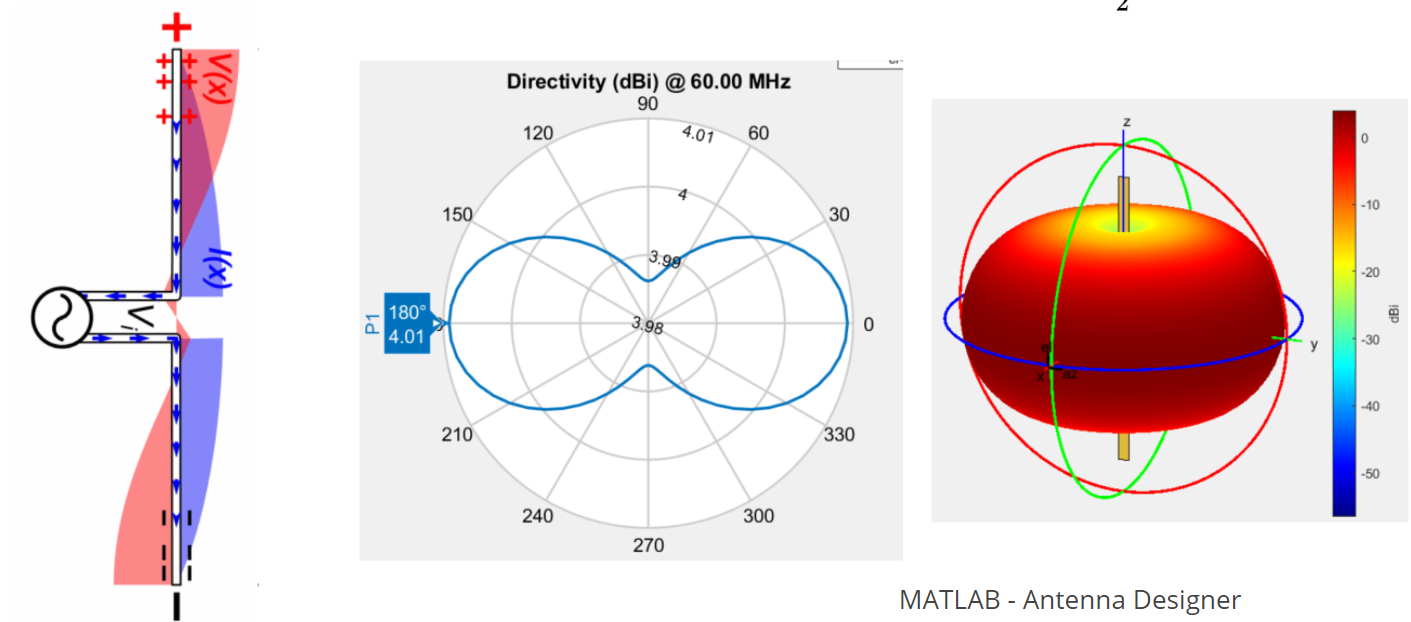
Given the voltage and current distributions present in an antenna when energized, the corresponding E-field and H-field can be calculated. Consequently the radiation pattern can be found from the time-average Poynting Vector:
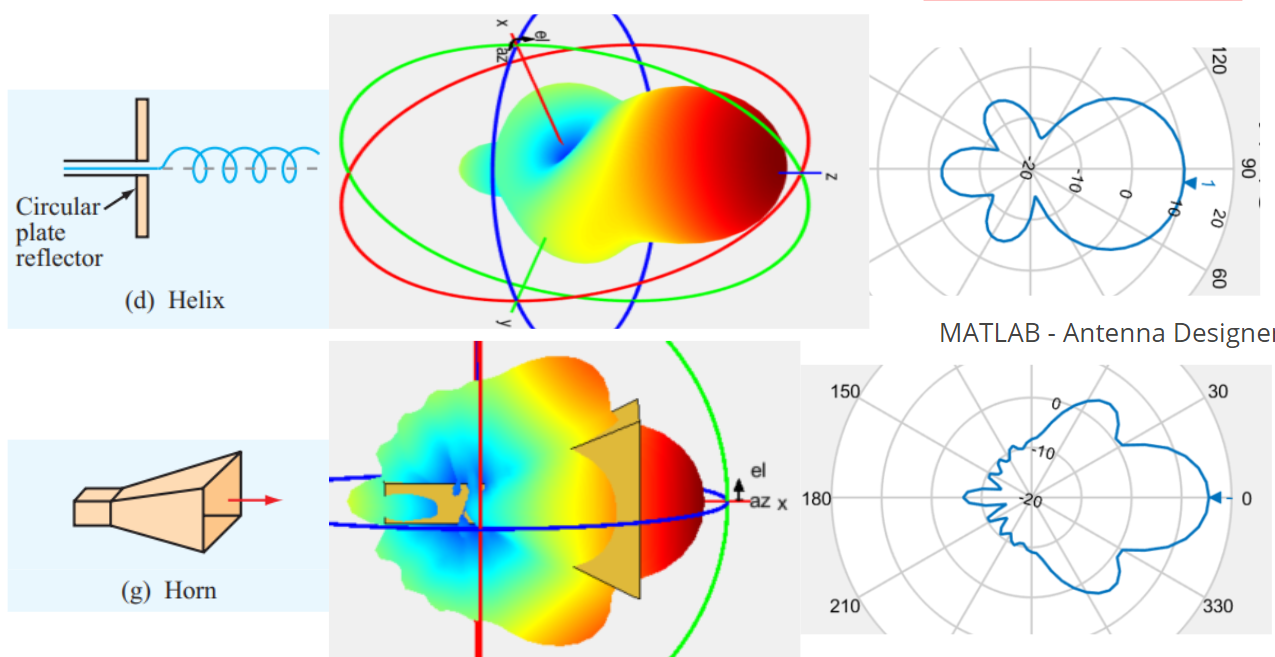
Using a software like MATLAB's Antenna Designer app, we obtain the radiation patterns of a dipole, a horn and helix antenna:
Voltage and current distributions, 2D and 3D radiation pattern of dipole antenna
3D and 2D radiation pattern of helix and horn antennas
As shown, for each antenna there is a corresponding radiation pattern associated with it. The dipole antenna has its characteristic omnidirectional pattern while the helix and horn have a pointier pattern with higher directivity at boresight. Very little can be done to change the radiation pattern of these antennas, a constraint that is present for every antenna used singularly. Phased-array antennas can alleviate this constraint and provide versatility in the radiation pattern.
The physical principle behind a versatile radiation pattern is wave interference. The interference phenomena in waves was discovered a long time ago and is no novel concept in the field. However, as with many other fields in engineering, the recent advances in mixed-signal hardware and novel digital signal processing (DSP) algorithms have allowed for the cost effective closed-loop implementation of phased-array antennas. Without these improvements the implementation of phased-array antennas was limited to complex and mostly analog systems such as the AN/FPS-85 Phased Array Radar facility in Florida.
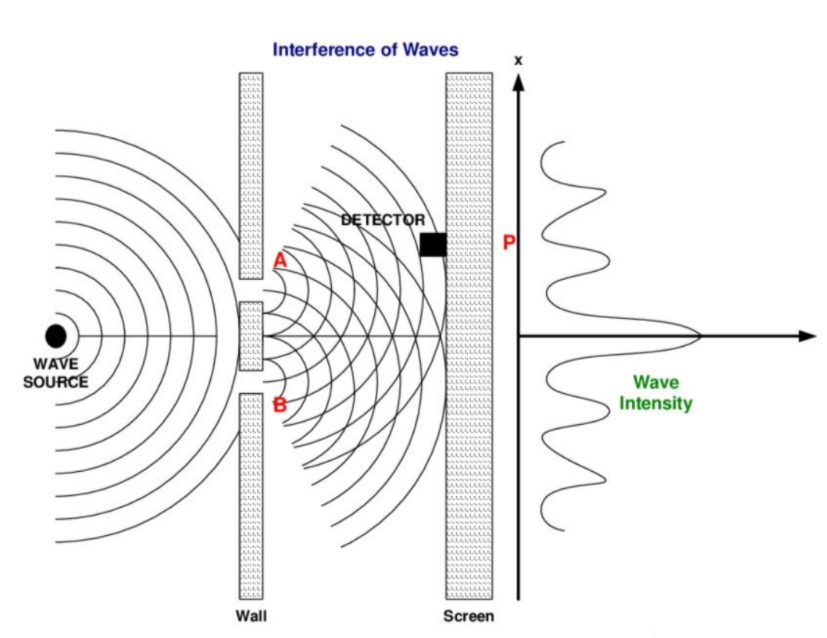
Recall from the double slit experiment that due to constructive and destructive interference of waves, the resulting wave intensity pattern of two isotropic wave sources resembles the amplitude of a sinc function.
Double-slit experiment illustrating the interference phenomena
Exploiting this concept with antennas and applying the pattern multiplication principle, we can theoretically analyze the performance of any array with the Array Pattern (Fa or AF), and treating the antennas as isotropic. Multiplying the Element Pattern, Fe (shown above for dipoles, helix and horn antennas) at the end results in the total radiation pattern.
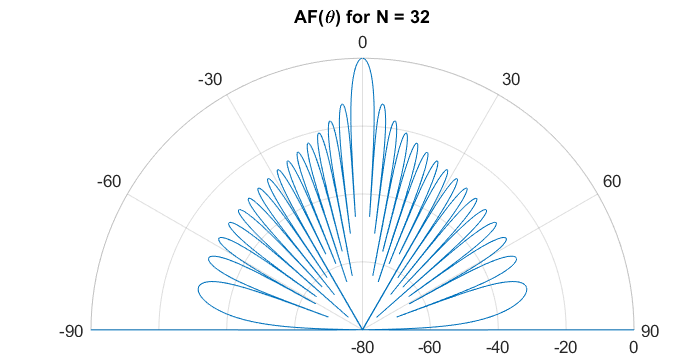
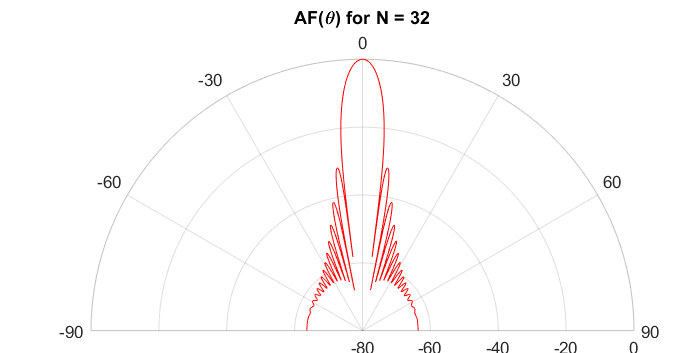
For an antenna array with uniform amplitude weights and no phase differences between neighbouring elements, the resultant radiation pattern is the magnitude of a sinc function, shown in polar coordinates below:
Main lobe at boresight and first side lobes at -13 dB.
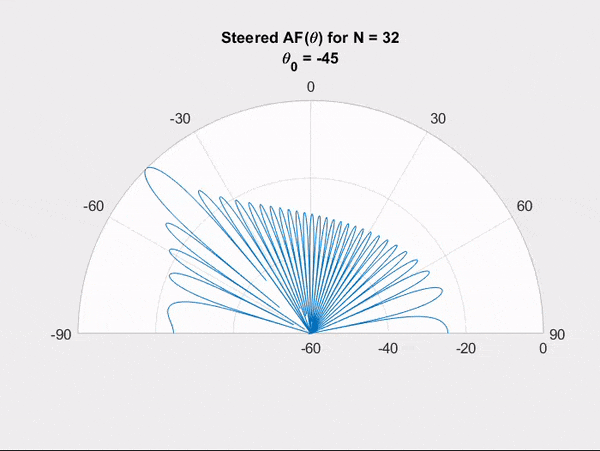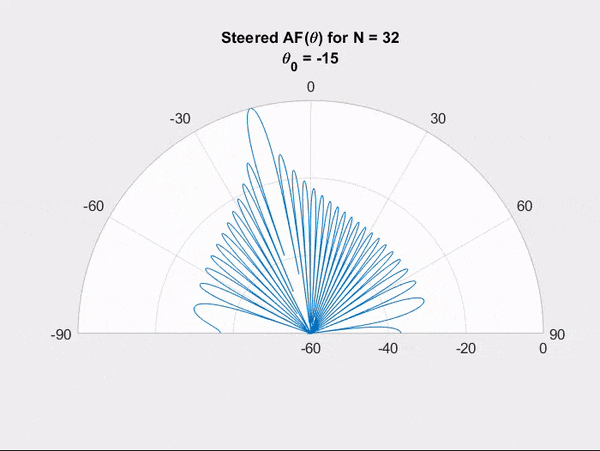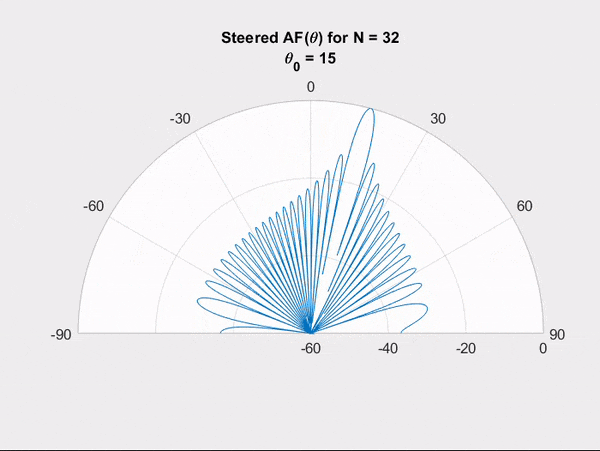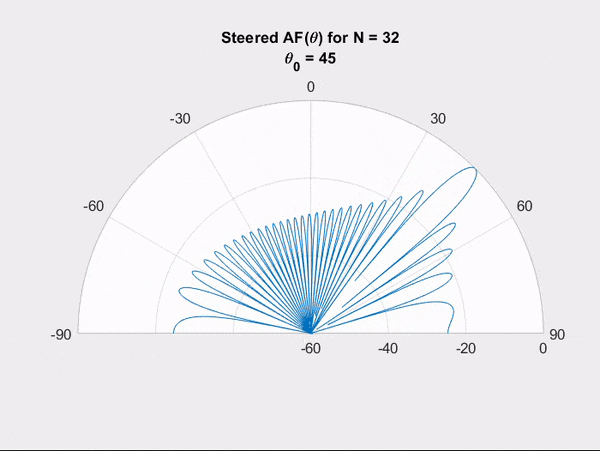
IC phase shifters or true-time delay circuits can be used to control the relative phase of each antenna with respect to its neighbours. With the idea of wave interference in mind, we can visualize how controlling the relative phase of the antennas can result in steering the main beam to a desired direction.
The ability to electronically steer an array is quite desirable as it eliminates the need to mechanically steer an antenna to change its beam's direction. In addition, electronic steering allows beam scanning at very fast rates.
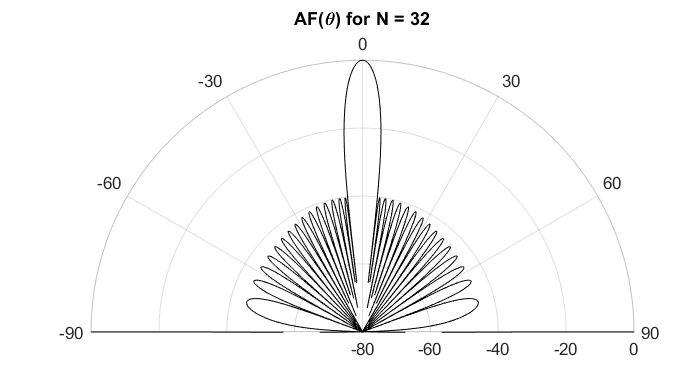
Steering can be achieved with phase-shifters, but the shape remained practically the same. Here we show how controlling the amplitude weights of the antenna elements can result in changes in the shape of the radiation pattern.
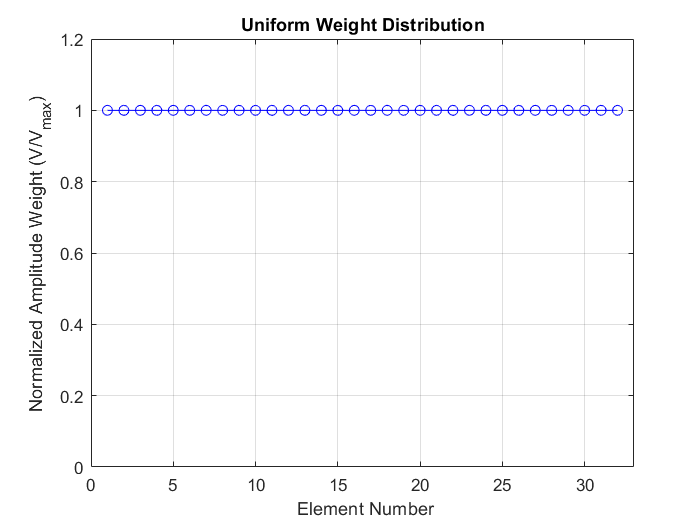
As mentioned above, the radiation pattern shown assumed a uniform weight distribution on all the antennas:
Radiation pattern in polar coordinates from a uniform weight distribution
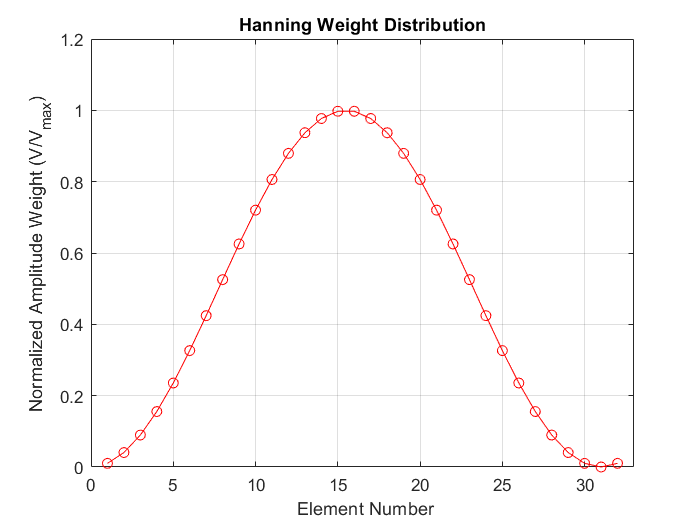
If instead of a uniform weight distribution, we apply a Hanning distribution following the equation,
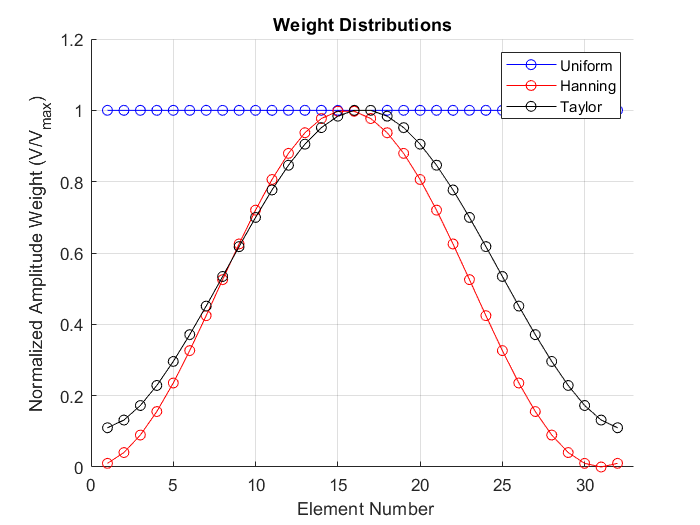
the antennas in the center of the array would receive stronger signals than the antennas at the edges. We can predict a pattern with a pointier profile, as shown.
Radiation pattern in polar coordinates from a Hanning weight distribution.
Applying a Hanning weight distribution will provide a much higher directivity and the power dissipated in the side lobes will be significantly reduced.
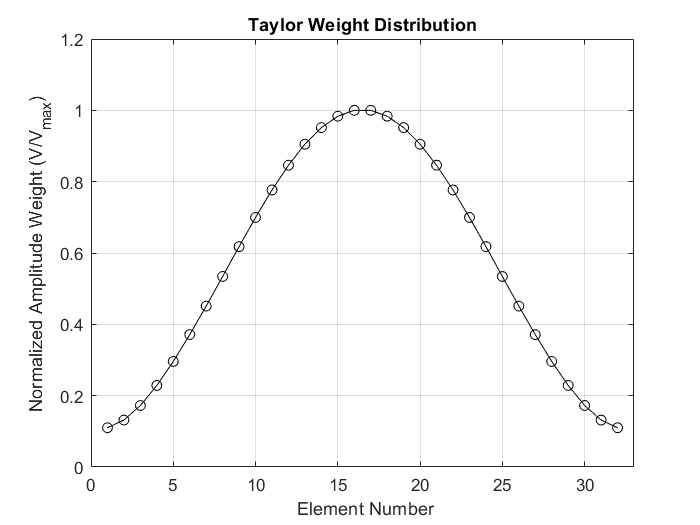
Implementing the Hanning weight distribution, however, is not easily realizable. Instead, a taylor distribution function is commonly used. This DSP algorithm can be accessed via multiple sources. In MATLAB, the function taylorwin(N, nbar, sll) returns a weight distribution for N elements, sll, the desired dB level of nearest sidelobes, and nbar the number of nearest side lobs with the sll value.
Radiation pattern in polar coordinates from the Taylor weight distribution, taylorwin(32, 6, -40)
With a similar weight distribution as with the Hanning function, the shape of the radiation pattern has a slightly different profile, but the same desired characteristic: lower side lobe levels.
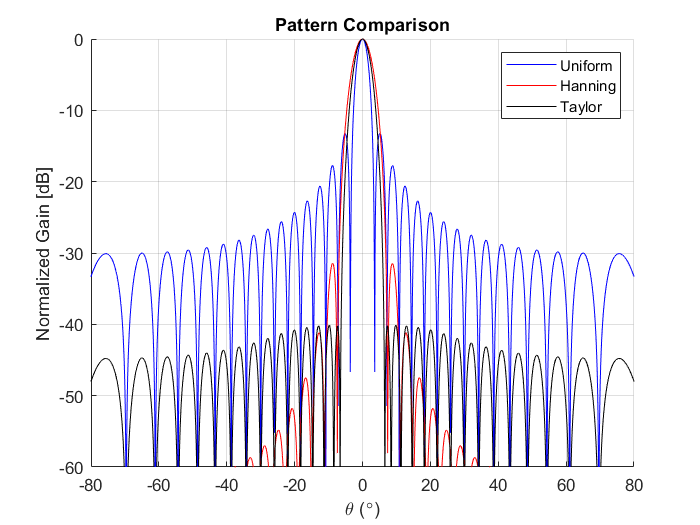
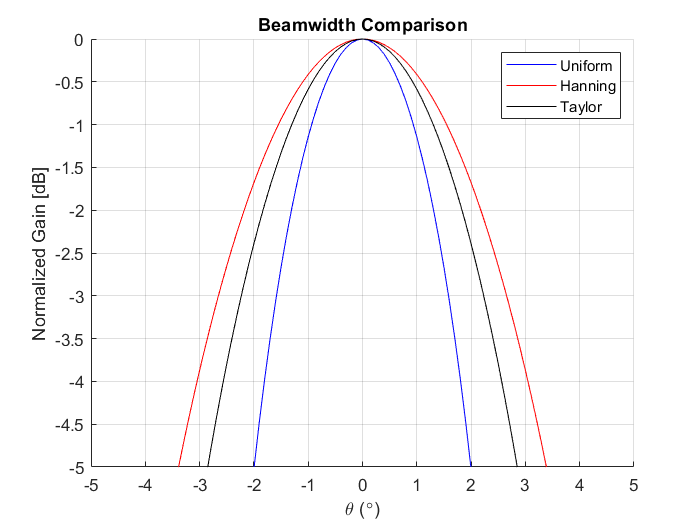
Comparing the three weight distributions, we see the differences in the radiation patterns and the main beamwidth. Depending on the constraints of the application, the widening of the beamwidth might need to be considered as a design parameter. In either case, controlling the weights of the signals feeding the individual antennas can provide a variety of desired radiation patterns depending on the application.
Comparison between Uniform, Hanning and Taylor Weight Distributions.
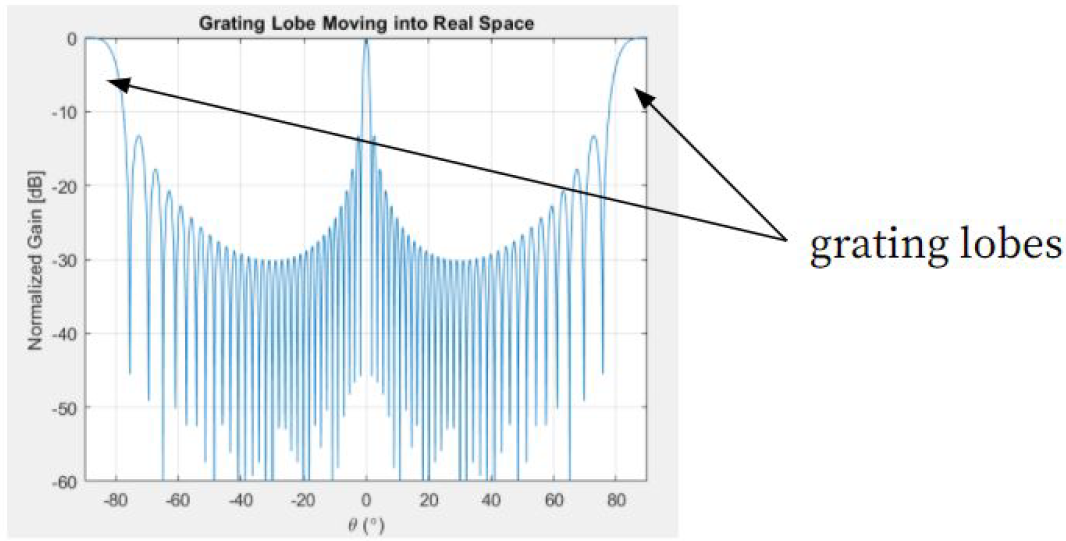
As with any other featured technology, there are always tradeoffs one should be aware of and manage well. The versatility in direction and shape of phased-array antennas do not come with zero costs. Grating lobes, as shown below, are unwanted and sometimes present in phased-array antennas due to signal aliasing. Grating lobes are not found in individual antennas as they are a consequence of array arrangements.
Analogously to the Nyquist theorem (or sampling theorem) in the time domain, which states that the sampling frequency needed to reproduce an incoming signal must be at least 2 times higher than the frequency of the signal, space aliasing can occur if antenna elements are placed too far or too close together with respect to the wavelength of the signal. To avoid grating lobes in a linear array, the distance between neighboring antennas should be between half and a full wavelength,
showcasing the duality between the space and time domains.
It is worth mentioning that phased-array antennas are at the heart of 5G and Internet of Things (IoT) technologies. In addition to the versatility highlighted in this text, phased-array antennas support massive MIMO (multiple-input, multiple-out) communication capabilities. These antennas are also highly present in the new upcoming mmWave architectures, with great companies investing large amounts of resources and time in research and development of phased-array antennas. Phased-array antennas are providing a great architecture for the advancement in communication systems.
In this repository, there are two scripts to perform linear phased-array simulations:
PhasedArraySineFunction.mPhasedArraySeriesFunction.m
In the first script, the Array Factor (AF) or Array Pattern (Fa) is assumed to be:
Provided the weight and phase distributions are uniform and linear respectively.
In the second script, the more general expression is used instead in order to simulate the shaping of the beam via non-uniform weighting functions.
For a textbook type reference on phased array antennas, I keep a copy of Ulaby's and Ravaioli's text "Fundamentals of Applied Electromagnetics." In this text the mathematical derivation is shown from first principles.
Another good resource on phased-array antennas is the three-part series of articles by IC engineers at Analog Devices Inc.