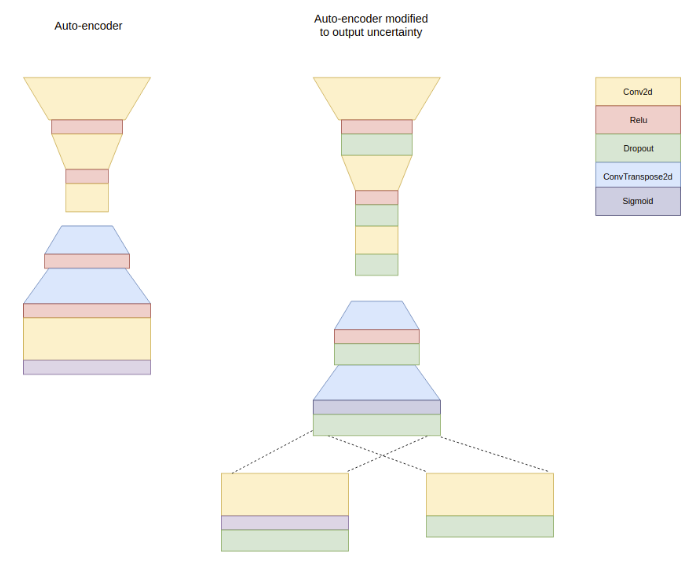
This repo can be seen as a simple implementation of Estimating the Mean and Variance of the Target Probability Distribution, and also a pytorch version of https://colab.research.google.com/github/stoerr/machinelearning-tensorflow/blob/master/published/PredictVariability.ipynb#scrollTo=rBNsC3kFOnt_
This paper assumes that the output of a neural network is drawn from a Gaussian distribution. Therefore, mu and sigma of the output can both be seen as functions of the output y, we can directly predict them as two variables.
regression.py splits the vector in the final dense layer. The predicted results of mu and sigma are shown in Figure1_split-at-dense.png.
regression2.py splits the vector at the very beginning, i.e. two networks with same structure but different parameters separately predict mu and sigma. The predicted results are shown in Figure2_split-at-begin.png.
I guess that regression.py works since mu and sigma are both functions of the output, therefore they may share some features. While in regression2.py, we see mu and sigma as two variables and train them separetely. Two results show no significant difference.
For other networks, I see an example in https://udion.github.io/post/uncertain_deepl/
And I also have a discussion with hmi88.