本实验是《数学建模导论:基于Python语言》的配套实验内容,马马将在这次实验中带大家一步步从小白到竞赛实战,让数学建模不再是一项可怕的竞赛。
在开始实验之前,大家可以先去anaconda官网安装python大礼包:www.anaconda.com
当然如果想安装原生Python也可以直接上python官网:www.python.org
但是Python如果是原生状态下的话里面啥都没有,所以如果碰到了库不存在的话,将命令行打开,键入pip install xxxx 能够解决大多数问题。 不过我想应该没有什么同学愿意为了节约一点表面上的空间去安装原生Python吧,不会吧不会吧?一如你去集贸的呷哺呷哺吃火锅你难道只会点一个锅底不点菜的吗? anaconda实际上就是提供锅底的同时还会提供你毛肚、鸭血、鸭肠等。所以,为什么不去安装一个anaconda呢?
如果觉得编程环境不好用的话可以加装一个VSCode或者Pycharm,但是华科的学生装正版Pycharm可能还有一点点问题因为学校邮箱出了点事。
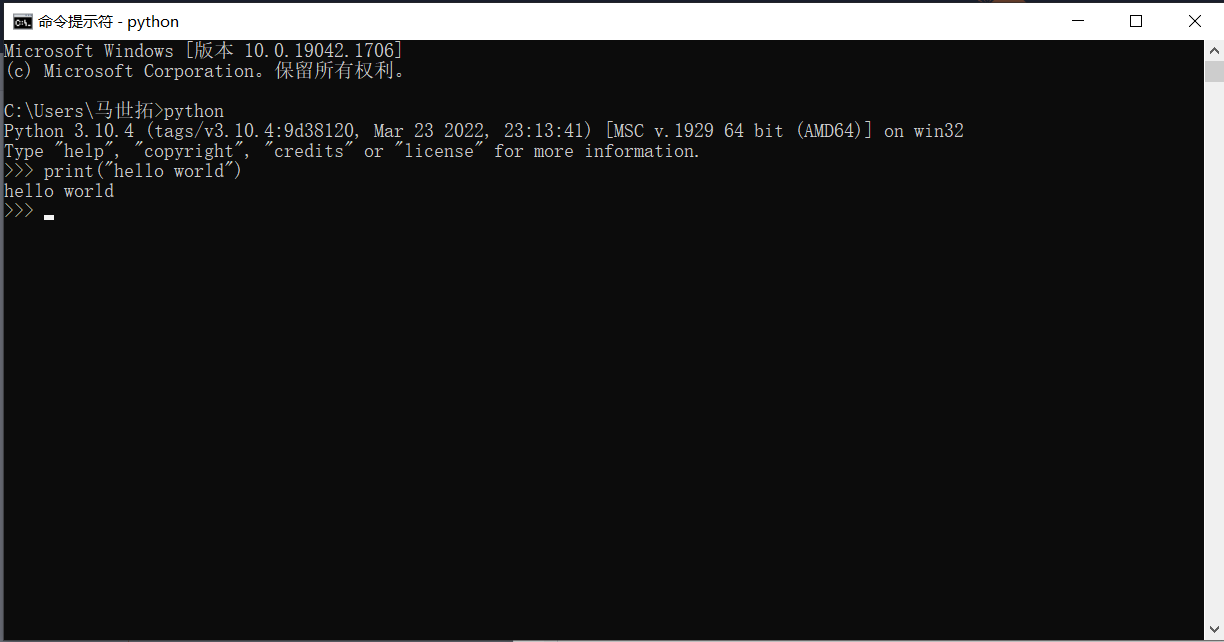
本次实验的基本目的是熟悉Python的基础语法。首先我们可以打开命令行(windows用户可以在cortana中键入cmd,会弹出命令提示符),然后键入python回车就可以切换到python命令行模式了。这一模式下我们可以试试它的hello world和C的hello world有多大差距:
可以看到Python的hello world仅需要一行。但是在更多情况下,我们和C一样会在文本文件中写程序然后运行。
这一次实验我们的目的就是熟悉基本的控制流和集合等内容。
现在对计算机1915班的前五名同学模电成绩想排个序,要求:
- 输入成绩个数为5,用input()函数实现
- 将输入的五个数保存成列表,并进行冒泡排序
- 不允许使用list自带的sort()方法,必须自己设置冒泡排序
- 将五个数排序后的结果排成一行输出到控制台
现在马马考完了模电,老师想在控制台里面根据我的成绩评价我的学习水平,要求:
- 控制台输入马马的模电分数
- 如果分数高于95,输出“马马+是卷王”;如果在80-95之间,输出“马马+牛牛”;如果在60-80之间,输出“马马+摆烂了”;如果低于60,输出“马马+老师,你不会又得重修了吧”
- 异常处理:如果分数是一个小于零的数或者输入的根本就不是数字如何handle?
老师手里有一份光之国模电考试的成绩单,保存成了txt文件,每一行分别是班里同学的名字和分数。现在需要:
- 利用open和read函数循环读取每一行,将结果保存到字典中
- 首先输出杰克、雷欧和贝利亚的模电成绩,如果检索不到人名需要报警“找不到这位同学”
- 然后循环遍历这个字典,对于每个同学的模电成绩按照第二关中的操作输出这位同学的状态
试着将第三关的语句改写为一个函数,函数参数为成绩单文件的路径与文件名。
本次实验的目的是为了熟悉基本的规划问题求解策略。求解规划问题需要用到numpy和scipy库,这两个库我建议先去熟悉一些基本操作会比较好。
这里我附上numpy和scipy的官方文档:
numpy官方文档:https://numpy.org/
scipy官方文档:https://scipy.org/
主要的方法就在scipy.optimize库当中,包括minimize、linear_sum_assignment等方法。
求这样一个线性规划的最优解:
求这样一个非线性规划的最优解,要求使用scipy.optimize.minimize求解:
现在光之国的五位奥特曼与阿布索留特族的五个小金人开始了1v1的车轮战,如果你现在安排奥特兄弟与他们1v1的战斗,每一项代表一个奥解决一个小金人所需要的时间。只有在最短的时间内打败所有小金人才能救出尤莉安公主。请问对于给定的小金人ABCDE,应该按照怎样的战斗策略使得五场战斗的时间总和最短?
| 奥特曼 | A | B | C | D | E |
|---|---|---|---|---|---|
| 佐菲 | 22 | 16 | 20 | 35 | 18 |
| 初代 | 20 | 12 | 35 | 40 | 26 |
| 赛文 | 11 | 19 | 15 | 17 | 21 |
| 杰克 | 25 | 30 | 21 | 37 | 40 |
| 艾斯 | 22 | 26 | 35 | 30 | 19 |
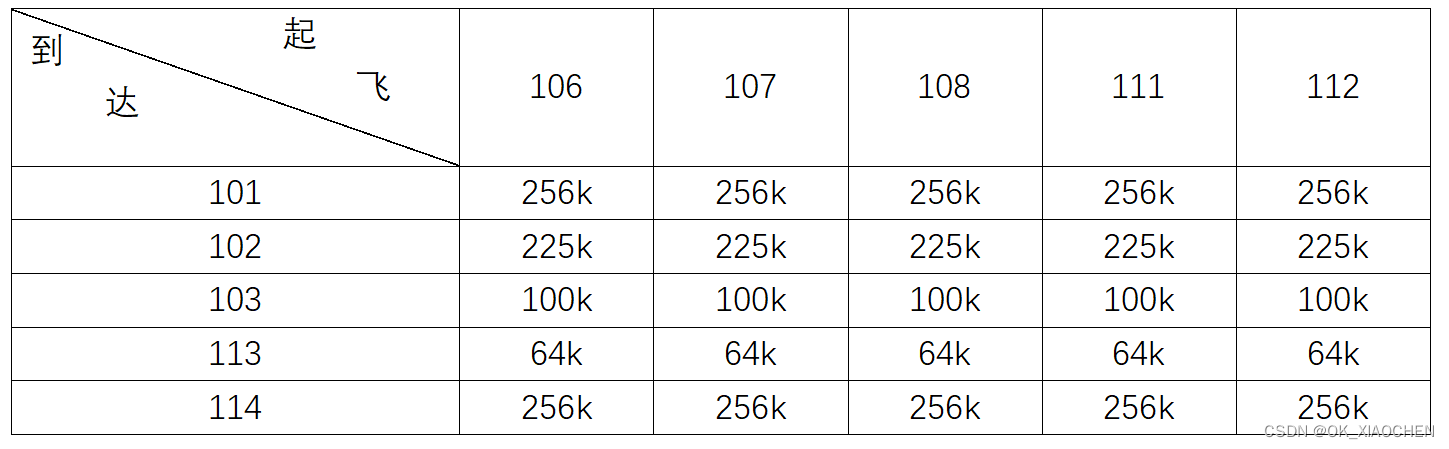
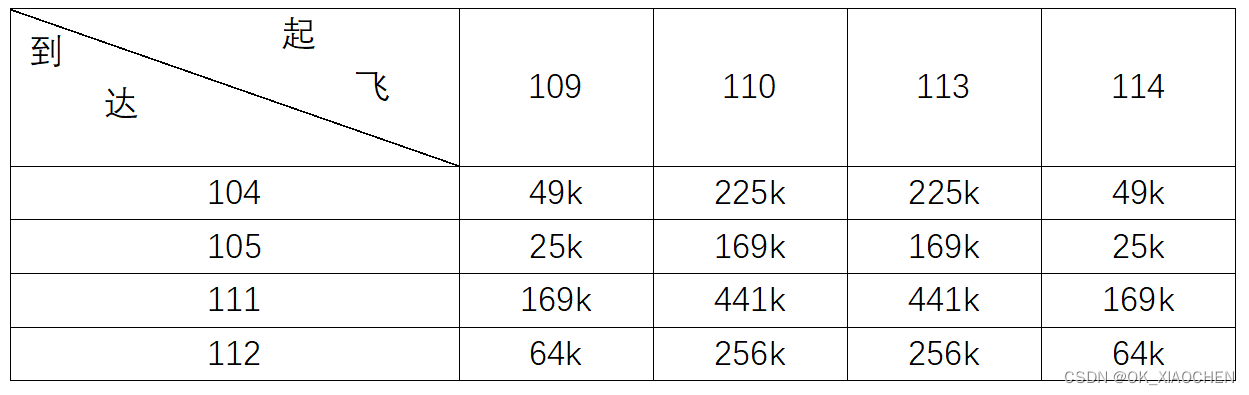
现在光之国开通了从M78星云(A)到L77星云(B)和U40(C)星云的宇宙航线,这些航线每天班次起飞与到达时间如下表。 设飞船在机场停留的损失费用大致与停留时间的平方成正比. 又每架飞船从降落到下班起飞至少需 2 小时准备时间, 试决定一个使停留费用损失为最小的分配飞行方案。
到M78星云损失费用:
到L77星云损失费用:
到U40星云损失费用:
对于问题四,写出你的分析思路,建立的模型表达式,程序和求解结果。最终形成一个不超过两页A4纸的文档。没啥格式要求,你认为你将你的思路表达清楚就够了。
本次实验的目的是对视频中讲到的微分方程模型进行进一步探究和补充。题目并不太多。
计算这样一个微分方程的符号解和数值解:y''-4y'+3y=x*exp(x),并且探究不同初值条件对数值解的影响
计算这样一个微分方程组的数值解:
三个方程定义了三维空间中的各个坐标点上度速度矢量,其中ρ、σ、β为常数,不同的参数可以算出不同的轨迹:x(t)、y(t)、z(t)。当参数为某些值时,轨迹出现混沌现象。即最小的初值差别也会显著地影响运动轨迹。
为了巩固经济增长基础、保障国内国际双循环,**政府已决定在全国进行 全人群的新冠病毒疫苗接种,以建立最大规模的国民群体新冠免疫屏障。但目前多地爆发二次疫情,在二次疫情中流行了一种名为“奥密克戎”的病毒。这种病毒是普通COVID-19效果的9-11倍,能在14秒之内使人感染,传播速度极快。对于某一个城市而言,请考虑这样一些问题:
- 目前疫苗对“奥密克戎”病毒并无免疫作用,现在考虑在没有对“奥密克戎”有效疫苗的情况下病毒的传播情况。
- 若现在已经研制出针对“奥密克戎”的疫苗,并且接种以后就可以不被感染,讨论在这一情况下某个城市内“奥密克戎”的传播情况。
- 事实上,疫苗并不能保证接种后不被感染,而是降低其感染后危重症的概率和死亡率,那么讨论在这一情况下病毒传播的效果。
- 以任意一个城市为例,考虑采取怎样的步骤、需要多大成本、多长时间可完成群体免疫屏障的建立。
在白垩纪时期潜伏在地底的怪兽双尾怪和古墩是一对捕食者和被捕食者关系。白垩纪的某一天,美菲拉斯星人的飞船队从太空带来了2000只双尾怪和3000只古墩来地球。假设双尾怪和古墩每年生育率为0.004和0.006,古墩会以双尾怪为食,试着分析
- 设置不同的参数绘制古墩和双尾怪在1000年内的变化情况
- 试着画出古墩和双尾怪变化的相轨图
- 1972年的一天在东京K地区,潜伏在地底的一只古墩和双尾怪复活了并打败了杰克奥特曼。地球防卫军准备开发一枚浓缩核弹将东京K地区炸毁。这枚核弹的爆炸威力是100万吨TNT当量,假设采用U235作为核弹原料,请查找资料并分析在引爆核弹以后半径多少以外是安全的?并给出半径与放射强度之间的数学建模与仿真。
这次实验内容很简单,我会上传一份iris.csv,大家试着去对鸢尾花数据做数据预处理,包括数据的填充,min-max规约和z-score规约,然后尽可能画一些描述性统计图表。
这次实验内容就一个问题,但我希望各位能用不同的方法解决,并给出一些有意思的结论。
宇宙帝王莫尔德和宙达准备率领大军攻打光之国,在此之前他们通过黑客技术从宇宙警备队科学局偷到了奥特六兄弟的资料。他们选取了一系列重要的评价指标对奥特兄弟的战力进行评估:
| 身高/m | 体重/t | 速度/马赫 | 年龄/** | 光线杀伤力 | 腕力/万吨 | 光线技能 | |
|---|---|---|---|---|---|---|---|
| 炎头队长 | 45 | 45000 | 10 | 2.5 | 1000 | 16 | M87光线 |
| 硫酸脸 | 40 | 35000 | 5 | 2 | 800 | 4 | 斯派修姆光线 |
| 莫西干 | 40 | 35000 | 7 | 1.7 | 750 | 5 | 艾梅丽姆光线 |
| 致敬 | 40 | 35000 | 6 | 1.7 | 850 | 12 | 希拉奈玛光线 |
| 肉联厂主任 | 40 | 45000 | 20 | 1.5 | 900 | 14 | 梅塔利姆光线 |
| 太子爷 | 53 | 55000 | 20 | 1.2 | 1000 | 16 | 斯托里姆光线 |
请对六位奥特曼的能力进行评估,你认为谁最难搞定?如果安排车轮战,消耗顺序应该是怎样的?

这一节的实验我们希望能够通过对2022美赛C题比特币价格预测问题的求解,熟悉arima模型的编程细节。
根据附件Bitcoin.csv,预测比特币在未来30日内的收盘价变化。

这一节的实验包括单向最短路径问题和TSP问题的求解,其中TSP问题的求解建议使用遗传算法求解,如果使用动态规划也是可以的。如果不太熟悉遗传算法的同学可以参考第八章。

我知道这个问题你们手算都可以算出来,我希望你们能够用Floyd和Dijsktra两种算法进行计算。
这里我可以给出34个城市的坐标,希望能够求解一条路径,它能不重复走完34个城市,然后总的路径长是最短的。

| 经度 | 纬度 |
|---|---|
| 116.46 | 39.92 |
| 117.2 | 39.13 |
| 121.48 | 31.22 |
| 106.54 | 29.59 |
| 91.11 | 29.97 |
| 87.68 | 43.77 |
| 106.27 | 38.47 |
| 111.65 | 40.82 |
| 108.33 | 22.84 |
| 126.63 | 45.75 |
| 125.35 | 43.88 |
| 123.38 | 41.8 |
| 114.48 | 38.03 |
| 112.53 | 37.87 |
| 101.74 | 36.56 |
| 117 | 36.65 |
| 113.6 | 34.76 |
| 118.78 | 32.04 |
| 117.27 | 31.86 |
| 120.19 | 30.26 |
| 119.3 | 26.08 |
| 115.89 | 28.68 |
| 113 | 28.21 |
| 114.31 | 30.52 |
| 113.23 | 23.16 |
| 121.5 | 25.05 |
| 110.35 | 20.02 |
| 103.73 | 36.03 |
| 108.95 | 34.27 |
| 104.06 | 30.67 |
| 106.71 | 26.57 |
| 102.73 | 25.04 |
| 114.1 | 22.2 |
| 113.33 | 22.13 |
这一实验我们基于实验六对比特币的预测,分析比特币和黄金股价,如果每一次投资都必须至少经过一周才能重新调仓,在你有十万美金的前提下应该如何安排每次的投资策略才能在五年后盈利最大?
对于附件中提供的iris.csv(也可以通过sklearn.datasets去load_iris()),对其进行以下基本操作:
尽可能想到更多的可视化表现形式,绘制成图表并附带文字描述
对于鸢尾花的数据,分析每个特征对鸢尾花类别的影响,你认为用怎样的假设检验去分析最为合适?
尝试利用不同的分类器去分类鸢尾花数据,并将结果用不同的衡量指标或可视化图表表示。
尝试使用Kmeans聚类方法去对鸢尾花进行聚类,并利用轮廓系数等方法测量K最优的取值。
与实验九对应,可以使用sklearn.datasets.load_boston()获取波士顿房价数据集进行预测。这里我们更多的是做回归分析。
尽可能想到更多的可视化表现形式,绘制成图表并附带文字描述
对于房价的数据,分析每个特征对房价类别的影响,你认为用怎样的假设检验去分析最为合适?能否建立这些量之间的回归方程并进行检验?
尝试利用不同的回归器去分类鸢尾花数据,并将结果用不同的衡量指标或可视化图表表示。
参考实验七的问题2中给出的34城市TSP问题,要求从遗传算法、蚁群算法、粒子群算法、模拟退火算法中至少选择两种进行实现。如果有更多的想法也欢迎使用你们看到的资料。
试着从网上查找资料,复现一个生命游戏的元胞自动机。这里我给出一个案例:
"""
元胞自动机 Python 实现
"""
import numpy as np
import matplotlib.pyplot as plt
class GameOfLife(object):
def __init__(self, cells_shape):
"""
Parameters
----------
cells_shape : 一个元组,表示画布的大小。
Examples
--------
建立一个高20,宽30的画布
game = GameOfLife((20, 30))
"""
# 矩阵的四周不参与运算
self.cells = np.zeros(cells_shape)
real_width = cells_shape[0] - 2
real_height = cells_shape[1] - 2
self.cells[1:-1, 1:-1] = np.random.randint(2, size=(real_width, real_height))
self.timer = 0
self.mask = np.ones(9)
self.mask[4] = 0
def update_state(self):
"""更新一次状态"""
buf = np.zeros(self.cells.shape)
cells = self.cells
for i in range(1, cells.shape[0] - 1):
for j in range(1, cells.shape[0] - 1):
# 计算该细胞周围的存活细胞数
neighbor = cells[i-1:i+2, j-1:j+2].reshape((-1, ))
neighbor_num = np.convolve(self.mask, neighbor, 'valid')[0]
if neighbor_num == 3:
buf[i, j] = 1
elif neighbor_num == 2:
buf[i, j] = cells[i, j]
else:
buf[i, j] = 0
self.cells = buf
self.timer += 1
def plot_state(self):
"""画出当前的状态"""
plt.title('Iter :{}'.format(self.timer))
plt.imshow(self.cells)
plt.show()
def update_and_plot(self, n_iter):
"""更新状态并画图
Parameters
----------
n_iter : 更新的轮数
"""
plt.ion()
for _ in range(n_iter):
plt.title('Iter :{}'.format(self.timer))
plt.imshow(self.cells)
self.update_state()
plt.pause(0.2)
plt.ioff()
if __name__ == '__main__':
game = GameOfLife(cells_shape=(60, 60))
game.update_and_plot(200)