Custom matlab snr function for accepting only 1 harmonic, accepting given target frequency, accepting exclude PSDs below a given frequency from computing noise power forcely.
The following codes could be found in example_matlab.m
-
Generate a signal
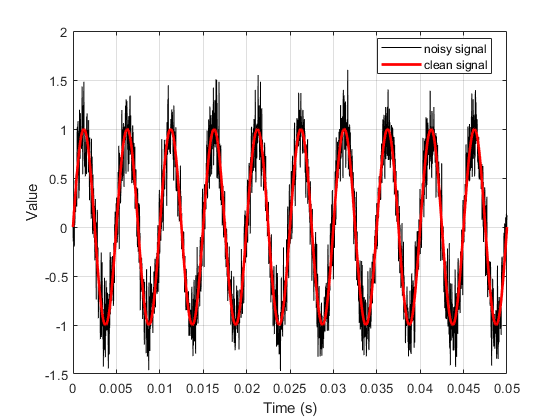
rng(111); % reproducability fs = 4e4; % sampling rate in Hz t = 0:1/fs:0.05; % sampled time points %% mono frequency sinusidal signal disp('generating mono frequency signal...') target_frequency = 200; % Hz s1_clean = sin(2*pi*target_frequency*t); % add noise target_snr = 10; s1 = awgn(s1_clean, target_snr, 'measured'); % display signal in time domain figure; plot(t, s1, 'k', 'DisplayName', 'noisy signal'); hold on grid on plot(t, s1_clean, 'r', 'LineWidth', 2, 'DisplayName', 'clean signal'); legend('Location', 'best'); xlabel('Time (s)') ylabel('Value')
-
Count snr
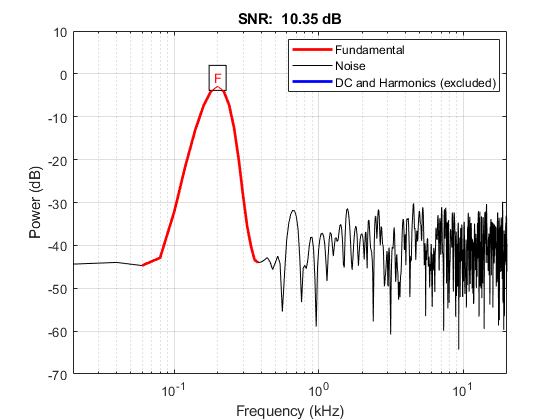
% 1 harmonic, given target frequency number_harmonic = 1; % snr(s1, fs, number_harmonic); custom_matlab_snr(s1, fs, number_harmonic, target_frequency); [snr_s1, noise_power_s1] = custom_matlab_snr(s1, fs, number_harmonic, ... target_frequency); fprintf('SNR with 1 harmonic: %.4f\n', snr_s1)
-
Count snr, but exclude low frequency response from counting noise power.
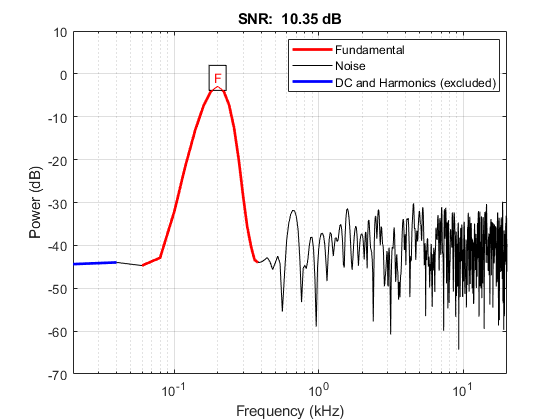
% 1 harmonic, given target freuency, exclude psd below 300 Hz when counting % noise power max_frequency_dc = target_frequency; % Hz custom_matlab_snr(s1, fs, number_harmonic, target_frequency, max_frequency_dc); [snr_s1_dc, noise_power_s1_dc] = custom_matlab_snr(s1, fs, number_harmonic, ... target_frequency, max_frequency_dc); fprintf('SNR with 1 harmonic and force DC: %.4f\n', snr_s1_dc)
-
Compared with snr results counting from time domain:
% matlab snr from time domain results snr_s1_t = snr(s1, s1-s1_clean); fprintf('SNR from time domian: %.4f\n', snr_s1_t)
output:
generating mono frequency signal... SNR with 1 harmonic: 10.3464 SNR with 1 harmonic and force DC: 10.3464 SNR from time domian: 10.4806
-
Generate a signal
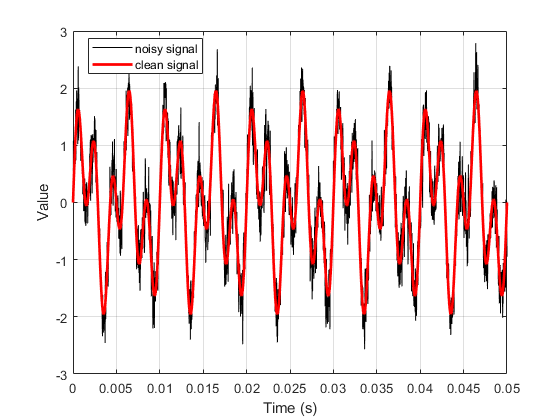
%% multi frequency disp('generating dual frequency signal...') target_frequency2 = 500; % Hz s2_clean = s1_clean + sin(2*pi*target_frequency2*t); % add nosie s2 = awgn(s2_clean, target_snr, 'measured'); % display signal in time domain figure; plot(t, s2, 'k', 'DisplayName', 'noisy signal'); hold on grid on plot(t, s2_clean, 'r', 'LineWidth', 2, 'DisplayName', 'clean signal'); legend('Location', 'best'); xlabel('Time (s)') ylabel('Value')
-
Count snr
- frequency 1:
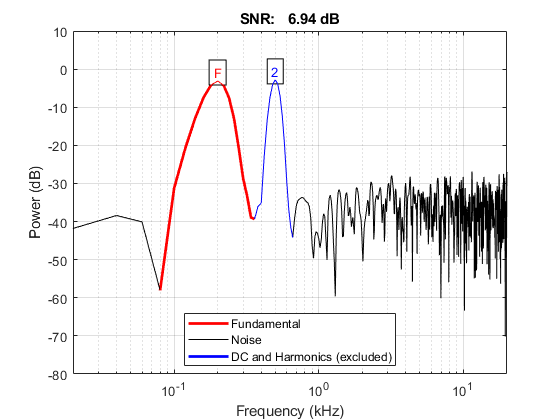
% 1 harmonic, given target frequencies disp('1 harmonic:') % frequency 1 % snr(s2, fs, number_harmonic); custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency, target_frequency2]); % signal power of 2nd frequency % will be excluded from counting noise power (By marking it as 2nd Harmonic) [snr_s21, noise_power_s21] = custom_matlab_snr(s2, fs, number_harmonic,... [target_frequency, target_frequency2]);
- frequency 2:
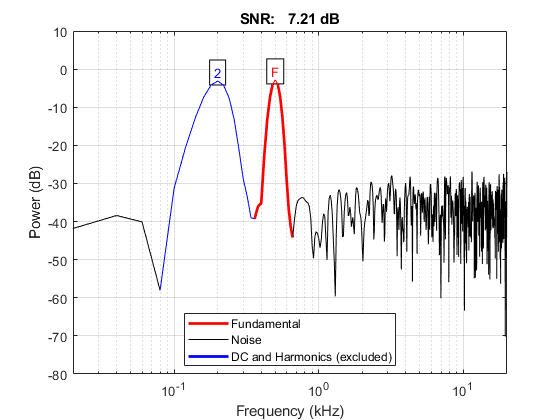
custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency2, target_frequency]); % move target frequency to be first [snr_s22, noise_power_s22] = custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency2, target_frequency]);
- overall snr:
% overall snr snr_s2 = mean([snr_s21, snr_s22]); fprintf('SNR:\n\tOverall(mean): %.4f dB\n\t%d Hz: %.4f dB\n\t%d Hz: %.4f dB\n',... snr_s2, target_frequency, snr_s21, target_frequency2, snr_s22); fprintf('\tOverall(sqrt sum square): %.4f dB\n',... sqrt((snr_s21^2+snr_s22^2)))
output:
generating dual frequency signal... 1 harmonic: SNR: Overall(mean): 7.0789 dB 200 Hz: 6.9433 dB 500 Hz: 7.2145 dB Overall(sqrt sum square): 10.0129 dB -
Count snr, but exclude low frequency response from counting noise power.
- frequency 1:
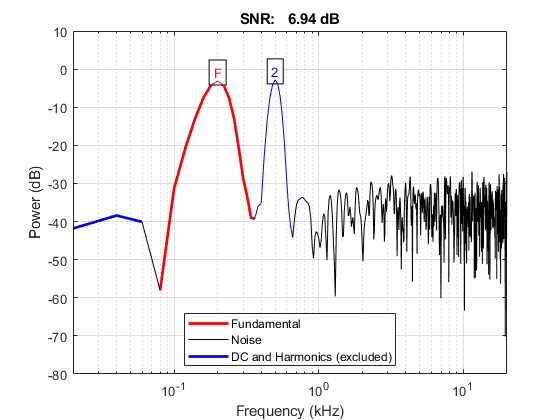
% 1 harmonic, given target freuency, exclude psd below 200 Hz when counting % noise power disp('1 harmonic, exclude psd below 200 Hz when counting noise power:') max_frequency_dc = target_frequency; % Hz % frequency 1 custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency, target_frequency2], max_frequency_dc); [snr_s23, noise_power_s23] = custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency, target_frequency2], max_frequency_dc);
- frequency 2:
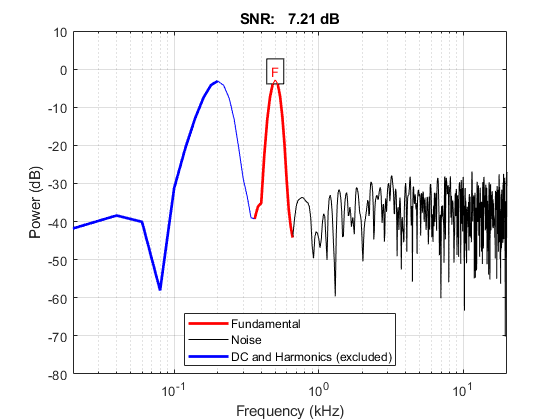
% frequency 2 custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency2, target_frequency], max_frequency_dc); [snr_s24, noise_power_s24] = custom_matlab_snr(s2, fs, number_harmonic, ... [target_frequency2, target_frequency], max_frequency_dc);
- overall snr:
snr_s2_c = mean([snr_s23, snr_s24]); fprintf('SNR:\n\tOverall(mean): %.4f dB\n\t%d Hz: %.4f dB\n\t%d Hz: %.4f dB\n',... snr_s2_c, target_frequency, snr_s23, target_frequency2, snr_s24); fprint f('\tOverall(sqrt sum square): %.4f dB\n',... sqrt((snr_s23^2+snr_s24^2)))
output:
1 harmonic, exclude psd below 200 Hz when counting noise power: SNR: Overall(mean): 7.0786 dB 200 Hz: 6.9430 dB 500 Hz: 7.2142 dB Overall(sqrt sum square): 10.0125 dB -
Compared with snr results counting from time domain:
% matlab snr from time domain results snr_s2_t = snr(s2, s2-s2_clean); fprintf('SNR from time domian: %.4f\n', snr_s2_t)
output:
SNR from time domian: 10.3977
The following codes could be found in custom_matlab_snr.py
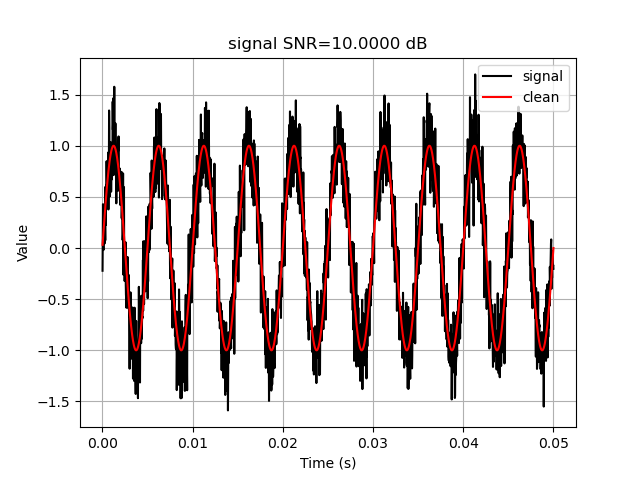
print('generating mono frequency signal...')
fs = 4e4
t = np.arange(1/fs, 0.05, 1/fs) # seconds
f = 200
clean = np.sin(2 * np.pi * f * t)
np.random.seed(111) # reproducability
def awgn(s, snr):
# https://stackoverflow.com/a/53688043
# https://www.cnblogs.com/skykill/p/7474136.html
# Convert to linear Watt units
ps_vs_pn = 10 ** (snr / 10)
signal_power = np.sum(s ** 2) / len(s)
nosie_power = signal_power / ps_vs_pn
# Generate noise samples
mean_noise = 0
noise = np.random.normal(
mean_noise, np.sqrt(nosie_power), len(s))
return s + noise
target_snr = 10 # dB
signal = awgn(clean, target_snr)
plt.plot(t, signal, c='k', label='signal')
plt.plot(t, clean, c='r', label='clean')
plt.xlabel('Time (s)')
plt.ylabel(r'Value')
plt.title(f'signal SNR={target_snr :.4f} dB')
plt.legend()
plt.grid()
plt.show()
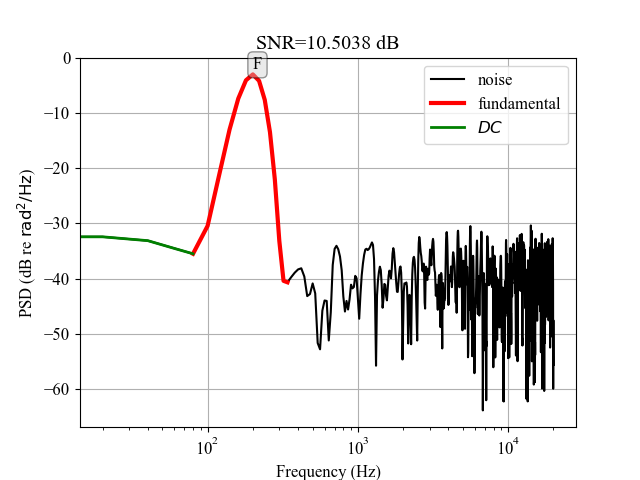
all_snr = snr_helper(
waveform=np.reshape(signal, [1, -1]),
sampleRate=fs,
numberHarmonics=1,
targetFrequency=np.ones([1, 1]) * f,
isPlot=True,
isLogScale=True
)
print(f'snr of 1 harmonic: {all_snr[0, 0]} dB')
# snr from time domain
snr_t = 10 * np.log10(
(np.sum(signal ** 2) / len(signal)) /
(np.sum((signal-clean) ** 2) / len(signal))
)
print(f'SNR from time domain: {snr_t:.4f} dB')
# dual frequency
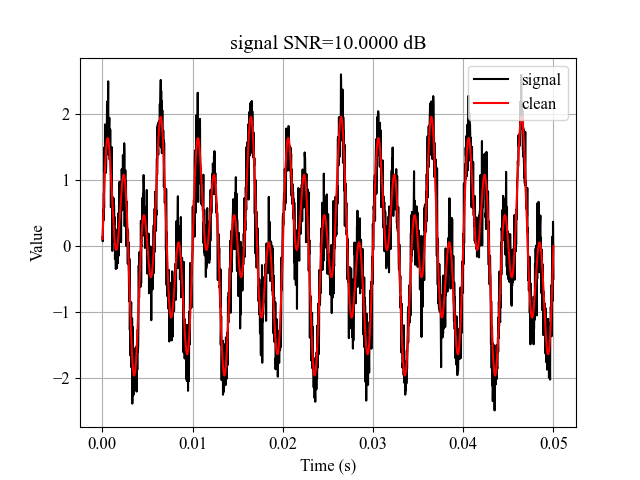
print('generating dual frequency signal...')
f2 = 500
clean2 = np.sin(2 * np.pi * f2 * t) + clean
signal2 = awgn(clean2, target_snr)
plt.plot(t, signal2, c='k', label='signal')
plt.plot(t, clean2, c='r', label='clean')
plt.xlabel('Time (s)')
plt.ylabel(r'Value')
plt.title(f'signal SNR={target_snr :.4f} dB')
plt.legend()
plt.grid()
plt.show()
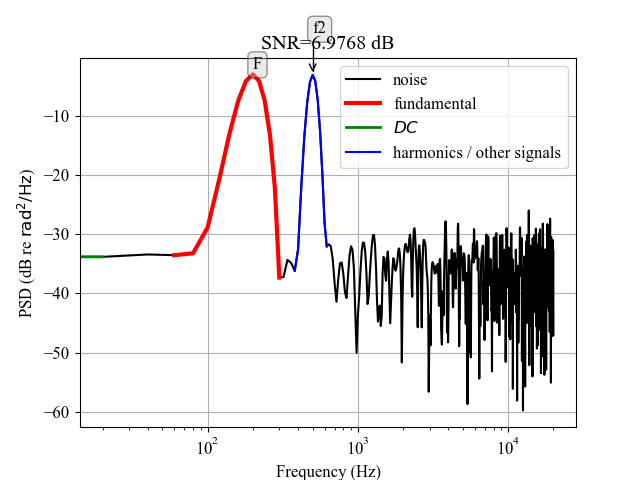
all_snr = snr_helper(
waveform=np.reshape(signal2, [1, -1]),
sampleRate=fs,
numberHarmonics=1,
targetFrequency=np.array([[f, f2]]),
isPlot=True,
isLogScale=True
)
mean_snr = np.mean(all_snr)
print(f'SNR:\n\toverall (mean): {mean_snr} dB'
f'\n\t{f} Hz: {all_snr[0, 0]} dB'
f'\n\t{f2} Hz: {all_snr[0, 1]} dB')
sqrt_sum_square_snr = np.sqrt(np.sum(np.square(all_snr)))
print(f'\toverall (sqrt sum square): {sqrt_sum_square_snr} dB')
# snr from time domain
snr_t = 10 * np.log10(
(np.sum(signal2 ** 2) / len(signal2)) /
(np.sum((signal2 - clean2) ** 2) / len(signal2))
)
print(f'SNR from time domain: {snr_t:.4f} dB')output:
generating mono frequency signal...
snr of 1 harmonic: 10.503775172600168 dB
SNR from time domain: 10.4778 dB
generating dual frequency signal...
SNR:
overall: 6.94580441953717 dB
200 Hz: 6.976787517223854 dB
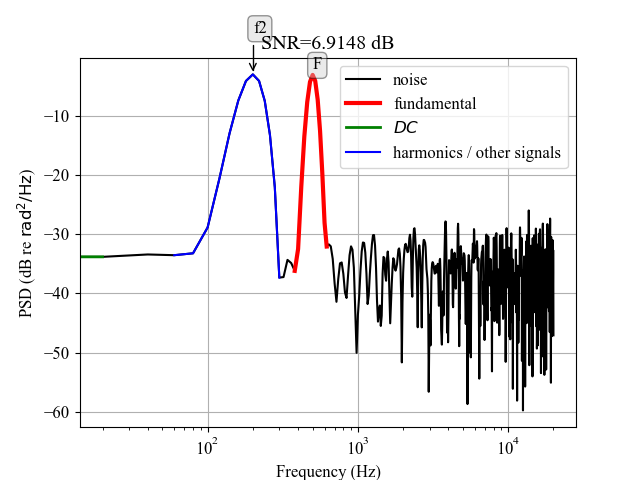
500 Hz: 6.9148213218504875 dB
overall (sqrt sum square): 9.822948537664681 dB
SNR from time domain: 10.5996 dB