It is a problem in which we need to complete a cycle passing through a set of points, being the distance between any pair of points known, without repeating any point and returning to the origin once all points have been visited.
A clear example is the Travelling Salesman Problem: Suppose there are several locations in a city that need to be visited, having the distances of every pair of points stored in a matrix. The objective is to complete the cycle following the optimal path, the one which minimize the traversed distance.
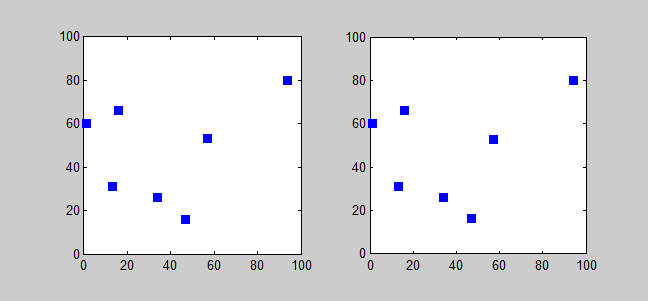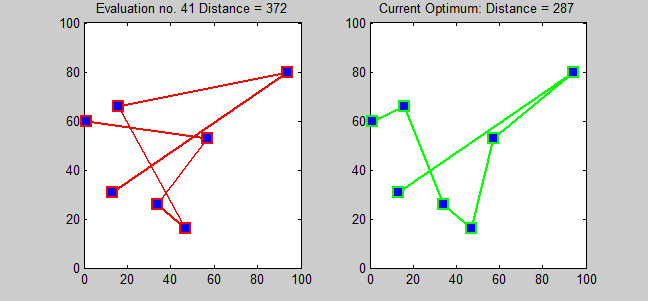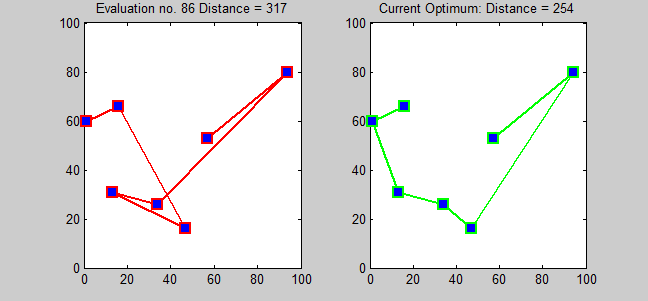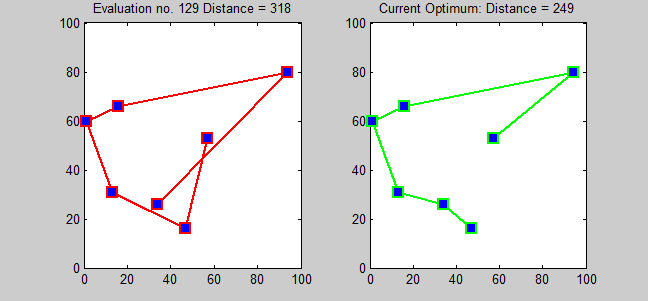
In order to solve this problem, I have used the Held-Karp algorithm.
The Held-Karp algorithm is a brute search algorithm which belong to the family of the "branch and bound" ones.
An algorithm that belongs to the Branch and bound family is used to solve problems where we could obtain an optimal solution given a set of possible solutions. The algorithm will evaluate all the possible alternatives, keeping the best one and using it as a threshold to improve.
This would be an example of the use of Held-Karp to this problem:
The repository contains an example of an input file, and 2 variants of the Held-Karp algorithm:
It is an example of a distance distance, where the different rows and columns refers to different locations. The main diagonal is always zero because the distance from one location to itself is always zero. Its important to know that the distance A-B could be different from the distance B-A.
First implementation of the algorithm, which allow us to see all the posibilities with their distances. It is less eficient than the next implementation, because it needs to store all the paths with their corresponding distances to print them at the end of the process.
Final implementation of the algorithm, which do not show all the possible routes, just the optimal one. It is more efficient than the previous implementation.
- It is important to recall that the distance A-B could be different from the distance B-A (imagine a one-way street, going in one direction is shorter that the opposite).
- It does not matter which is the starting point, because at the end the cycle will cover all the locations, the result would be the same starting at any other location.
- This problem needs big computational capacity. With each new location, the time to calculate the optimal solution increase exponentially (more than 12 locations could be a nightmare).