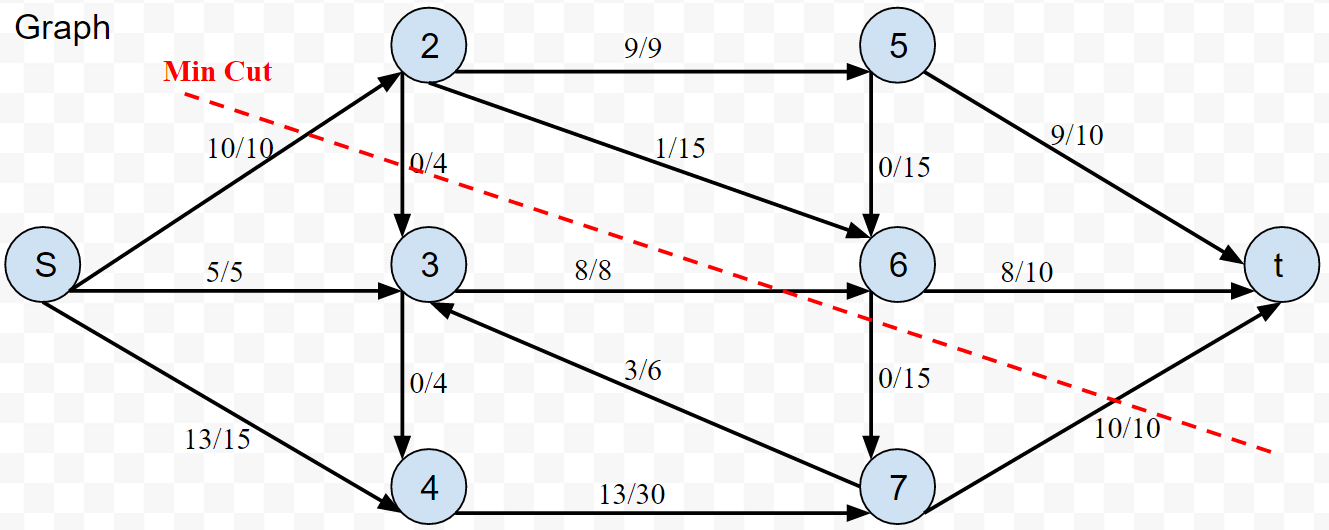
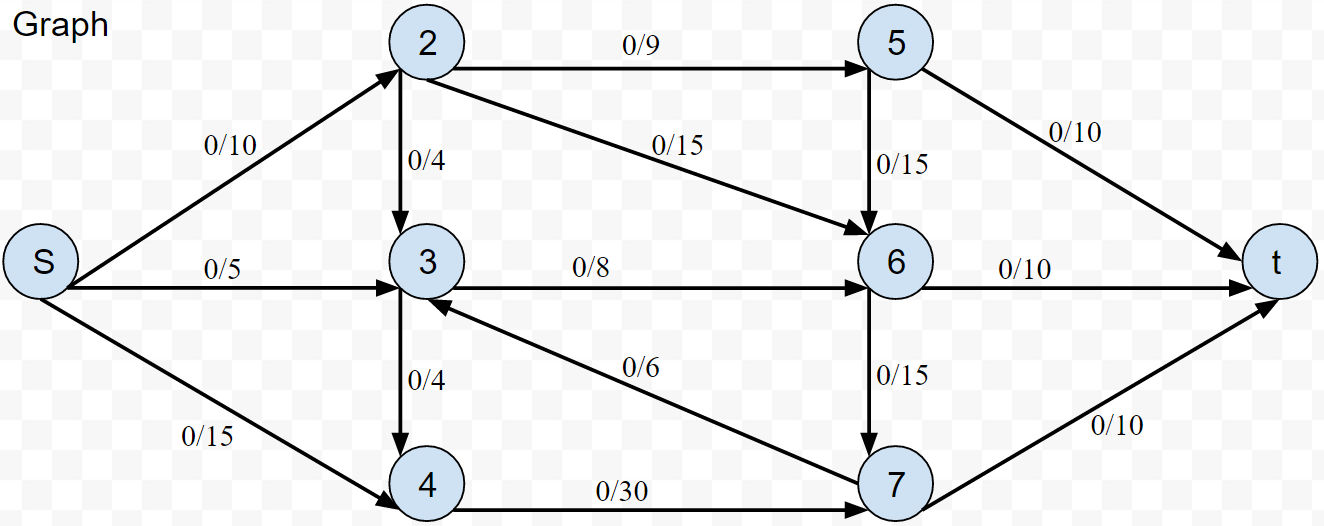
Ford Fulkerson Max-Flow / Min Cut Algorithm

Simple implementation to find the maximum flow through a flow network (no Capacity Scaling)

"0/10" means an edge with capacity 10 and 0 flow assigned

Terminology

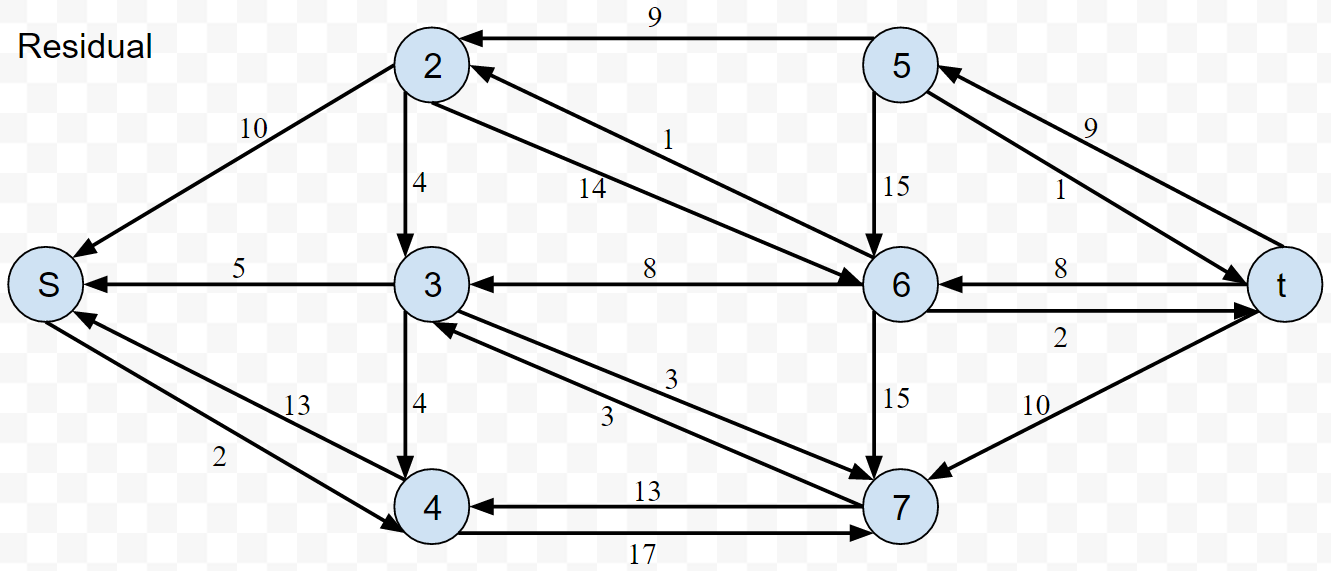
Residual graph
Directed graph showing how much of the flow assignments can be undone
Edge e=(u,v) shows how much flow is left to be assigned to that edge
Edge e=(v,u) is how much flow already been assigned (how much ca be undone)
Augmentation Path
An arbitrary path from S to T found in residual graph
Bottleneck
Minimum capacity from the path found in the residual graph (how much flow is assigned after each path is found)

vertexCount must be hard coded for different graphs
Code deals directly with integer array indexes. Index 0 is S (source) and index vertexCount-1 is T (sink) (-1 since arrays count from 0)
arrayIndexStringEquivalents holds string equivalents of the index. So vertices can have humanly readable IDs like S & T, and don't have to be sequential integers
- arrayIndexStringEquivalents[1] is 2 because the vertex called "2" is the in position 1 in the array indexes
Graphs are represented as adjacency matrices
- Directed Graph so order matters
- graphMatrix[i][j] represents the capacity of an edge from i to j
  - 0 if no edge exists
  - No vertex has an edge to itself. There should always be a 0 in graphMatrix[x][x]
    - graphMatrix[0][0] is 0 since S has no edges to itself
    - Same for all vertices
    - graphMatrix[1][1] is 0 since the vertex in position 1 (vertex "2") has no edges to itself, etc.
  - Row vertexCount-1 is always all 0's since T (the sink) has NO outgoing edges {0, 0, 0, 0, 0, 0, 0, 0}

Constructor takes in an array of strings to have human readable vertices instead of ints
maxFlow() finds the maximum flow through the network
- Creates a residual graph & leaves the original graph unchanged
Uses Breadth First Search bfs() to find augmentation paths
- Returns true/false if a path from S to T was found
- Updates parent[] array so the actual path can be found
maxFlow() outputs each augmentation path found & the amount of flow added to total flow (bottleneck)