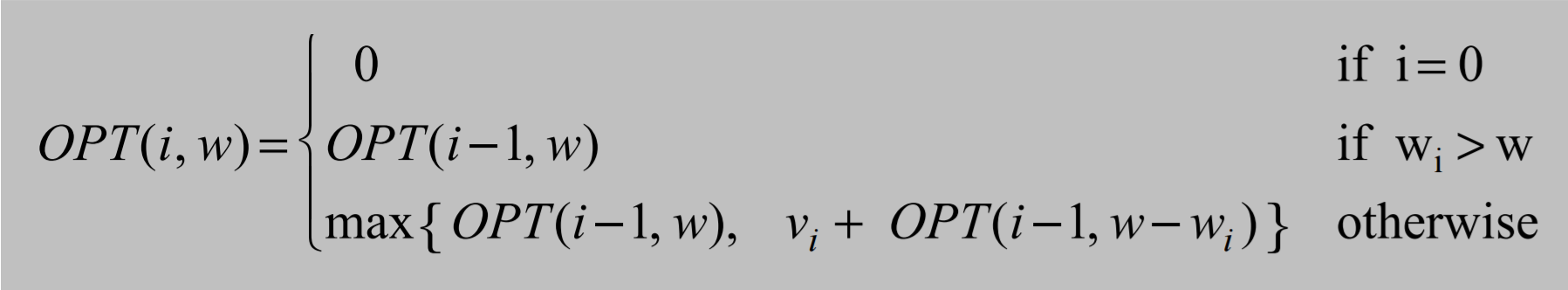/knapsack-problem

Implementation of the 0-1 Knapsack Problem

Primary LanguageJava

0-1 Knapsack Problem

Implementation of the 0-1 (binary) Knapsack Problem
Technically an NP-Hard problem, so this solution doesn't scale for large values of the Knapsack Capacity

Optimal Substructure

w is the current max weight of the knapsack (goes from 0 to W, the actual max weight of the knapsack)

  • If wi>W, the item it too heavy to fit in the knapsack, so we copy the value from row above: OPT(i-1,w)
  • If the item CAN fit there are 2 cases
    1. The current item is not included, just copy from row above: OPT(i-1,w)
    2. Current item IS included, add it's value & find OPT for a new weight: vi + OPT(i-1,w-wi)

Pseudocode

Finding the Knapsack's Contents

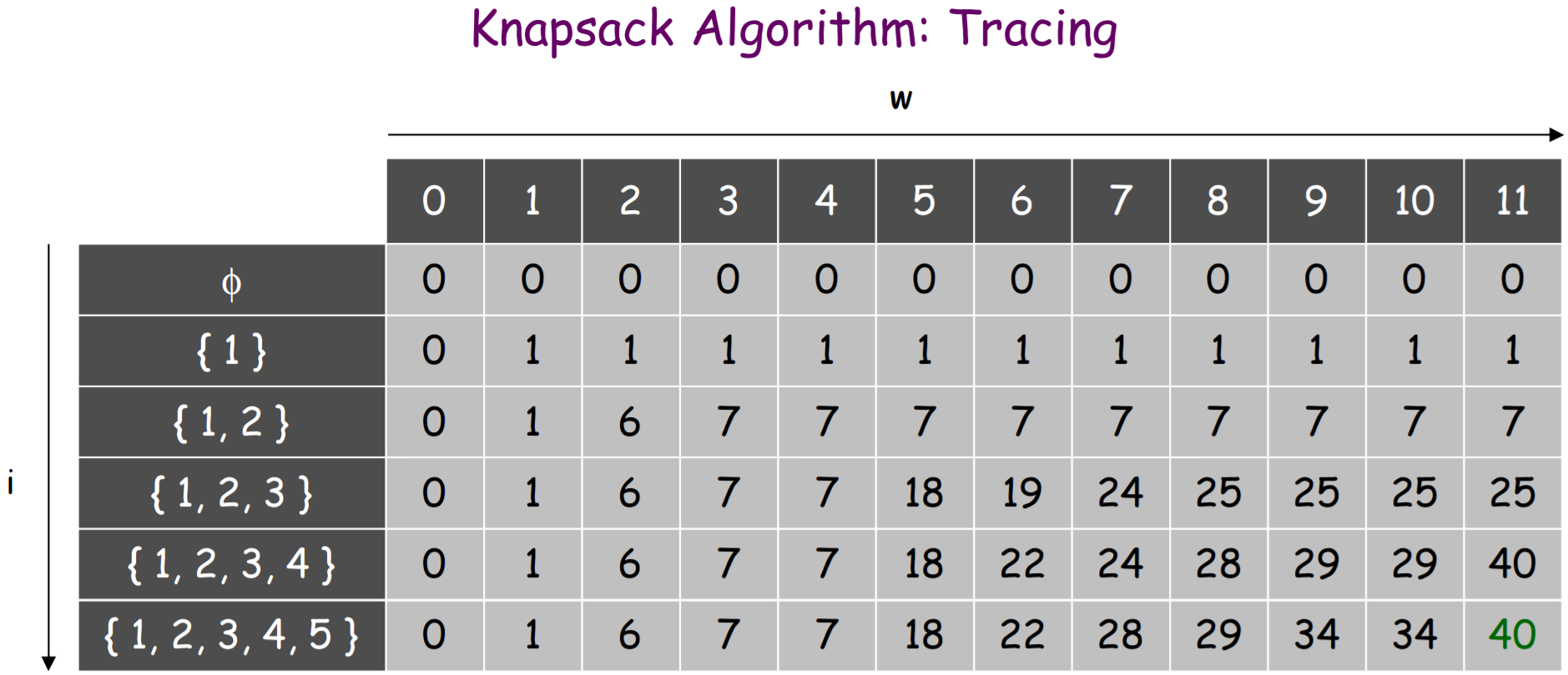
A slightly different version of the algorithm, but the point is the final loop that recovers the items from the keep array

Example Problem

This program runs on 5 items with 2 different weight capacities: 11 and 10

Capacity=11 Solution

Optimal Solution is total value=40 from item 3 & 4

Notes

  • solveKnapsack() populates the memoization table & finds the maximum weight possible
    • memoizationTable is filled with -1 to distinguish from completed rows
    • Then 0th row is filled with 0
    • memoizationTable is printed using printTable() after each row is completed
  • findOptimalKnapsackContents() is called after solveKnapsack() to see what items were actually added
  • The ID or name of an Item is its array index
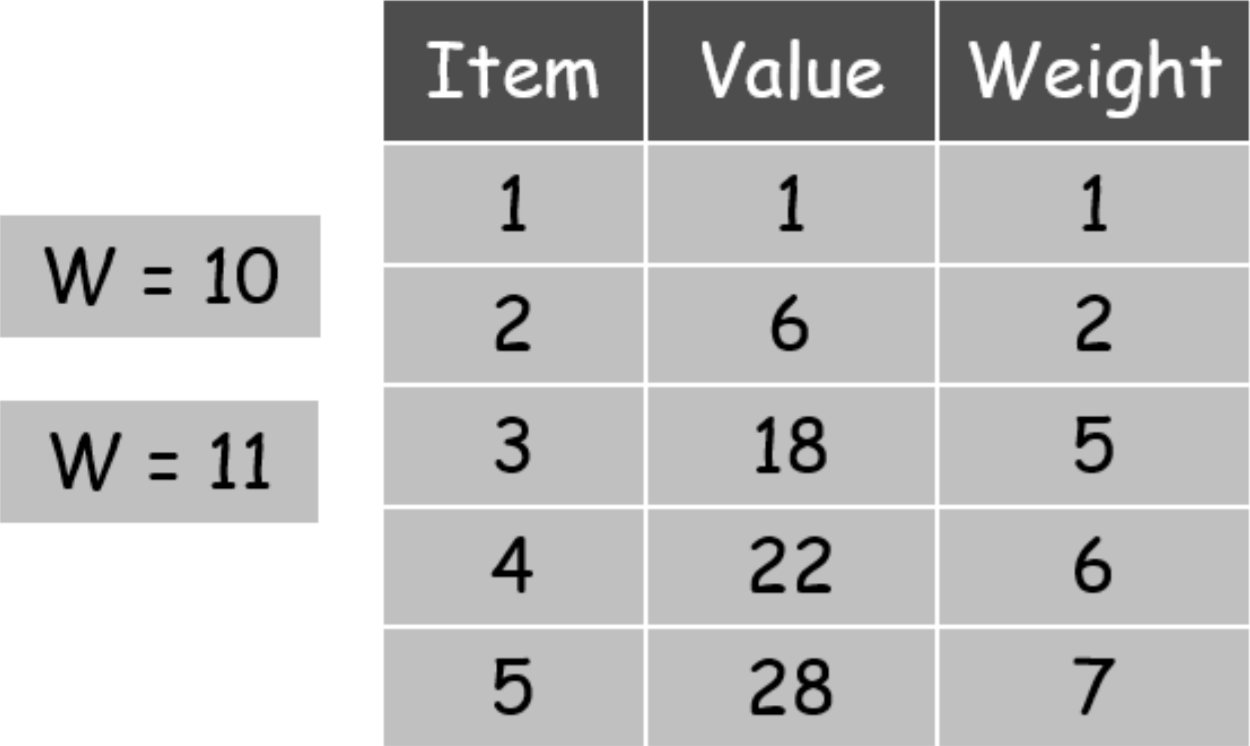
  • Must be non-negative integer weights
  • Run with different items by changing arrays for values, weights & numberOfItems
    There is no error checking between those 3 fields, so hard-code them into the constructor
    verifyCorrectArrayLength() can be used to see if the array lengths match numberOfItems, but it's not enforced
  • View output with fixed-width font for columns to line up (configure your IDE or copy to new document)

Code Details

  • Arrays are indexed from 1 to make human readable
  • Put a 0 as the 1st element of values and weights
  • memoizationTable and chosenItems are both initialized to dimensions [numberOfItems+1][knapsackWeightCapacity+1] to keep it indexed from 1
  • Pseudocode has a step to set all values in 0th row to 0. Not needed since Java initialized the entire 2D array to 0's
  • findWidestNumberInTable(), findWidestElementInList() and leftPad() are all helper methods used by printTable()
  • printTable() is pretty fancy & prints padding spaces to the left of numbers so the columns line up. It looks nicer, but doesn't have to be that complicated
  • solveKnapsack() populates memoization table & adds true to the corresponding cell in chosenItems matrix when an item is added
  • findOptimalKnapsackContents() works backwards from the bottom right corner of the chosenItems matrix
    • A true in chosenItems means that an item was added to get that max value when calculating memoizationTable, false means it just copied the value from the row above
    • Start with currentCapacity=knapsackWeightCapacity
    • i goes from numberOfItems down to 1
    • If a value is true, we included that item in the knapsack so output the item @ row i
    • Since we included an Item, subtract its weight from currentCapacity ( currentCapacity -= weights[i] -= weights[i] )
      This will move the currentCapacity left some number of columns
    • Continue until it reaches the 1st row
    • Done