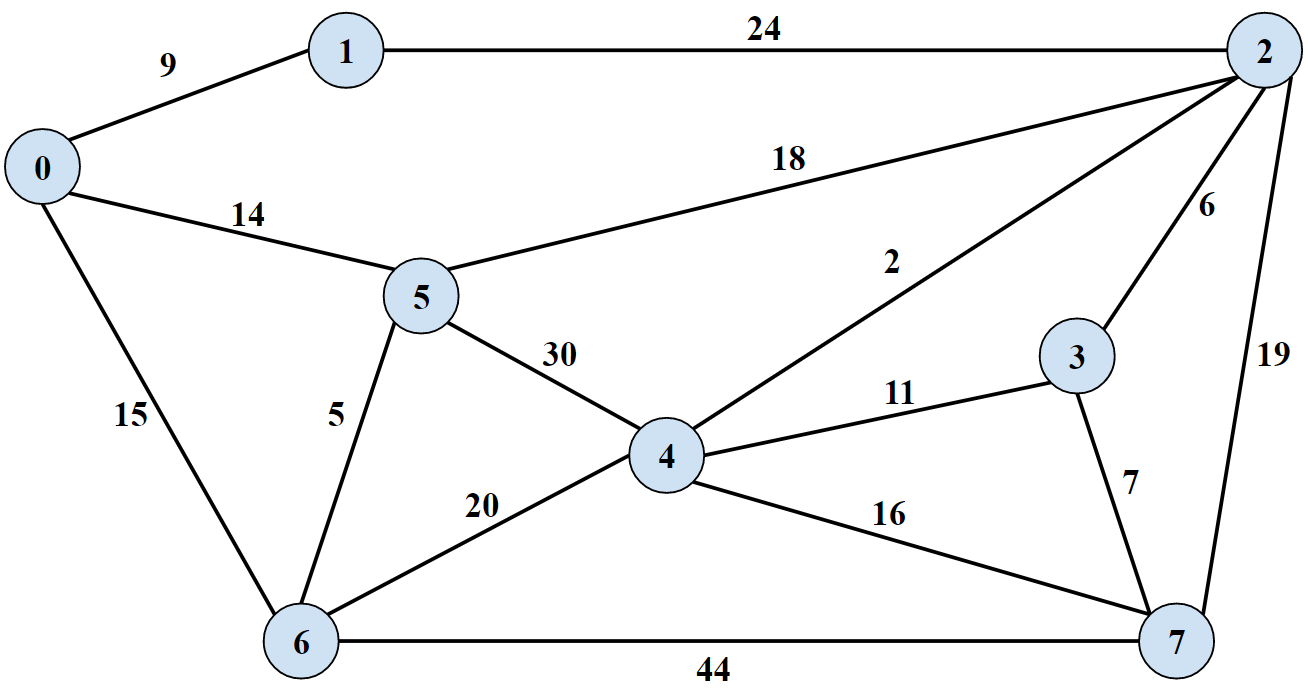
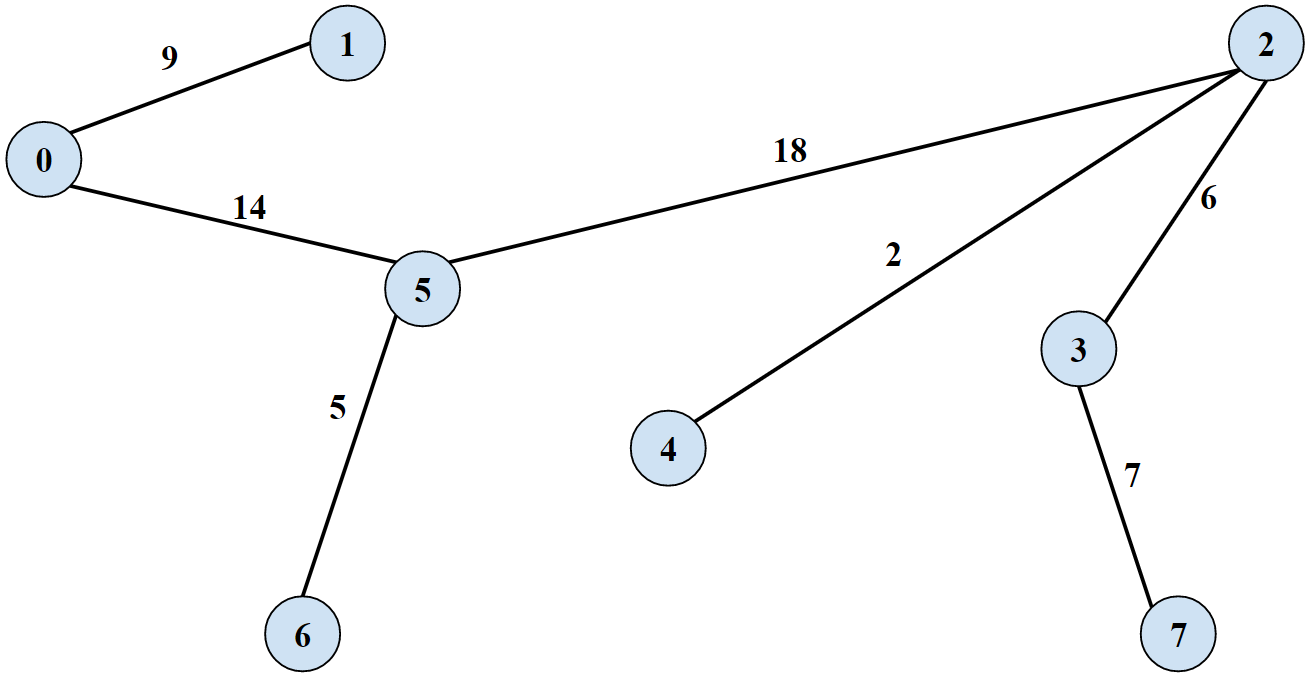
Greedy Algorithm to find a minimum spanning tree in an undirected graph by deleting heaviest edges unless it would disconnect the graph
Minim Spanning Tree: a subset of nodes that touches all vertices while keeping all nodes connected and uses the sum of the edge weights in a minimum
A Minimum spanning tree yields a graph with M-1 edges because adding 1 more edge would by definition create a cycle
Start with all edges in the tree T. Consider edges in descending order of weight. Delete edge from T unless doing so would disconnect T
- Sort edges by weight
- Initialize MST with all edges
- Delete the highest weight edge
- If deleting the edge disconnects the graph, add it back
- Otherwise continue
- Node names are consecutive integers starting from
0 - Create a graph:
ArrayList<Edge> graph = new ArrayList<Edge>(); - Graph undirected edge list, but only add each edge once
- In the graph there is an edge from
0to9with weight=9 - This bidirectional edge can just be represented once:
graph.add(new Edge(0, 1, 9));
- In the graph there is an edge from
- Count the vertices in the graph:
int vertexCount = 8; - Call the static method
ReverseDeleteMST.findMST(graph, vertexCount);
- Due to the implementation of Breadth First Search, the code creates an additional copy of the graph as an adjacency list
- This adjacency list graph is the one where edges are deleted, the original input graph as an edge list is left in tact
- The MST is technically built up from nothing and added to if deleting an edge in the adjacency list would disconnect the graph
- Kevin Wayne Slides
- University of Illinois - Minimum Spanning Trees
- T. M. Murali Slides
- Fan Chung Graham Slides
- Reverse Delete Algorithm - GeeksForGeeks Algorithm strategy, code only briefly referenced
- Remove items from ArrayList with certain value - Stack Overflow Lambda expression to delete specific value from
ArrayList