/CAPM_Test_Share

marp theme _class backgroundImage
true
gaia
lead
url()

The Conditional Captital Asset Pricing Model Revisited: Evidence from High-Frequency Betas

MANAGEMENT SCIENCE 2020 Fabian Hollstein et. al.

苏锦华 2022.04

Content

  • Introduction
  • Data and Methodology
    • Historical Beta, Realized Beta, Hybric Beta
  • The Conditional CAPM Revisited
    • Size, Value, Monmentum
    • Alternative Windows Lengths, Frequencies, Conditioning
  • The Precision of High-Frequency Betas
    • RMSE, Regression
  • Conclusion

Introduction

本文重新研究了条件CAPM的在高频数据下的表现。在一个2500多只股票的大样本，包括1996年至2014年期间的每日和高频数据，以实证检验条件资本资产定价模型是否能够解释资产价格异常。

Conditional CAPM能否解释超额收益

conditional CAPM(day): small, big, growth, value, loser, and winner

value (value minus growth) momentum (winners minus losers) size (small minus big)

conditional CAPM(30m): small, big, growth, value, loser, and winner

Data and Methodology

Data

  • 时间：1996年1月至2014年12月的样本期美国股票
  • 来源:
    • 证券价格研究中心（CRSP）的每日和每月价格和回报以及股息支付和流通股数据
    • Tick History（TRTH）数据库收集高频价格数据
  • 范围:
    • 在纽约证券交易所（NYSE）、美国证券交易所（AMEX）和美国证券交易商协会自动报价系统（NASDAQ）上交易的所有股票
  • 其他辅助数据
    • 利率期限结构的数据--IvyDB
    • 无风险（一个月期国库券）利率--Kenneth French
  • 数据处理
    • 排除了非常缺乏流动性的股票
    • 交易时间过滤
    • 利用CRSP提供的股票分割和分配数据来补充TRTH数据，以调整TRTH隔夜收益率
    • 为了防止小型股票非交易的潜在影响（Gorodnichenko和Weber 2016）主要研究30分钟的频率

Data and Methodology

Historical Beta

$$ \beta_{j, t}^{\mathrm{HIST}}=\frac{\operatorname{cov}\left(r_{j}-r_{f}, r_{M}-r_{f}\right)}{\operatorname{Var}\left(r_{M}-r_{f}\right)} $$

$$ \begin{aligned} r_{j, \tau}-r_{f, \tau}=& \alpha_{j, t}+\beta_{j, t}^{(0)}\left(r_{M, \tau}-r_{f, \tau}\right)+\beta_{j, t}^{(1)}\left(r_{M, \tau-1}-r_{f, \tau-1}\right) \\ &+\beta_{j, t}^{(2)}\left(\sum_{n=2}^{l} r_{M, \tau-n}-r_{f, \tau-n}\right)+\epsilon_{j, \tau} \end{aligned} $$

Data and Methodology

Realized Beta

$$ \beta_{j, t}^{\mathrm{HF}}=\frac{\sum_{\tau=1}^{N} r_{j, \tau} r_{M, \tau}}{\sum_{\tau=1}^{N} r_{M, \tau}^{2}} $$

Hybird Beta

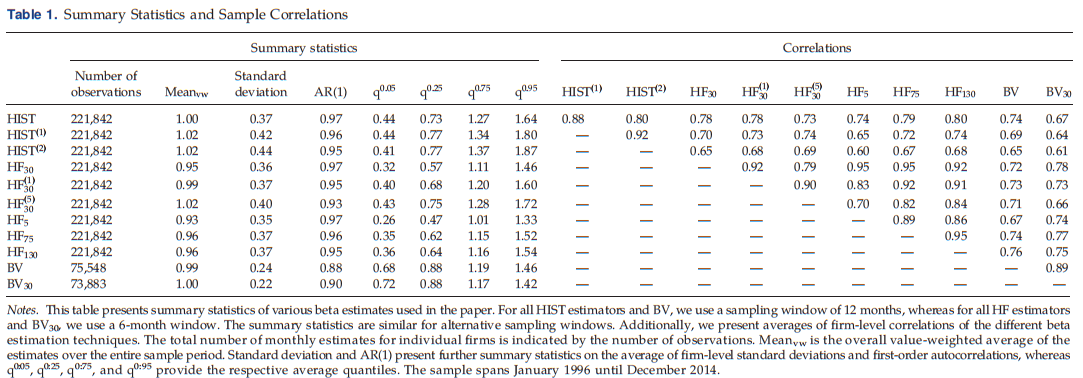
$$ \beta_{j, t}^{\mathrm{BV}}=\frac{\sigma_{j, t, T}^{\mathbb{Q}} \sum_{i=1}^{N} \omega_{i, t} \sigma_{i, t, T}^{\mathbb{Q}} \rho_{j i, t}^{\mathbb{Q}}}{\left(\sigma_{M, t, T}^{\mathbb{Q}}\right)^{2}} $$

Data and Methodology

Summary Statistics and Correlation Analysis

  • 所有历史和高频估计器的总观测数都要高得多，主要是因为混合估计器只能在每个时间点对标准普尔500指数
  • 添加滞后Beta会显著增加HIST中的测量误差,估计器中的噪声自然会增加标准偏差，并在AR（1）系数中产生衰减偏差
  • 由于HIST的加权平均值为1.00，几乎没有证据表明HIST存在系统性偏差,因此，我们主要讨论无滞后调整的估计量
  • 相比之下，高频估计器的加权平均β值略低于1，对于某些股票而言，不频繁且不同步的交易可能会使贝塔系数偏向于零。加上一个滞后，加权平均值上升
  • 观察到历史每日和30分钟高频估计器之间的相关性为0.78

The Conditional CAPM Revisited

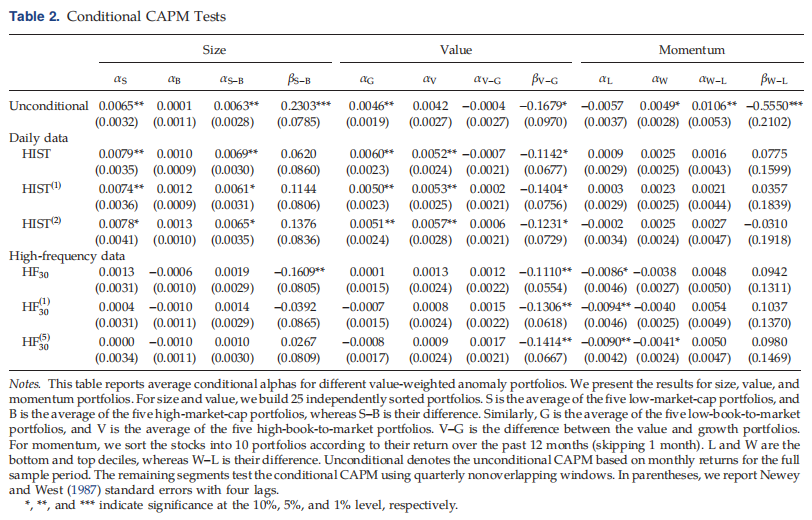
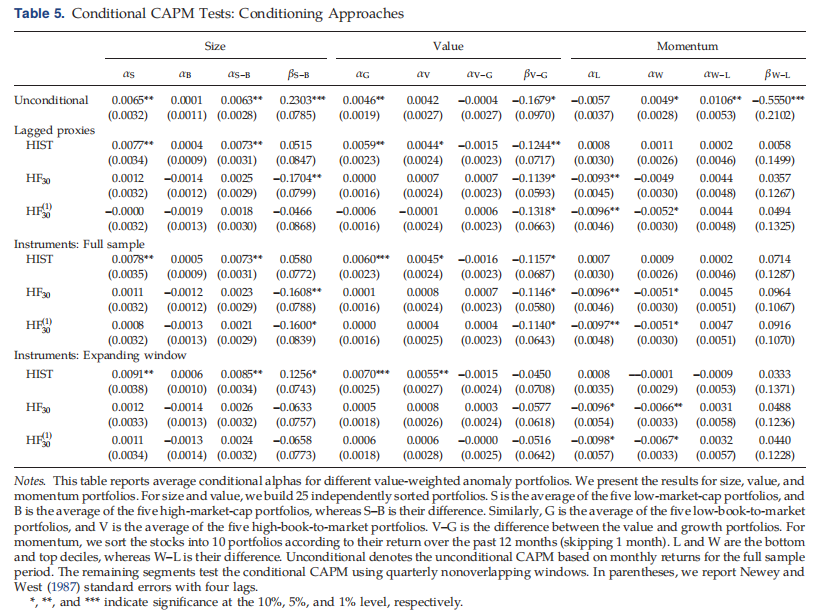
Setup 实证试图研究以下问题：高频贝塔估计值下条件CAPM表现如何？高频贝塔能帮助解释为什么小公司的股市收益通常优于大公司吗？如何解释高频Beta相对于低频Beta的优势？条件CAPM模型能否解释为什么过去的赢家股票通常表现优于过去的输家股票？ 本文遵循Lewellen和Nagel（2006）提出的方法，直接估计条件β，同时获得条件α的估计。借此对整个样本进行划分(季度非重叠窗口)，容许条件β时序变化，用于无条件测试。对于每个异常投资组合的条件α和β。得到条件α的时间序列，我们可以通过测试平均α是否显著不同于零来直接测试条件CAPM。使用稳健的Newey和West（1987）标准误差和四个滞后来评估统计显著性。

对于所有异常投资组合，利用纽约证券交易所断点，对相应股票条件α和β进行加权平均得到投资组合的条件α和β。我们按照Lewellen和Nagel（2006）的观点构建了Size和Value投资组合。构造的出发点主要是账面市盈率相关数据，每个月将这些股票独立分类为25个大小的账面市值投资组合，并根据这些投资组合的组合进行测试：

  • S(small)是五个低市值投资组合的平均值
  • B(big)是五个高市值投资组合的平均值，而S–B是它们的差异
  • G(groth)是五个低账面市值投资组合的平均值
  • V(value)是五个高账面市值投资组合的平均值，V–G是价值和增长投资组合之间的差异
  • momentum是根据之前12个月的回报率将股票分为10个投资组合，而跳过最近1个月（Jegadeesh和Titman 1993）
  • L（loser）和W（winner）是底部和顶部的10%位，W–L是赢家和输家投资组合之间的差异

The Conditional CAPM Revisited

Unconditional & Conditional CAPM

The Conditional CAPM Revisited

Underconditioning Bias

$\alpha_{j}^{\text {unc }}-\bar{\alpha}{j}^{\text {cond }}=\left(1+\frac{\bar{R}{M}^{2}}{\sigma_{M}^{2}}\right) \operatorname{cov}\left(\beta_{j, t}, \mathbb{E}{t}\left(R{M, t}\right)\right)$ $\frac{-\left(\frac{\bar{R}{M}}{\sigma{M}^{2}}\right) \operatorname{cov}\left(\beta_{j, t}, \mathbb{E}{t}\left(R{M, t}^{2}\right)\right)}{\text { market-timing bias }}$ $\underbrace{-\left(\frac{\bar{R}{M}}{\sigma{M}^{2}}\right) \operatorname{cov}\left(\beta_{j, t}, \sigma_{M, t}^{2}\right)}_{\text {volatility-timing bias }}$,

继Lewellen和Nagel（2006年）和Boguth等人（2011年）之后，我们现在研究了欠条件(underconditioning)可能引入的潜在偏差（即当β确实随时间变化时，使用无条件CAPM而不是传统CAPM）。Boguth等人（2011年）表明，如果条件α与市场超额收益不相关，则无条件α中的偏差等于无条件α与平均条件α之间的差异。 欠条件偏差包括市场时间偏差和波动时间偏差。市场时机偏差源于条件β与预期市场超额收益或预期市场超额收益平方的协变量，反映了β可能随商业周期而变化的事实（Jagannathan和Wang，1996），“通常小于0.20%”的偏差，“最大为0.35%”。波动时间偏差源于条件β与市场条件波动的负协变量，这似乎对动量尤其明显，波动时间偏差达到每月0.10%到1.01%之间的值。对于本文样本中的投资组合，Alpha的绝对值在大盘对开本的每月0.01%和momentum反常投资组合的每月1.06%之间。

  • 因此，我们观察到的无条件回报的幅度可能与欠条件的偏差一致。

The Conditional CAPM Revisited

Alternative Windows Lengths, Frequencies, Conditioning

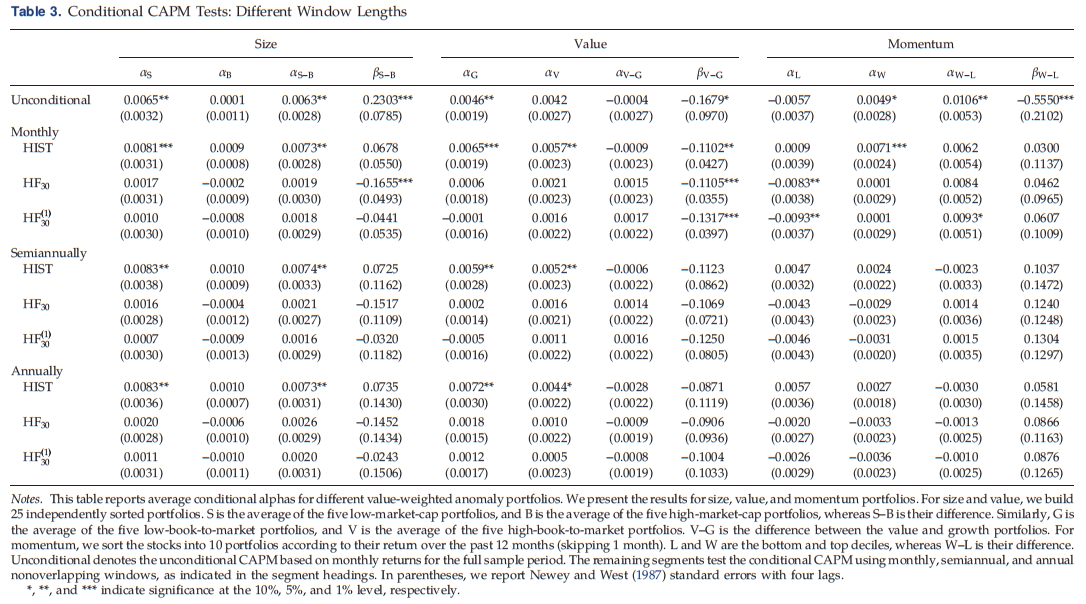
使用三个月的窗口来估计条件α和β。然而，窗口长度涉及到一个权衡：一方面，较短的窗口可能会提高模型的性能，因为它允许在beta中有更大的变化；另一方面，更长的窗口可以提高条件alpha和beta估计的精度，并以这种方式改善模型性能。因此，在表3中检查了1个月、6个月和12个月的替代窗口长度。只报告主要估计器HIST、HF30和HF（1）30的结果。如表所示，这些变化并不影响主要结论。

The Conditional CAPM Revisited

Alternative Windows Lengths, Frequencies, Conditioning

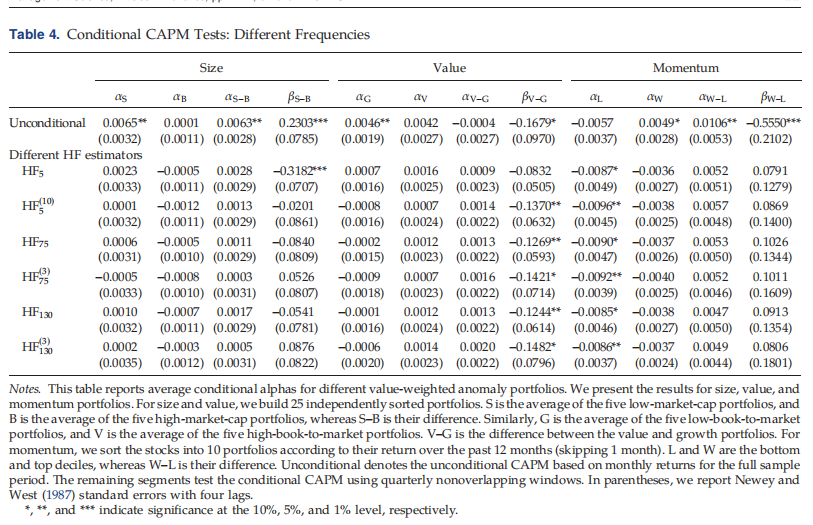
检查高频估计模型的替代采样频率对结果的影响。根据有无滞后的5分钟、75分钟和130分钟数据检验了参数估计。对于所有这些估计模型，我们获得了与HF30定性相似的结果：基于高频数据的条件CAPM可以解释Size、Value和Momentum异常。

The Conditional CAPM Revisited

Alternative Windows Lengths, Frequencies, Conditioning

Boguth等人（2011年）警告说，可能会在分析中引入偏差，因为用于计算条件α的贝塔估计值在投资者进行投资之前是无法事先获得的。为了检查我们的结果是否受到这种偏见的影响，我们使用三种不同的替代方法重复前面的分析。首先，我们只是使用滞后的beta作为未来beta的代理。其次，我们估计下述回归方程。

$$ \beta_{j, t}=a_{j}+b_{j} \beta_{j, t-1}+\epsilon_{j, t} $$

本文使用了这种方法的两种变体：一种是使用Boguth等人（2011）中的完整样本，另一种实时实现的，只使用时间t之前的数据，并使用36个月窗口初始化的扩展窗口。我们在表5中给出了这些方法的结果。结果与baseline非常相似。我们发现，基于高频数据的条件CAPM仍然可以解释所有三种情况下的大小、值和动量异常。

The Precision of High-Frequency Betas

$$ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum_{t=1}^{n}\left(\beta_{t, T}^{\mathrm{R}}-\beta_{t}\right)^{2}}, $$

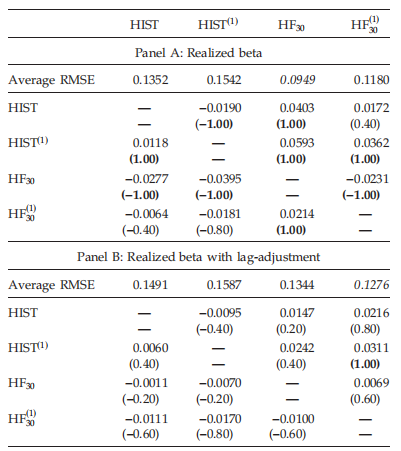
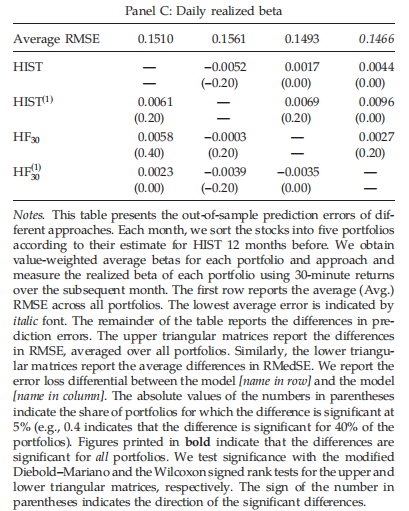
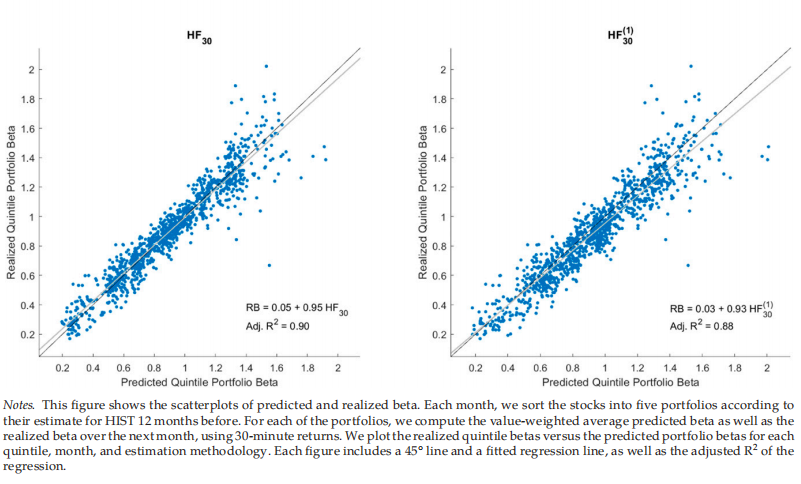
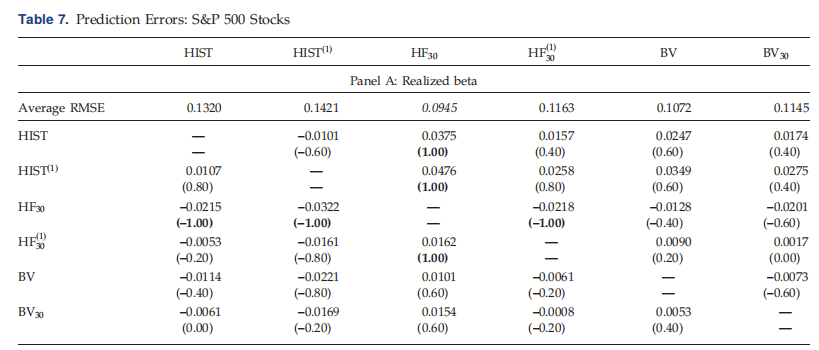
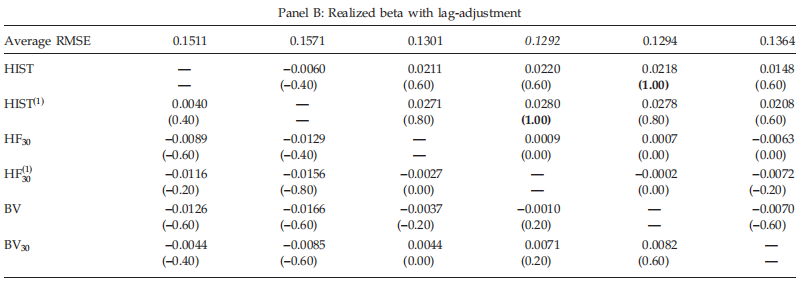
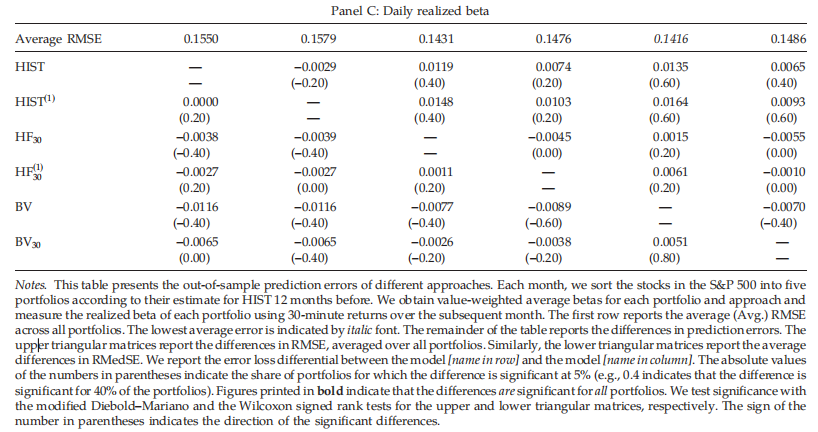
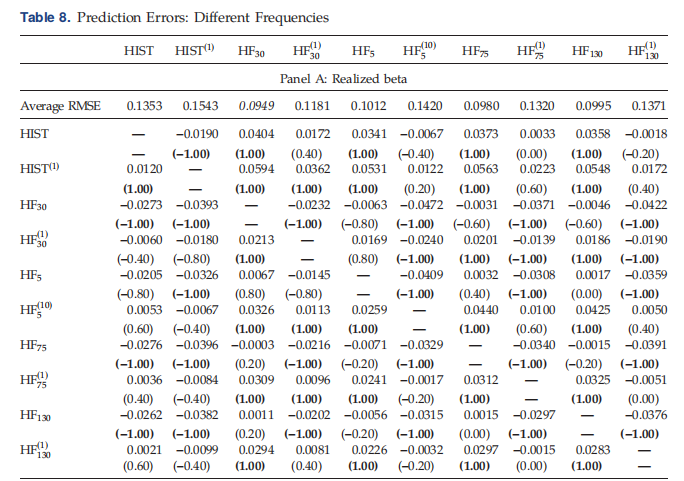
计算不同方法的样本外预测误差。每个月，我们都会根据过去12个月的估值，将这些股票分为五个投资组合。我们获得每个投资组合和方法的价值加权平均贝塔值，并使用随后一个月的30分钟回报率衡量每个投资组合的已实现贝塔值。第一行报告所有投资组合的平均RMSE。括号中数字的绝对值表示差异显著的投资组合份额为5%（例如，0.4表示差异显著的投资组合份额为40%）。用改进的Diebold–Mariano和Wilcoxon符号秩检验对上下三角矩阵进行显著性检验。括号中数字的符号表示显著差异的方向。

The Precision of High-Frequency Betas

h:500h:500

The Precision of High-Frequency Betas

The Precision of High-Frequency Betas

The Precision of High-Frequency Betas

The Precision of High-Frequency Betas

The Precision of High-Frequency Betas

The Precision of High-Frequency Betas

The Precision of High-Frequency Betas

$$ \beta_{t, T}^{\mathrm{R}}=a+b \beta_{t}+\epsilon_{T}, $$

The Precision of High-Frequency Betas

$$ \beta_{j, t, T}^{\mathrm{R}}=a_{T}+b_{T} \beta_{j, t}+\epsilon_{j, t, T}, $$

Conclusion

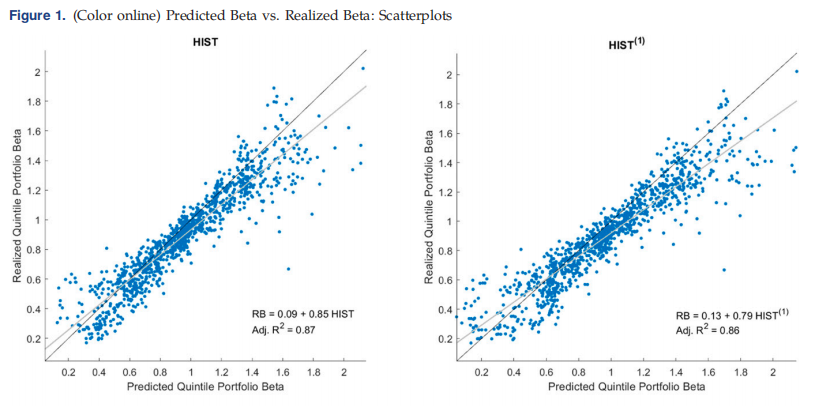
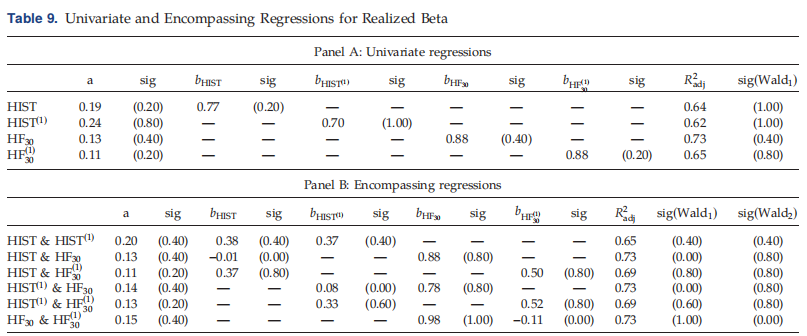
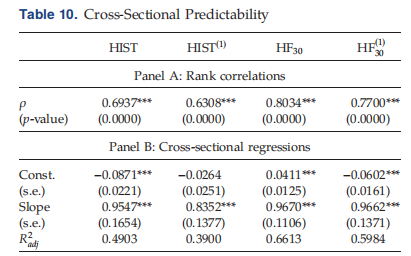
本文基于日数据和高频数据，用betas检验了条件CAPM。而对于日常数据，该模型无法解释规模异常和三个主要异常的六个组成部分中的三个，而条件CAPM可以解释规模、价值和动量异常，以及使用高频数据时六个组成部分投资组合中的五个。我们发现，高频贝塔的优越经济价值与未来实现贝塔的优越可预测性有关。从高频数据估计的贝塔值比从日收益数据估计的贝塔值要准确得多。我们发现，在Mincer–Zarnowitz回归中，从高频数据估计的Beta也优于基于每日数据的Beta，并且具有更好的横截面可预测性。