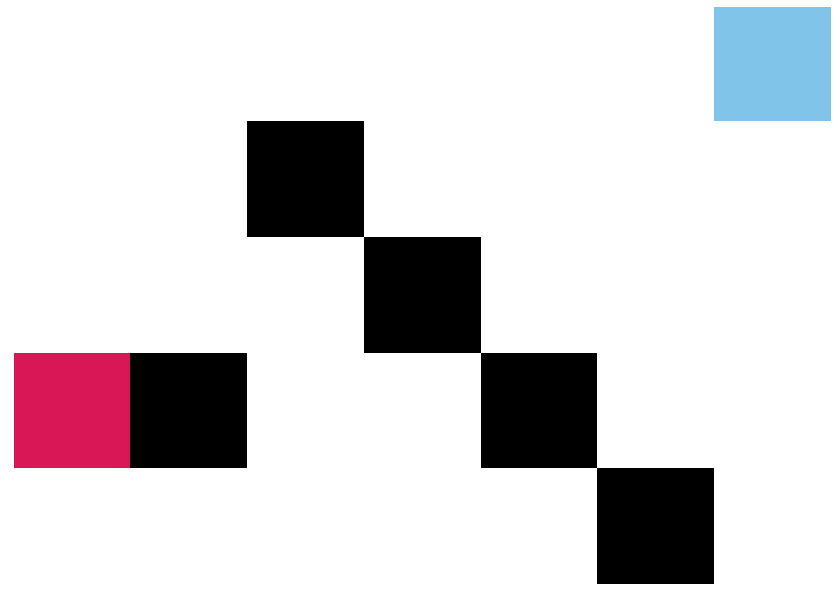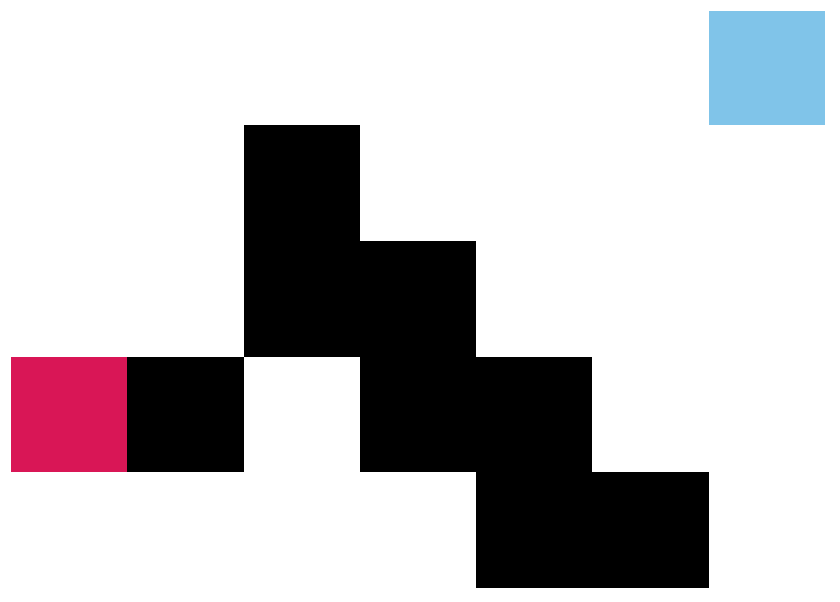算法课程作业。
主要是探寻 A* 路径规划算法,咱附带实现了一下 JPS 版本的 A* 算法,支持对角障碍物的阻塞和绕路处理。
还别说,路径规划真挺有趣吧~ (。・∀・)ノ
A* 算法:
a_star.mp4
带对角障碍物绕路机制的 Jump Point Search 算法:
a_star_jps_detour_fixed.mp4
src
├── algorithms # 算法实现
│ ├── __init__.py
│ ├── a_star.py # A* 算法
│ ├── a_star_jps.py # A* 算法 Jump Point Search 版
│ ├── a_star_jps_detour.py # A* 算法 Jump Point Search 版,支持对角障碍绕路
│ ├── a_star_jps_detour_fixed.py # (本仓库中最好的一版算法实现)A* 算法 Jump Point Search 版,支持对角障碍绕路,修正了绕路后的搜索策略,能解得和 A* 一样的路径代价。
│ ├── a_star_jps_detour_failed.py # 失败的绕路实现
│ ├── algorithm_base.py # 算法基类
│ ├── states.py # 算法状态枚举量
│ └── utils.py # 工具类,主要是方向 Direction 相关的类
├── exceptions
│ └── __init__.py # 一些自定义异常
├── problems
│ ├── __init__.py
│ ├── cell_status.py # 图中每个格子状态的枚举量
│ ├── drawer.py # 问题绘制模块
│ ├── generator.py # 随机问题生成
│ ├── problem.py # 问题类,用于表示每个二维栅格图
│ └── utils.py # 工具方法
├── test.py # 一些测试用例
├── requirements.txt # Python 依赖
├── problem.bin # 一个示例问题,可以用 Problem.from_file 载入(pickle v4,要求 Python >= 3.4)
└── visualization
├── __init__.py
├── algo_animator.py # 算法执行过程动画化模块
├── problem_visualizer.py # 将问题进行可视化的模块
├── result_visualizer.py # 将求解结果进行可视化的模块
└── utils.py # 可视化相关的工具方法各个方法的调用方式可以参考 test.py 以及各个方法的 docstring 注释。
每个算法实现的 .py 文件头部都有一些说明。
a_star.py- 传统 A* 算法实现。a_star_jps.py- 传统 JPS 算法实现,diagonal_obstacles=True时穿不过 这种对角障碍,但是可以通过
这种对角障碍,但是可以通过  这种角障碍。
这种角障碍。a_star_jps_detour.py- 支持绕过角障碍物的 JPS 算法实现,对于这种情况会绕路: 。
。a_star_jps_detour_fixed.py- 在a_star_jps_detour的基础上添加了绕路后的额外搜索策略,让求解得到的路径代价和 A* 的一致。
Dijkstra 算法每次迭代中都会从目前未确定结点中选择路径最短的结点作为下一个落脚点,然后再扩展其所有的可行邻居结点。虽然 Dijkstra 能保证找到最短路,但是因为其扩展的速度特别慢,会均匀地探索各个路径,对于规模很大的图,求解速度实在是令人不敢恭维。
- 注意,Dijkstra 要求边权非负。
A* 算法则是在 Dijkstra 的基础上,加入了启发式信息(这个信息就是“是否沿着这个方向更有可能快速到达终点”),使得其能够优先扩展更有希望的结点,从而加速搜索过程。
- A* 算法的性能因此也取决于启发式信息的计算方式(不一定能找到最优路线),在障碍物比较复杂时可能性能上会退化到 Dijkstra。
Jump Point Search 优化的 A* 算法则要厉害多了,其通过一些策略大幅减少了需要扩展的结点数量,每次扩展的结点是一个“跳点”。
💡 从上面也可以看出来,路径规划算法在性能方面一个很重要的点就是——扩展结点的策略。
- 扩展结点换个说法,其实就是程序认为可能存在于最优路径上的结点。程序会从这些结点出发寻找下一个可能的落脚点。
- 因此迭代过程中需要扩展的结点越少,需要检查的结点就越少,算法的内存消耗就越小,同时相对来说也能更快求解(但不一定更快,取决于实际情况)。
JPS 优化的 A* 算法中最重要的两个概念:
- 强迫邻居
- 跳点
具体概念的介绍不多赘述,可以见参考文章。
个人认为,要清晰地写代码实现 JPS-A* 算法,必须要搞清楚 JPS 的核心优化点在哪里——
——没错,就是对扩展结点策略的优化!
A* 算法每一次迭代在取出一个落脚点后,都会扩展其所有邻居结点;JPS 额外多了一些计算步骤,找到所谓的“跳点”,扩展的是跳点而不是邻居,而每次迭代中找到的跳点的数量要明显少很多,因此求解速度明显就要高很多。
💡 简单来说,JPS 相比 A* 算法,改动的地方其实就是扩展结点的部分(比如在 A* 中就是寻找邻居并加入 open_list 这部分)。
算法实现过程中最让我迷惑的一点:强制邻居(Forced Neighbor)到底是什么个地位?! 到底要不要把强制邻居加入 open_list ?很多文章都没讲清楚或没强调这一点。
折腾了好一段时间,总算把 JPS 算法实现后,我的答案是:
- 不需要加入
open_list!
强制邻居的作用主要有两个:
- 用于判定跳点。(跳点周围肯定有强制邻居)
- 用于引导扩展结点。
第 1 点很多文章都写的很明确,就不多赘述了。主要是第 2 点。
关于 JPS 算法的基础知识这里咱就不多赘述了...(⊙x⊙;)
我觉得整个过程中最让我迷糊的可能就是这个地方了。
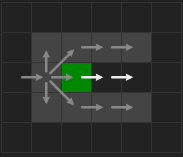
在从 open_list 取出一个结点后,在 A* 算法中有 8 个邻居,这其实也可以看作是 8 个寻找方向,但在 JPS 算法中,大部分情况下我们并不需要向所有 8 个方向进行搜索。
- 设结点
$x$ 的父(前驱)结点是$parent(x)$ ,所谓的“方向”就是$parent(x)$ 指向$x$ 的这个方向。
图中标出来了 8 个“邻居”的位置,在 JPS 中这是 8 个寻找方向。
- 上图中是一个起始节点,其没有父结点,因此需要向 8 个方向去查找跳点,将跳点加入
open_list。
也就是从 open_list 取出的第二个结点开始,就全都是跳点了。
当然,把起始结点看作跳点也行。
每个跳点都有路径上的父(前驱)结点,有父结点的结点就有方向。而有方向,JPS 就能顺着方向找跳点,有两种情况:
-
水平/竖直方向。
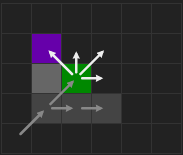
沿着这个方向一直走直到遇到特定的(见参考文章)障碍物,就有了强制邻居(紫色),也就找到了跳点。
-
对角方向。
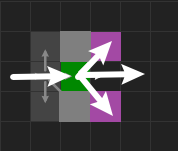
先沿着水平和竖直分量方向按 1 进行,然后再沿着对角线方向走一步。反复这个过程直至遇到特定的(见参考文章)障碍物,就有了强制邻居(紫色),就找到了跳点。
特例:终点没有强制邻居。
注意,这里强制邻居的作用就来了!
上面每个右图中绿色的结点肯定是从 open_list 中取出的跳点,因为其有强制邻居(紫色方块),设其为点
-
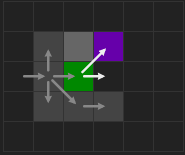
对于 1 中的情况,原本从
$A$ 出发找跳点的方向是一直向右,出现强制邻居后,新增了一个指向强制邻居的寻找方向。 -
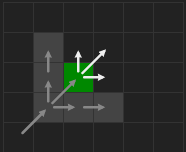
对于 2 中的情况,原本从
$A$ 出发找跳点的方向是两个分量和一个对角方向,出现强制邻居后,新增了一个强制邻居的寻找方向。
💡 因此每次取出跳点
-
计算这个跳点
$A$ 的方向($parent(A) \rightarrow A$ 的这个方向)。 -
如果是水平/竖直方向,则从
$A$ 出发有一个寻找方向;如果是对角方向,则从$A$ 出发有三个寻找方向(见参考文章)。 -
扫描一圈检查
$A$ 有几个强制邻居,每找到一个强制邻居,就加上一个寻找方向。 -
沿着这些方向去寻找跳点,将新找到的跳点加入
open_list,再进入下一次迭代。
所以说强制邻居的有引导跳点查找的功能,而 JPS 扩展的是跳点,因此强制邻居其实就是在引导结点的扩展。
创建算法对象的时候有一个参数 diagonal_obstacles 可供配置,默认为 True,其决定算法在执行搜索时是否能穿过对角障碍物,类似下面这些情况:
✨ 咱之所以想到添加这个参数,是因为在实际应用中为机器人规划路线时,这样斜着穿过对角障碍物的情况会导致机器人与障碍物发生碰撞。
- 若
diagonal_obstacles=True,程序会把这种障碍物考虑在内,搜索时不会穿过这样的障碍物。 - 若
diagonal_obstacles=False,程序会忽略这种障碍物,搜索时就可以直接穿过。
❗ 但问题随之而来,JPS 算法是很依赖于对角方向的移动的。上面 Case.1 虽然影响不大,但是 Case.2 可能会使得 JPS 无法求解,比如:
这种情况下很明显 JPS 只能搜索左侧这一部分,而右侧的搜索方向因为有 Case.2 的对角障碍物,完全被封死了,导致算法无法求解。
对于 Case.2 的对角障碍物,我希望 JPS 算法能多走几步以绕过障碍物,像这样:
实现的时候我并没有改变 JPS 的搜索策略,JPS 算法仍然继续沿着红色箭头这个方向搜索跳点,实际上我只是暂时记录了红色框代表的绕路结点(_add_bypass_pos)并修正了到达右上角的路径长度(L301, L381)罢了。
- 注意,路径长度必须立即修正,不然可能影响到算法的搜索过程。
🤔 会遇到绕路情况的操作有两种:
- 从
open_list取出一个结点后确定搜索方向时(_find_directions)。 - 沿着搜索方向查找跳点时(
_jump)。
在算法求解完成后,生成路径的时候,再把所有在录的绕路结点都加进去(solved_path_coordinates)。
💡 这部分的实现位于 a_star_jps_detour.py 中。
📝 PS:观察到很有意思的一点,如果考虑绕过这些障碍物,JPS 解出的路径代价和 A* 可能是不同的,可能是次优解;但是如果不考虑对角障碍物,JPS 和 A* 解出的代价几乎总是相同的。
- 这大概是因为 JPS 在设计之初就假设是可以斜着穿过这种对角障碍物(Case.2)的,而我设计的绕路方式没有修改算法的搜索机制,导致算法没有考虑到添加绕路结点后可能存在的更优的关键点。
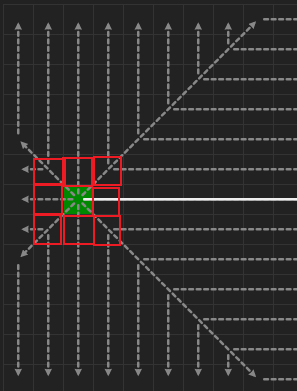
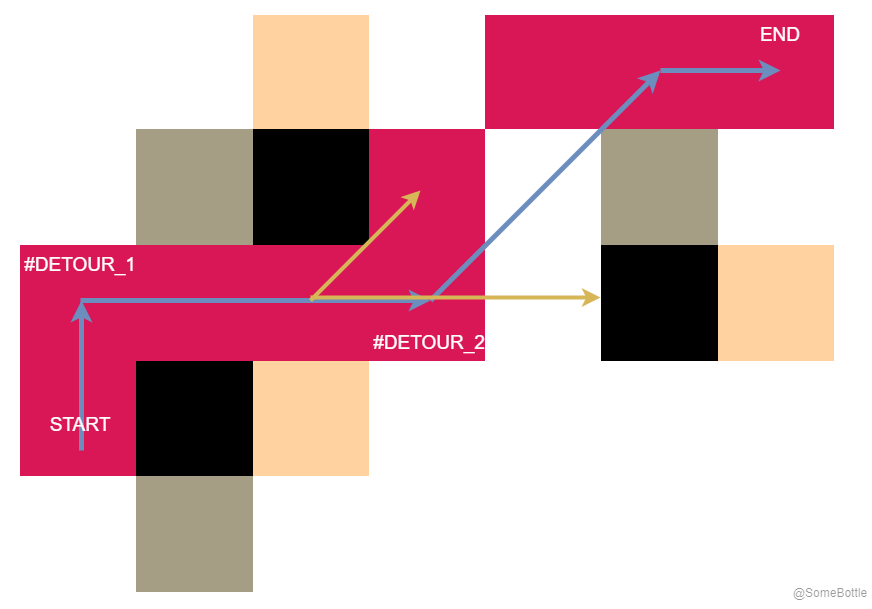
上面提到,像我这样的绕路机制,JPS 可能找不到和 A* 一样的优解。
红色块为a_star_jps_detour求解得到的路线;黄色块为open_list中的结点;绿色块为closed_list中的结点;黑色块为障碍物。图中用#DETOUR标出了绕路结点。
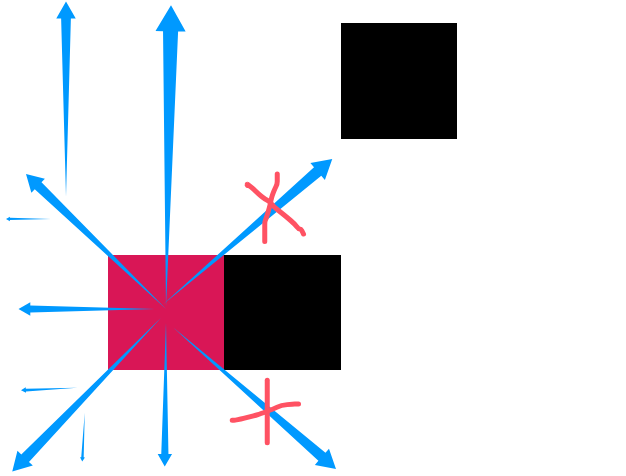
图中实际的最优路径应该是蓝色箭头标出的这一条,然而算法实际的搜索是按黄色箭头标出的方向进行的。
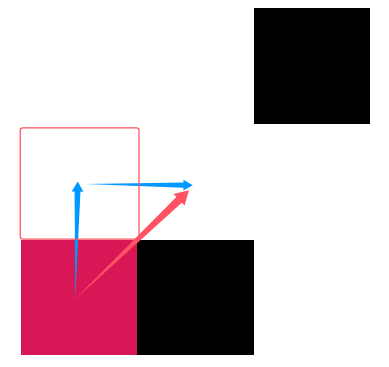
🤔 从图中我发现,因为发生了绕路,算法原本的搜索策略没法保证找到最优路径。应当在绕路结点这里额外进行一些搜索,比如图中在 #DETOUR_2 这里需要沿着蓝色斜箭头(平行于原本的搜索方向,黄色斜箭头)这个方向进行搜索。
💡 因此,需要把绕路结点也加入 open_list,并强制其方向平行于原本的搜索方向(L306),以检查可能被忽略的关键结点。
- 这里“加入
open_list”只是临时加入,详见第 6 节。
说的简单,实现起来还是要绕几个弯子的。
迎面而来的问题是——怎么给绕路结点指定父结点? (路径依靠于父结点的链接来构建)
-
上图中
#DETOUR_2结点左侧的结点是一个跳点,是实际存在的结点,可以直接将其作为#DETOUR_2的父结点。(对应_find_directions中的处理) -
在往一个方向寻找跳点的过程中(
_jump方法),如果碰到对角障碍物,如下这种情况: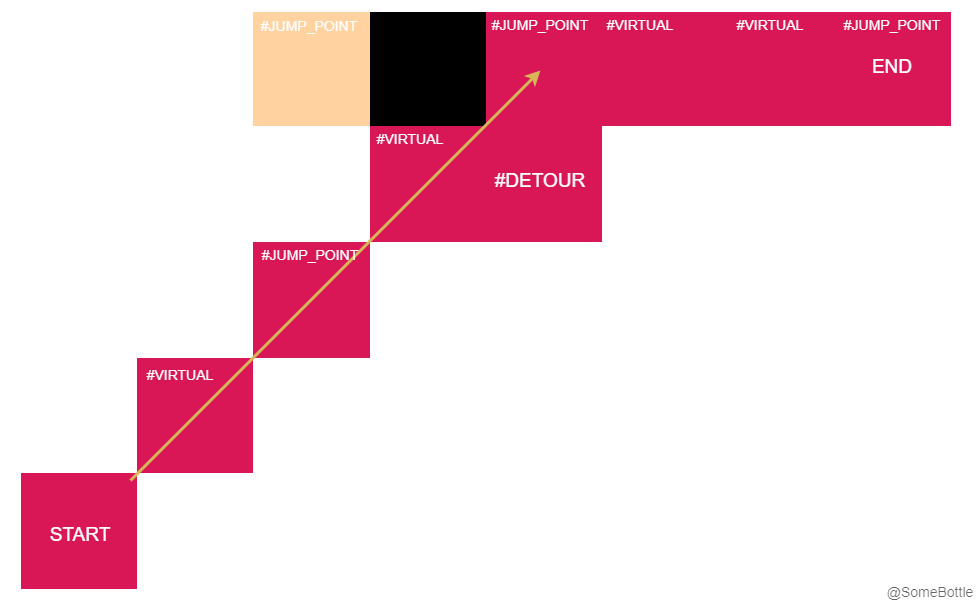
黄色箭头为其中一个跳点搜索方向;#JUMP_POINT标记的为跳点;#VIRTUAL标记的为实际上不存在的虚拟结点;#DETOUR为绕路结点;黑色块为障碍物;黄色块为open_list结点;红色块为最后求解得到的路径。💡 图中这里的绕路结点
#DETOUR左方是没有实际的结点的,需要在其左侧添加一个父节点,并将这个父节点的父链接连接到路径(黄色箭头这条线)上的上一个跳点(L145)。这样一来就能求解得到和 A* 算法一致的路径代价了。
src/problems/generator.py中的generate_partial_ring_problem方法src/problems/draw.py中的draw_problem方法src/problems/problem.py中的Problem.from_matrix静态工厂方法
上面几个方法都有一个 close_diagonal_obstacles 参数,默认为 False。
-
当这个参数为
True时,会对图像进行平滑操作,去除对角障碍物,示例如下:
🤓☝️ 初始化算法对象时如果指定 diagonal_obstacles=False,算法执行过程中就可以穿过对角障碍物,这种情况下你可以预先用 close_diagonal_obstacles=True 消除掉所有对角障碍物,没有对角障碍物,diagonal_obstacles 选项其实就没用了。
上面提到将绕路结点“加入”到 open_list 中。
最开始我在实现 a_star_jps_detour_fixed 这部分算法时,为了图方便,让绕路结点以和其他结点一样的方式加入 open_list,即在加入前检查 open_list 中是否已经有相同坐标的结点,如果有则进行比较,若待加入结点更优则进行替换。
这样做,在障碍物少的图中还看不出端倪,但是一旦障碍物多起来且随机分布起来(比如用 generate_random_problem(150, 80, 0.7) 生成的),很明显 JPS 算法求解得到的路径代价比 A* 要大。
😩 被这个问题折磨了一下午后我终于发现,绕路结点“加入”到 open_list 中是有诀窍的:
- 设绕路结点所在坐标为
$(x_d,y_d)$ 。 - 绕路结点不需要进行任何检查,直接加入
open_list,但是不标记$(x_d,y_d)$ 存在于open_list中。- 我的实现是用优先队列(小根堆)来存储开放列表中的待处理结点,另外用字典去标记已经加入开放列表的结点坐标。这里就直接把绕路结点加入堆,而不在字典中存储其坐标。
- 绕路结点被从
open_list取出后,不加入closed_list。
即把绕路结点当开放列表中的临时结点处理,其不应该决定到达 closed_list),亦不应该影响算法中其他结点加入 open_list 的过程(不标记 open_list 中,因为可能有其他坐标为
💡 绕路结点只是提示算法可能的新关键路径,不应该和原算法其他结点发生冲突。
很尴尬的是,修正后的 JPS 算法在有大量随机障碍物的图中求解速度要慢于 A*。
- 虽然 JPS 扩展的结点数量比 A* 少了很多,但是 JPS 寻找跳点的开销其实也不可小觑...尤其是在障碍物比较复杂的图中。
(⌒‿⌒)つ:你可否知道一个叫 JPS+ 的优化版本?
∑( ̄[] ̄;):咱这回还是暂时先不折腾了吧,以后再说啦~
本来这只是个简单的算法课程大作业的,但是当我绞劲脑汁把 JPS 算法复现出来后,这个事情的性质就变了,(✧∀✧)🔥 我折腾魂又燃起来了 !
于是就顺便把绕路和相应的修正策略实现都写了一下,看到这些算法能顺利跑起来,真的是成就感满满!
- Harabor D, Grastien A. Online graph pruning for pathfinding on grid maps[C]//Proceedings of the AAAI conference on artificial intelligence. 2011, 25(1): 1114-1119.
- Duchoň F, Babinec A, Kajan M, et al. Path planning with modified a star algorithm for a mobile robot[J]. Procedia engineering, 2014, 96: 59-69.
- Harabor D. Fast pathfinding via symmetry breaking[J]. Aigamedev Com, 2012.
- https://zerowidth.com/2013/a-visual-explanation-of-jump-point-search/
- https://hakuya.me/algorithm/findpath/JPS%E7%AE%97%E6%B3%95%E5%88%86%E4%BA%AB/