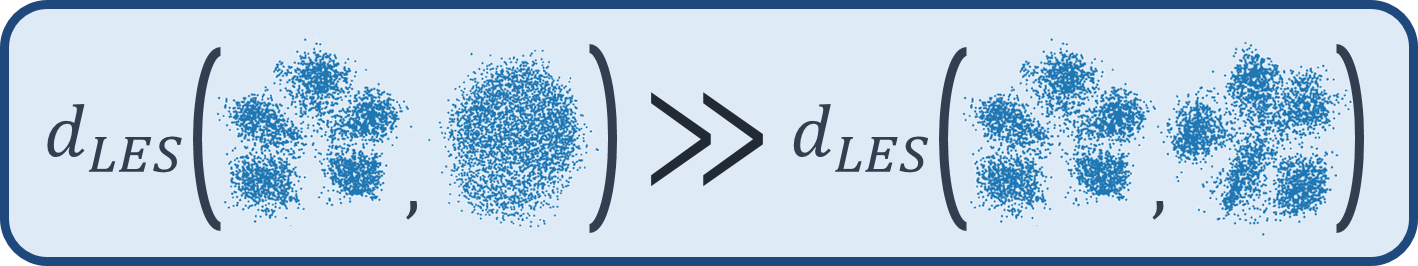Log-Euclidean Signatures for Intrinsic Distances Between Unaligned Datasets

Python implementation of the LES distance and examples from the paper. LES is an intrinsic geometric measure for comparing unaligned datasets of different dimensions and domains.

Prerequisites

Numpy
SciPy
Matplotlib
Optional packages for clustered data usage example: scikit-learn
Optional packages and repositories for comparisons with other algorithms:
- IMD [1] - clone and place the msid folder in the current folder.
- TDA: H0, H1 and H2 bottleneck distances, requires persim , ripser.
- GS [2] - clone and place the gs folder in the current folder.
  Requires GUDHI and Cython.
- GW [3] - requires pot.

The code was tested with python 3.8 and 3.9

Usage example of LES

Distances between multi-cluster and single-cluster datasets of different dimensions

import numpy as np
import sklearn.datasets as skld
from les.les import les_desc_comp, les_dist_comp
   
np.random.seed(1)
x1 = skld.make_blobs(n_samples=1000, centers=5, n_features=10)[0]
x2 = skld.make_blobs(n_samples=1000, centers=5, n_features=9)[0]
x3 = skld.make_blobs(n_samples=1000, centers=1, n_features=10)[0]
  
SIGMA, NEV, GAMMA = 2, 200, 1e-8     
les_desc_x1 = les_desc_comp(x1, SIGMA, NEV, GAMMA)
les_desc_x2 = les_desc_comp(x2, SIGMA, NEV, GAMMA)
les_desc_x3 = les_desc_comp(x3, SIGMA, NEV, GAMMA)
    
print('LES(x1{5 clusters}, x2{5 clusters})=',les_dist_comp(les_desc_x1, les_desc_x2))
print('LES(x1{5 clusters}, x3{1 cluster})=',les_dist_comp(les_desc_x1, les_desc_x3))
print('LES(x2{5 clusters}, x3{1 cluster})=',les_dist_comp(les_desc_x2, les_desc_x3))

Running the tori example (Figure 1 in the paper)

python les/main_tori.py

By default the code compares LES only with our implementation of IMD (our approach) to reduce run-time and code dependencies. To compare with additional algorithms that were mentioned in the paper, specify the algorithm names in main_tori.py, ALGS2COMPARE, and follow the installation instructions of each package in the prequisites above. Note that the topological data analysis methods (tda) and Gromov-Wasserstein distance (gw) require significantly longer run-times.

References