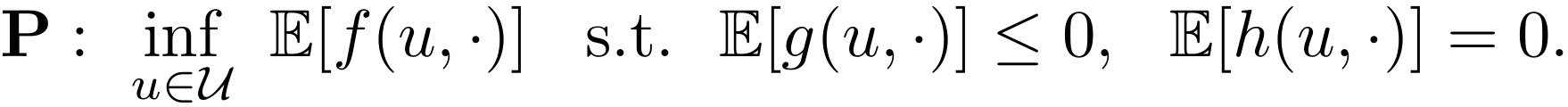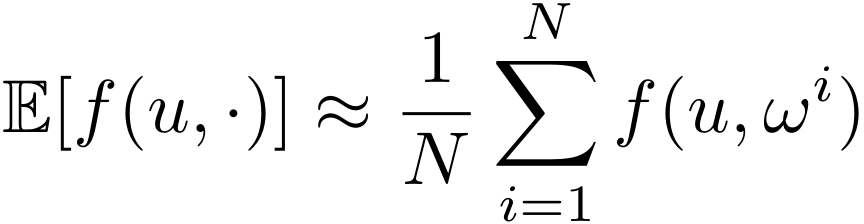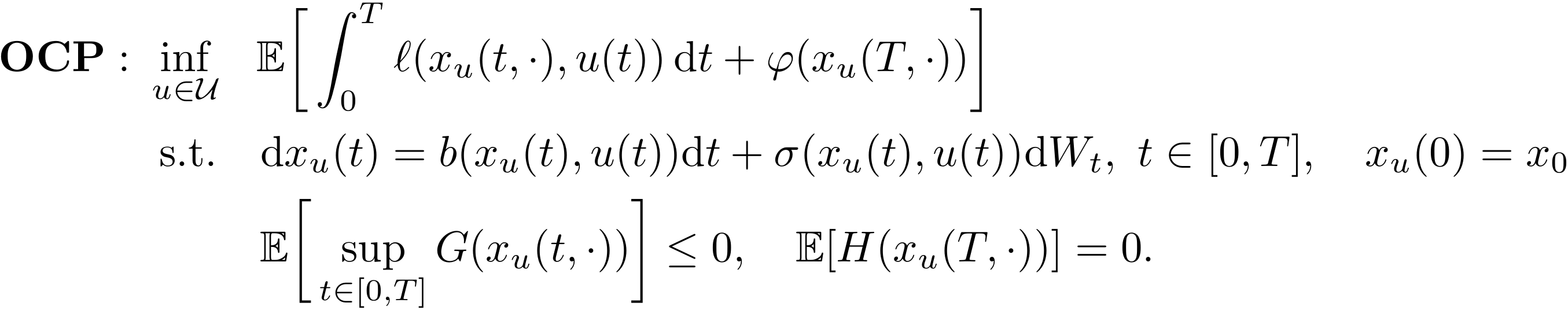Code to reproduce numerical results in T. Lew, R. Bonalli, and M. Pavone, "Sample Average Approximation for Stochastic Programming with Equality Constraints," SIAM Journal on Optimization, 2024. A preprint is available at https://arxiv.org/abs/2206.09963.
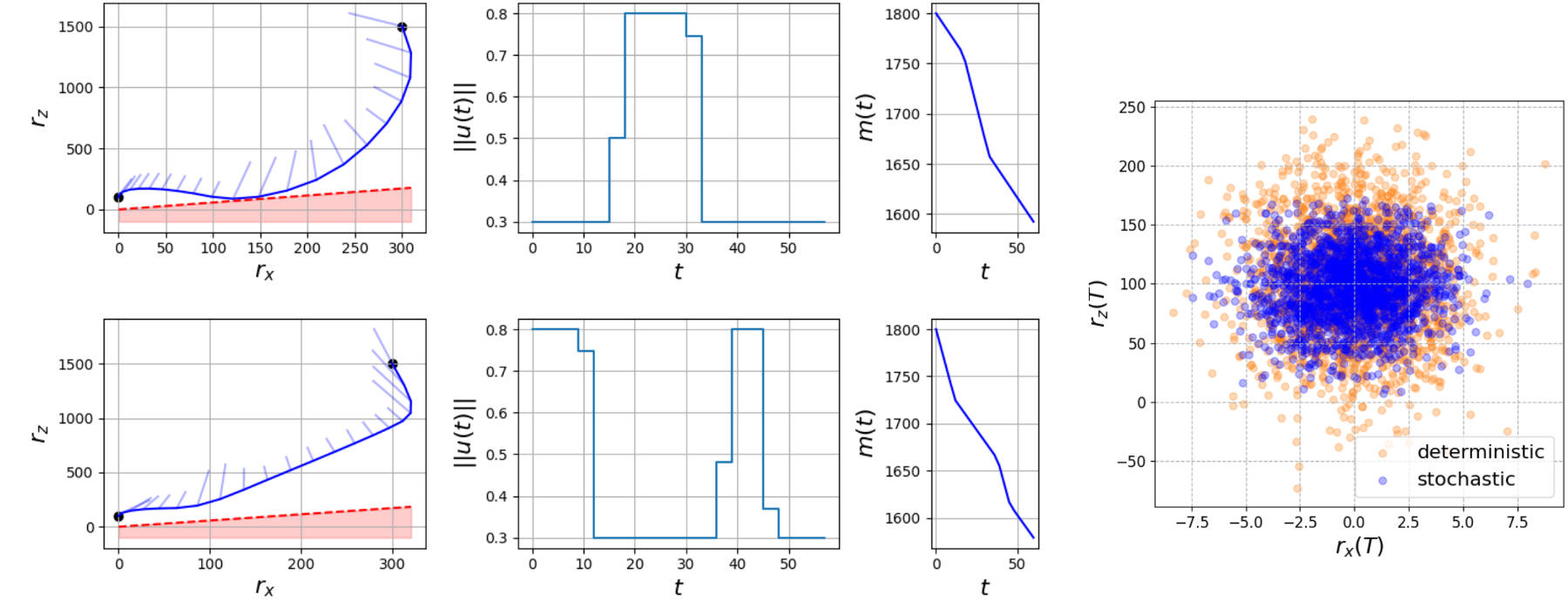
Mars rocket-powered descent results.
Requires Python>=3.6. All dependencies (i.e., numpy, cvxpy, and matplotlib) can be installed by running
pip install -r requirements.txtTo reproduce the benchmark results (Section 6.1), run
python benchmark_main.pyExecuting the script may take a long time. It can be run on different machines in parallel by specifying a subset of problems to solve (python benchmark_main.py --programs_to_solve program_6,program_27) and later plotting the results (python benchmark_main.py --dont_compute_true_solutions --dont_compute_saa_solutions).
For an example of trajectory optimization for a robotic manipulator, run
python manipulator.pyTo reproduce the stochastic optimal control results (Section 6.2), run
python mars_powered_descent.pyThis last implementation is short thanks to CVXPY which easily interfaces with popular solvers such as ECOS. This implementation is not optimized for speed and could be speeded up by (1) directly interfacing with the solver, (2) exploiting the sparsity of the problem (see, e.g., OSQP), (3) parallelizing computations on a GPU, etc.