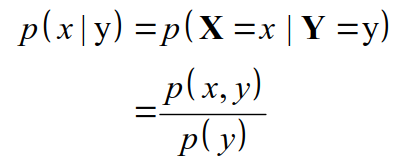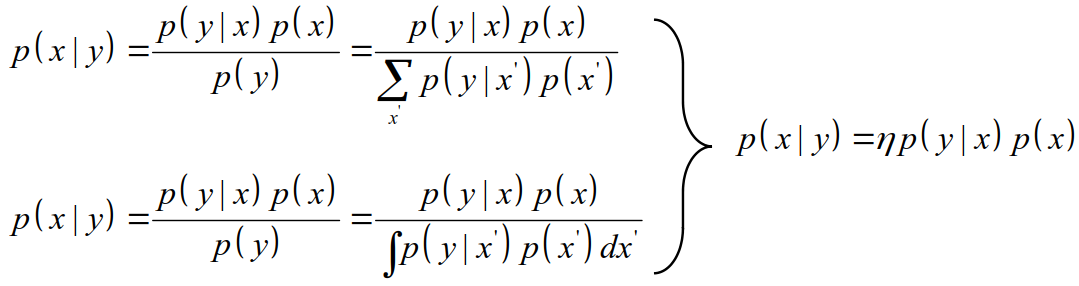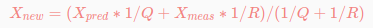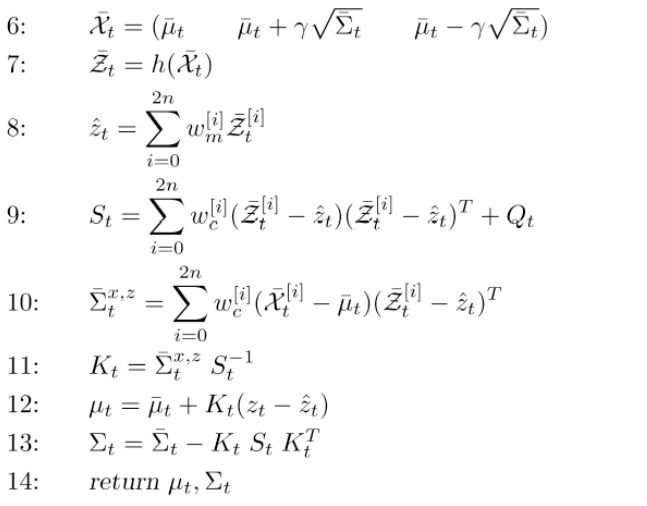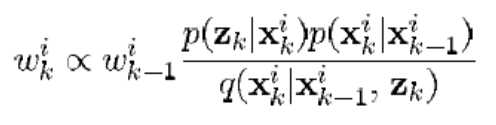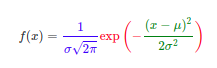/ProbabilisticFilter

Probabilistic filter

Primary LanguageC++

Probabilistic Filter

  • Sungwook LEE(joker1251@naver.com)
    • ALL Authority to Sungwook LEE
    • 모든 소스 코드는 c++로 직접 작성함

Pre requirements

  • Install Eigen3
    • C++에서 Matrix 연산(dot, product, eigen, SVD...)을 쉽게 할 수 있도록 도와주는 오픈소스 라이브러리
    • ubuntu20.04: sudo apt install libeigen3-dev
      • 윈도우용도 있으니, 참고하여 설치
    • 설치 확인: dpkg -L libeigen3-dev
    • header: #include "Eigen/Dense"
    • compile flag: g++ $(pkg-config --cflags eigen3) file.cpp

Reference

Before Reading...,

  • 아래의 수식은 Bayes Filter의 수식으로, Bayes Filter는 Bayes Rule 에 Marcov Process를 결합하여 Recursive하게 풀어낸 것이다.
  • Bayes Filter, Kalman Filter, Non-linear Kalman, Particle Filter 는 모두 아래의 수식을 바탕으로 전개되었다. 하여서, 아래 수식을 손으로도 써보며 반드시, 제대로 느끼는 것(?)이 중요하다.
  • Modern Filter Theory의 모든 것이 Bayes Rule에서 부터 시작된다.

1. Bayes

  1. In the beginning ...

    • Total Probability Theorem
    • Conditional Probability (Likelihood)
    • Bayes Rule

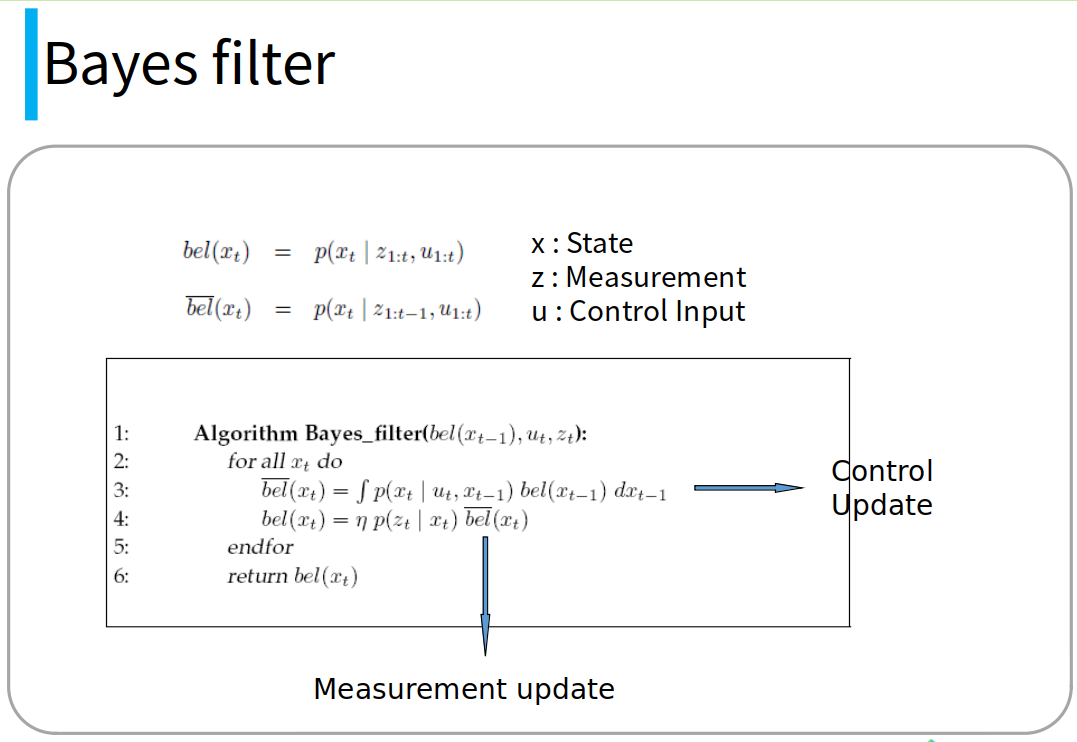
  2. Bayes Filter (수식 매우 중요)

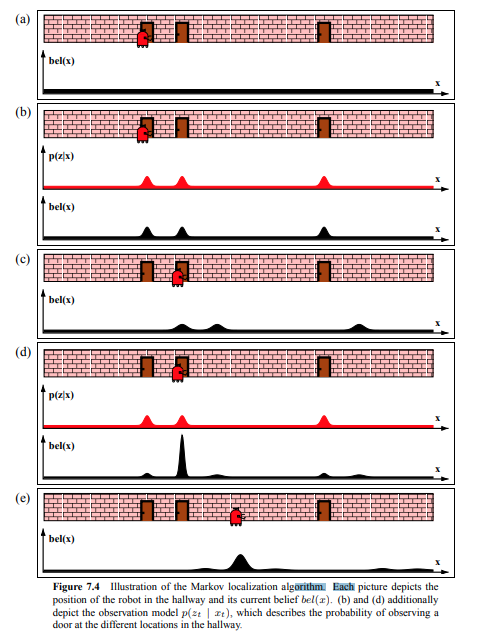
    • Bayes Rule에 Marcov Process + Recursive 을 부여하여 Belief를 Recursively Update!

  3. ILLUSTRAION OF MARKOV

  4. Lecture Practice

  5. Naive Bayes Filter Review

    • 베이즈 필터, 칼만 필터, 파티클 필터의 입력에 의한 predict, 관측에 의한 update 단계에서의 bel=covariance는 정확히 위의 그림과 같이 움직인다.

    • 예측 단계에서는 covariance가 움직이고(+더하기 불확실성 증대), update 단계에서는 covariance가 보정된다.(x곱하기, 확률은 1보다 작은값이어서 곱하면 작아진다. 불확실성 감쇄)

2. Kalman

  • Bayes 필터는, 모든 state에 대한 확률 적분값(Total Probability Theorem)을 구하는 것이 현실적으로 불가능하다.
    • 칼만필터 등장의 이유
  • 이를 실현 가능한 표현형으로 풀어낸 것이 칼만필터이다. 확률분포함수를 가우시안 확률분포로 하여 분포를 평균과 분산으로만 나타내어 식을 유도하였다.
  • 모델의 분산과, 센서값의 분산, 이 둘을 이용해서 new_X를 만들어 내는 과정이 칼만필터

  1. Assumption: Linear Model, Noise is follow Gaussian

    • Linear여야지만, 칼만 필터의 Equation을 유도할 수 있고 (예를 들어, A'PA+Q) 가우시안 이여야지만 확률분포를 임의의 함수가 아닌, 평균과 분산으로만 기술할 수 있게 된다.

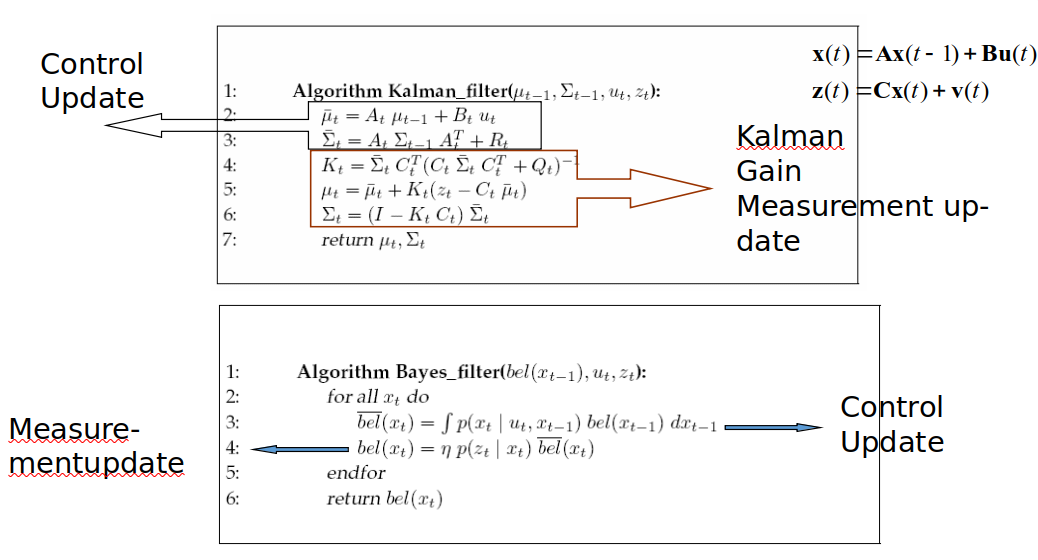
  2. Derivation

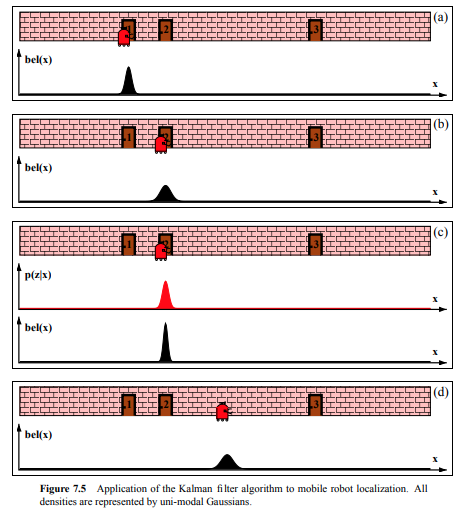
  3. ILLUSTRAION OF KALMAN

  4. Lecture Practice

3. Nonlinear Kalman

  1. Extended Kalman Filter

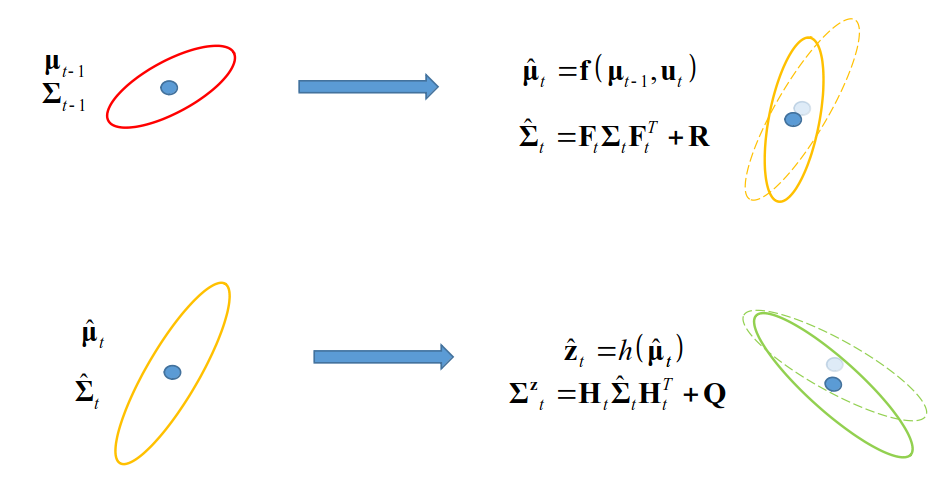
    • 선형화(Jacobian)을 통한 [Covariance, State] Linear Expansion

  2. Defivation

  3. Lecture Practice(EFK)

  4. Unscented Kalman Filter

    • 비선형성이 크면 클수록, EKF의 성능은 저하된다.
    • Sigma Points인 (1+2N)개 포인트 만으로도 로 가우시안을 평가할 수 있다. Unscented Transform
      • N은 State의 개수를 의미함
    • 점들은 어떻게 고를까?
      • Unscented Transform 에 정의대로 1+2N개를 고른다.

  5. Lecture Practice(UKF)

  6. 비선형 칼만 한계

    • 가우시안 노이즈를 따르지 않는 문제에서, 어떻게든 선형화(Extended), 선형평가(Unscented) 방식으로는 필터의 성능은 나오지 않는다.
    • 비선형을 무조건 선형화(Relaxation)할 수 있는 것이 아니다.
    • 베이즈 필터는 적분에 한계가 있었기 때문에.., 가우시안 분포를 가져와 칼만필터를 만든 것
      • 칼만필터: Parameteric Approach: N(0, Sigma^2)
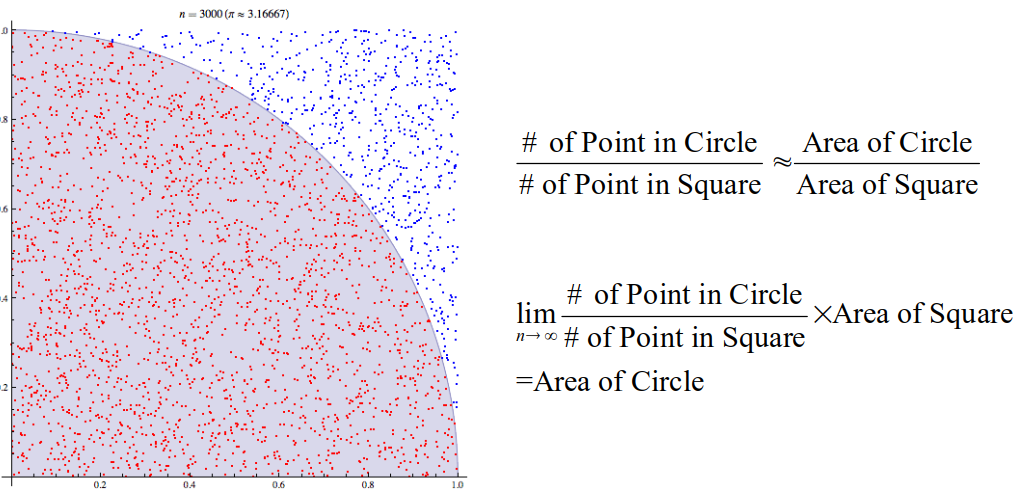
    • 다른식의 접근법: Non Parameteric Approach: 가우시안 함수 등을 사용하지 말고 적분해야 하는 샘플의 개수를 유한개(몬테카를로 Sampling)로 하여 적분값을 평가하자
      • 파티클필터 등장의 이유

4. Particle Filter

  1. 확률필터 리뷰

    • 알고싶은 정보: $P(x_t|u_{1:t}, z_{1:t})$
    • 어떻게 하면 알 수 있을까?, 마르코프 프로세스와 재귀적 구조를 사용하여 구하자.
      • 재귀적 구조로 belief update

  2. 칼만필터 접근법 한계 리뷰

    • 리니어야하고, 노이즈는 가우시안 분포를 따라야 한다.
    • 근데, 가우시안 분포를 따르지 않는다면?, 더 이상 $N(\mu,\sigma^2)$ 의 파라미터인 $\mu$, $\Sigma$로 식을 derivation 할 수 없다.
    • 칼만필터의 접근법을 Parameteric Approach 라고 한다.
    • 가우시안 함수를 사용치 말고 샘플의 개수를 유한개로(몬테카를로 샘플링)하여 적분값을 평가하자. (Non Parameteric Approach)

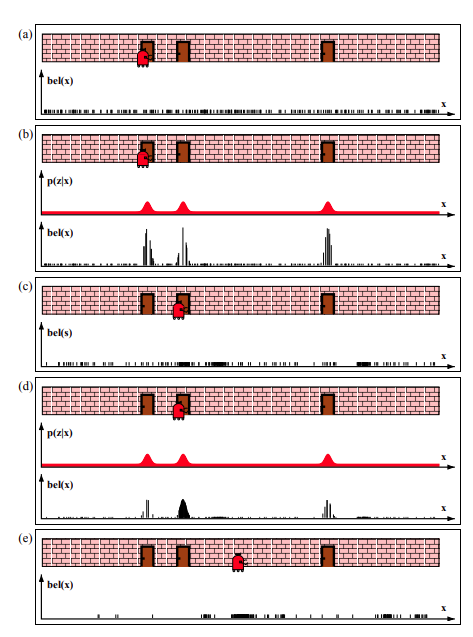
  3. 파티클필터

    • 컨셉
      • 분산이나, 기대값을 어떤 모형 함수(예를들어, 가우시안)로 구하지 않고, 직접 구하자
      • 모든 정보를 가지고 분산을 평가할 것이 아니라, 아는 정보만을 가지고 분산을 평가하자
      • 원의 넓이는 개수의 파티클로도 유사하게 구할 수 있다.

  4. ILLUSTRATION OF PARTICLE FILTER

  5. STEP

    • Predict(control): Sampling
    • Update(measurement): 관측값과 확률매칭하여 웨이트 갱신

  6. 구현의 두가지 방식

    • 일반적으로 SIR을 사용함
    1. SIS(Sequential Importance Sampling): 파티클 하나가 웨이트 하나를 가짐으로써, 웨이트가 높은 파티클이 잘못 수렴되었을때, 추정 결과값이 이상해지는것을 막을 수 없다. (웨이트의 크기에 따라 입자 선택)
    2. SIR(sequential Importance Resampling): Resampling Wheel 과정을 통해 이전 스텝에서의 웨이트를 기준으로 파티클을 할당하고 초기화함으로써(할당된 파티클의 개수가 웨이트의 크기라고 볼 수 있음) 파티클을 새롭게 분포시킴으로써, 잘못된 결과값에 수렴되지않게끔 -> 일반적으로 우리가 부르는 파티클 필터 (참고(로컬라이제이션): particleLocalization.cpp)

  7. Lecture Practice(Particle Filter: SIR)

끝