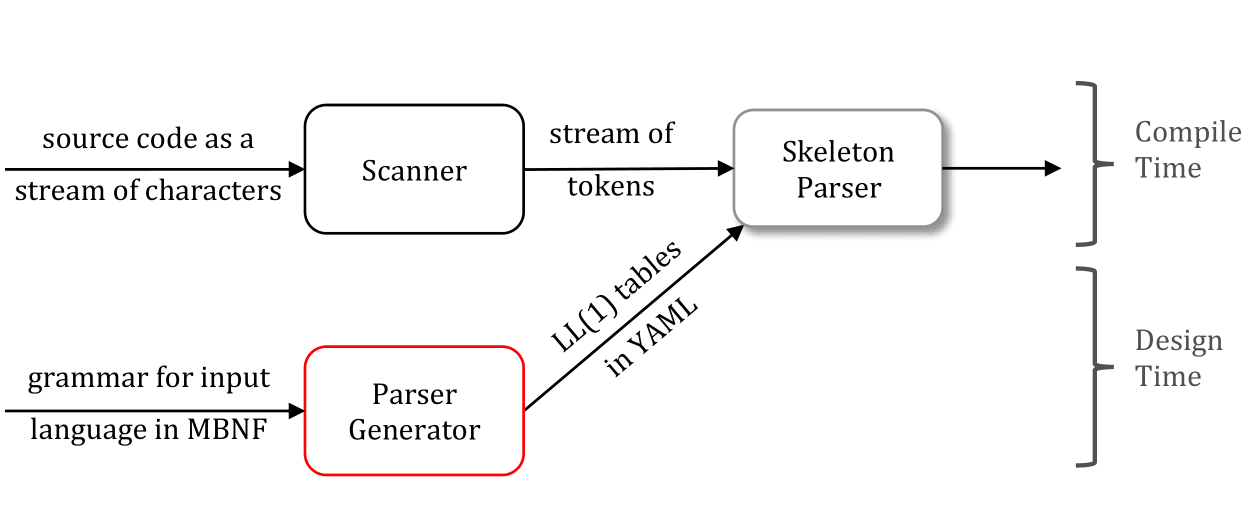
In this project, you will implement a LL(1) parser generator. Your program takes as input a grammar in the Modified Backus-Naur Form (MBNF) Section 2, and computes the First, Follow, and Next sets for the grammar. You must support output in both a human-readable format Section 3.2 as well as LL(1) tables in the YAML format Section 3.3. You can test the correctness of your parser generator using the skeleton parser Section 1.2, which accepts YAML tables as input.
To place your program in context, Figure 1 diagrams a compiler’s front end, including the stages that comptuation costs are incurred in. The parser generator is responsible for taking the grammar and producing a set of tables. You are not responsible for tokenizing the input to the skeleton parser: that is the job of the scanner. You are responsible for attempting to create the LL(1) parsing tables. This may fail for a number of reasons: the input file given may not exist, the grammar contained in the file may be invalid, or the grammar may not be LL(1). You should produce appropriate error messages for every case.
Your code must compile on the xena machines, using a Makefile in that directory, to an executable named llgen in that directory. If you are using a programming language that does not produce an executable, include an script named llgen instead. Your program must implement the following command line arguments.
-h Print a list of valid command-line arguments and descriptions to `stdout` and quit.
-t Print the LL(1) table in YAML format, as specified below. You should
produce no output to `stdout` other than the LL(1) table. If there is an error,
print an informative error message to `stderr`. In specific, if the input
grammar is not LL(1), then print which productions created the problem to
`stderr`.
-r If supported, attempt to transform a non-LL(1) grammr into an LL(1) grammar by
removing left-recursion and factoring common prefixes. This is entirely optional.
-w Use a worklist optimization of the fixpoint algorithms.
Error messages for invalid arguments or an invalid file must be reasonable and printed to stderr.
You should include a BUILD.md file that provides directions for building and invoking your program. Include both the required arguments and any additional arguments that your program supports.
A number of tools and reference files are available in the repository. They include:
-
grammars: A folder containing a number of sample grammars, as well as several outputs and test cases. There is one text file with a sample human-readable output. You do not have to adhere to this output precisely, and the order of the tables does not matter. -
skeletonParser.rb: A skeleton parser you can use to test your generated code. Run with./skeletonParser.rb -d <table file> <input file>.
Your parser generator will need to understand an MBNF grammar for the compiler’s input language. You will construct a scanner and a hand-coded, recursive-descent parser for MBNF to serve as the front half of your parser generator. Your recursive-descent parser will build an internal representation for the grammar of the input language. The table below lists the grammar for Modified Backus-Naur Form, with terminal symbols written in all uppercase letters. Your parser generator will accept as input a description of the parser’s input language in this grammar. Note that the MBNF grammar, as stated, relies on left recursion; before building your parser, you must transform the grammar for MBNF to make it suitable for a top-down, recursive-descent parser.
| 1 | Grammar | ProductionList | |
| 2 | ProductionList | ProductionSet SEMICOLON | |
| 3 | ProductionList ProductionSet SEMICOLON | ||
| 4 | ProductionSet | SYMBOL DERIVES RightHandSide | |
| 5 | ProductionSet ALSODERIVES RightHandSide | ||
| 6 | RightHandSide | SymbolList | |
| 7 | EPSILON | ||
| 8 | SymbolList | SymbolList SYMBOL | |
| 9 | SYMBOL |
modified
| 1 | Grammar | ProductionList | |
| 2 | ProductionList | ProductionSet SEMICOLON ProductionList | |
| 3 | EPSILON | ||
| 4 | ProductionSet | SYMBOL DERIVES RightHandSide ProductionSet' | |
| 5 | ProductionSet' | ALSODERIVES RightHandSide ProductionSet' | |
| 6 | EPSILON | ||
| 7 | RightHandSide | SymbolList | |
| 8 | EPSILON | ||
| 9 | SymbolList | SYMBOL SymbolList |
It is important that you understand the difference between the grammar for MBNF, given in this table, and the input grammars that your parser generator accepts as input. The user of the parser generator will provide an input grammars, written in MBNF, for the language that their compiler should accept. Because the parser generator must read the input grammar, which is written in MBNF, the parser generator will include a scanner and a recursive-descent parser for MBNF. Thus, the parser that you write will accept MBNF; when the tables that your program generates are used with the skeleton parser, that skeleton parser will accept the language specified by the input grammar.
In specific, while the MBNF grammar uses uppercase letters for terminal symbols, the input grammar has no such restriction. Example input grammars are available; notice that they use upper and lower case letters freely. In practice, your parser generator can identify terminal symbols because they do not appear on the left-hand side of any production. Any non-terminal symbol will appear on the lefthand side of at least one production.
You will build a scanner for the words in MBNF. You may use regular expressions, scanf, or other string-manipulations functions if you desire. The table below provides the regular expressions for the five token types in MBNF. EPSILON tokens must be surrounded by whitespace: otherwise they are part of of a SYMBOl token. Note that the SYMBOL token is special: the symbols of the input grammar become the indexes into First, Follow, and the Next table. Unlike Project 1, the symbols are not known until run-time, and therefore you cannot use an enum. Thus the scanner will need to build a lookup table of the symbols to enable efficient translation between names and indexes. You are allowed to use a hash function. See EAC2e § 5.1 and Appendix B for advice on implementing hash tables and sets.
| Terminal Symbol | Regular Expression |
|---|---|
| SEMICOLON | |
| DERIVES | |
| ALSODERIVES | | |
| EPSILON |
|
| SYMBOL |
Note that the | in ALSODERIVES is the symbol |, whereas the
Once you have a working scanner, you will transform the MBNF grammar to make it suitable for recursive-descent and build a hand-coded, recursive-descent parser for it. Each non-terminal in the transformed grammar must have a corresponding function in your recursive-descent parser. Your parser should build up an internal representation (IR) of the productions in the input grammar. The IR should be suitable for use in the computation of First, Follow, and Next sets. Look over those algorithms to determine what types of operations your program will perform on the productions and design an appropriate representation. Your parser should build the data structures needed by the table generator.
Your parser generator will then use the information encoded in your representation construct First, Follow, and Next sets. The algorithms for all of these sets are included in Appendix A.
The algorithms for First and Follow are fixed-point computations that do not use worklists: if the set changes for any symbol, then every production is re-evalutated. This is exceedingly inefficient. You should implement modify these algorithms to use a worklist. The worklists should begin with every production. When the set for a symbol changes, add any productions that may be affected by those changes to the worklist. Continue evaluating each production in the worklist until it is empty. The worklist should be a set (it does not need to contain the same production twice). You must implement the non-worklist version of the algorithms first, and revisit them as time allows.
Unless the -t flag is provided, you should the following information to stdout, regardless of whether the input grammar has the LL(1) property or not.
- The productions as recognized by the parser.
- The
Firstset for each nonterminal. You may also print theFirstset for terminals if you desire. - The
Followset for each nonterminal. - The
Nextset for each production.
If the -t flag is provided, your program will further attempt to build an LL(1) parse table from these sets. If the input grammar does not have the LL(1) property, your program should produce an error message that states which productions in the grammar created the problem.
In this case your program should output the information needed to drive the skeleton parser. To parse a string, the skeleton parser needs to know the terminals, nonterminals, EOF marker used in the parse table, error marker used in the parse table, start symbol, productions, and LL(1) parse table. You must output this information in YAML format. An example is provided below, for the grammar
terminals: [a, b]
non-terminals: [B]
eof-marker: <EOF>
error-marker: --
start-symbol: B
productions:
0: {B: [a, B, b]}
1: {B: []}
table:
B: {b: 1, a: 0, <EOF>: 1}Each component of the output must be provided using precisely the name specified, mapping to a precise type of YAML value, as described below. Terminals (terminals) and non-terminals (non-terminals) are lists. The eof marker (eof-marker), error marker (error-marker), and start symbol (start-symbol) must be strings or integers.
The productions (productions) must be encoded as a map of map of lists. Each production is keyed with a unique number. The value of a map containing a single entry, mapping the left-hand symbol to the list of symbols on the right hand side. Productions that have a right hand side of
The final element is the table (table), which is a map of maps, similar to using a nested array to represent a two-dimensional table. The outer map represents the rows; it has keys that are the non-terminals. Each non-terminal maps to another map, in which the keys are the terminals or the EOF marker, and the values are either a production number or the error marker. Every non-terminal, and the EOF marker, should occur in the every row of the table.
The syntax for YAML maps, lists, maps of maps of lists, and maps of maps is provided by example above, but formally described in Appendix B.
The next set for a production
- If
$\epsilon \in First(B_i)$ for every$1 \leq i \leq k$ , then$Next(A \rightarrow B_1 \ldots B_k) = \big(\bigcup_{1 \leq i \leq k} First(B_i)\big) \cup Follow(A)$ - Otherwise, let
$B_n$ be the first symbol where$\epsilon \not \in B_i$ , and$Next(A \rightarrow B_1 \ldots B_k) = \big(\bigcup_{1 \leq i \leq n} First(B_i)\big) \setminus \{ \epsilon \}$ .
Note this expression is an abstraction of part of the process of computing first sets. Involuting these sets into a Next table is left as an exercise for the reader.
The YAML format is very sensitive to proper spacing, so follow the format closely. Map keys must be indented. White space must be spaces or newlines, and must appear after colons (‘:’) and commas (‘,’). Do not use tabs, and newlines should only be used for outer level maps. A map is written
map:
key1: value1
key2: value2List is represented as \[item1, item2, item3\] on a single line. Maps of maps do not require nesting indentation. Instead, they are written:
mapofmap:
key1: {key11: value11, key12: value12}
key2: {key21: value21, key22: value22}A map of map of lists (which here only has a single nested key) is written:
mapoflist:
key1: {nestedKey2 : [item1, item2, item3]}
key2: {nestedKey2 : [item1, item2, item3]}