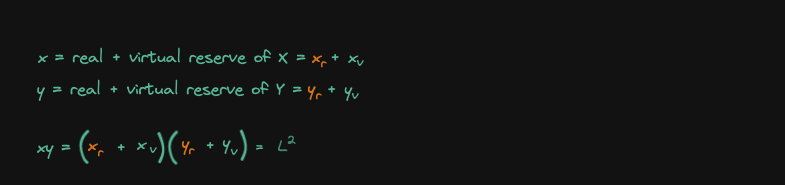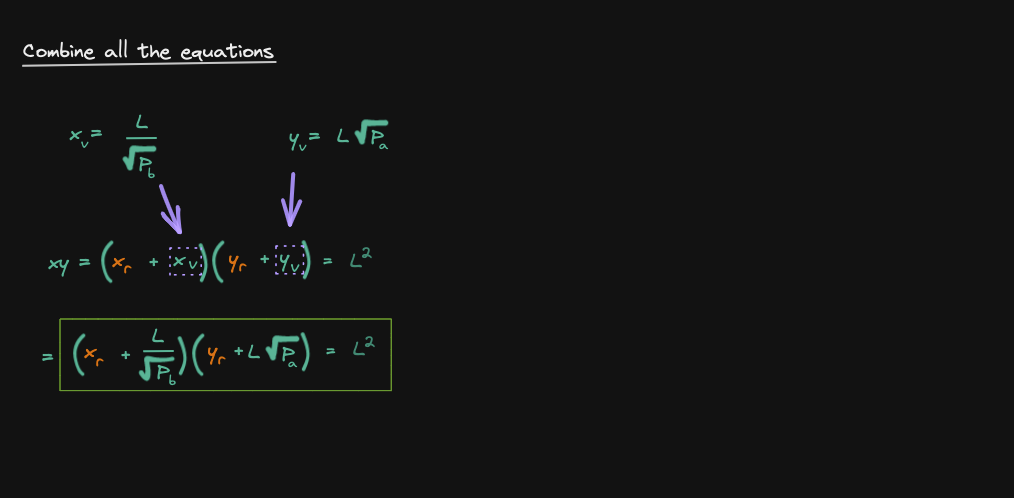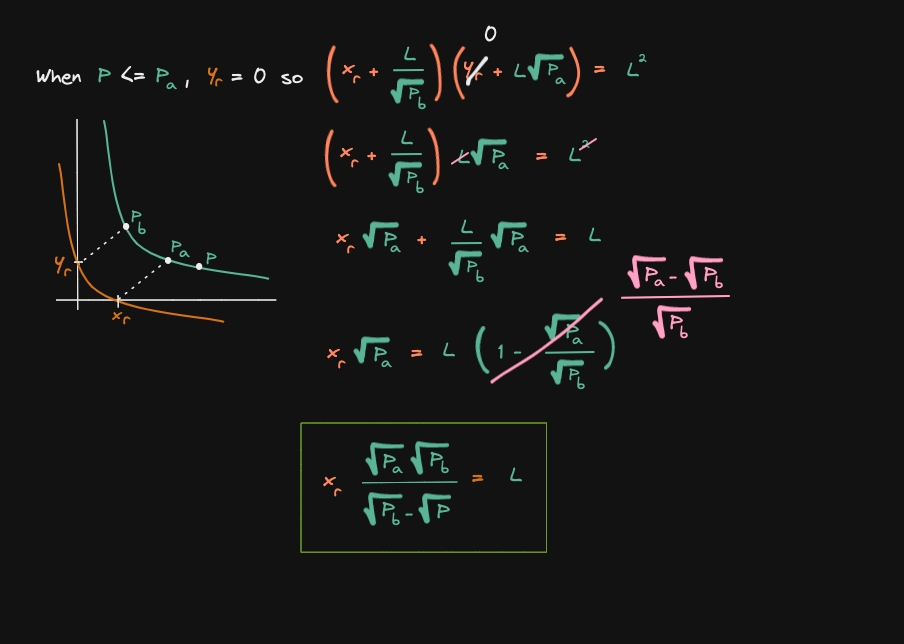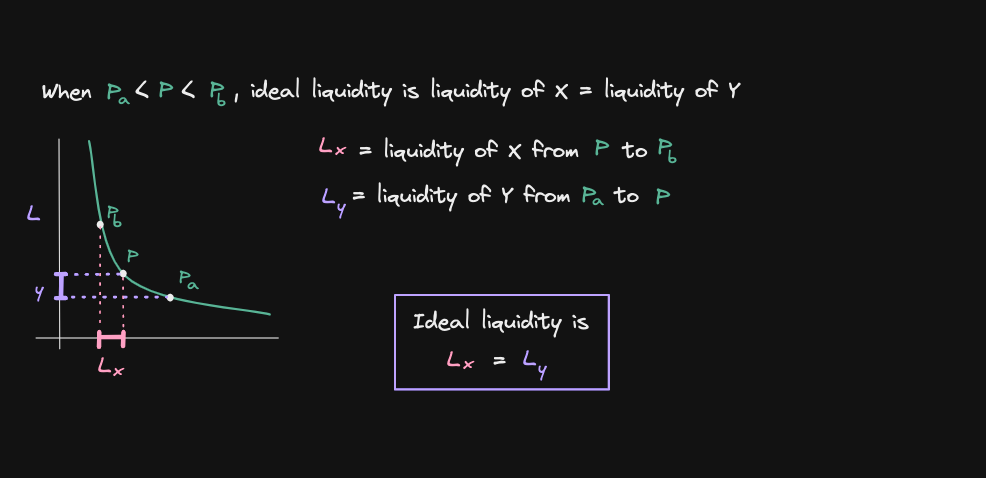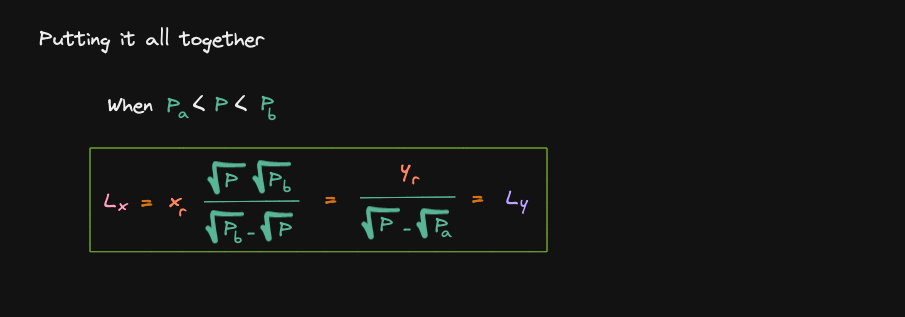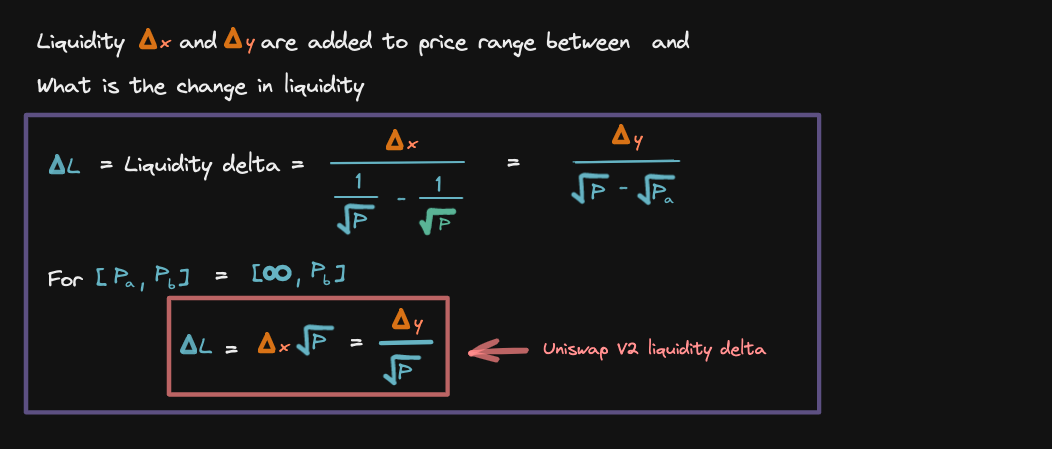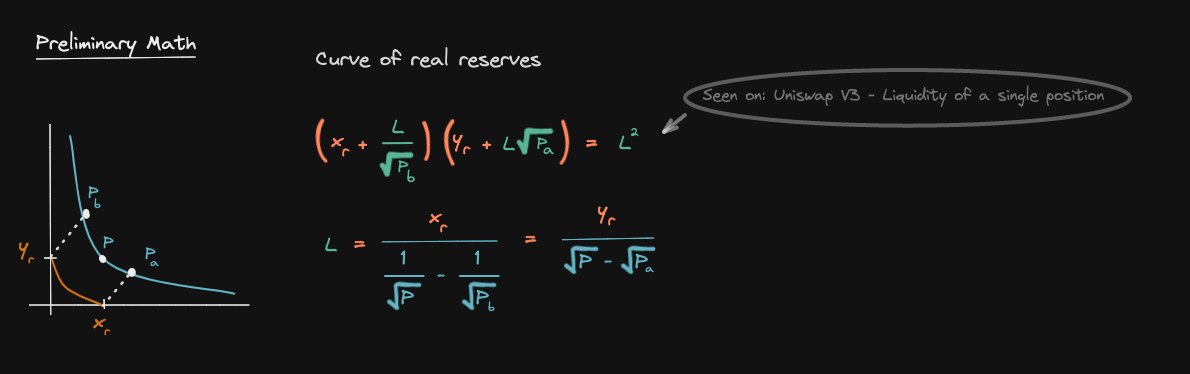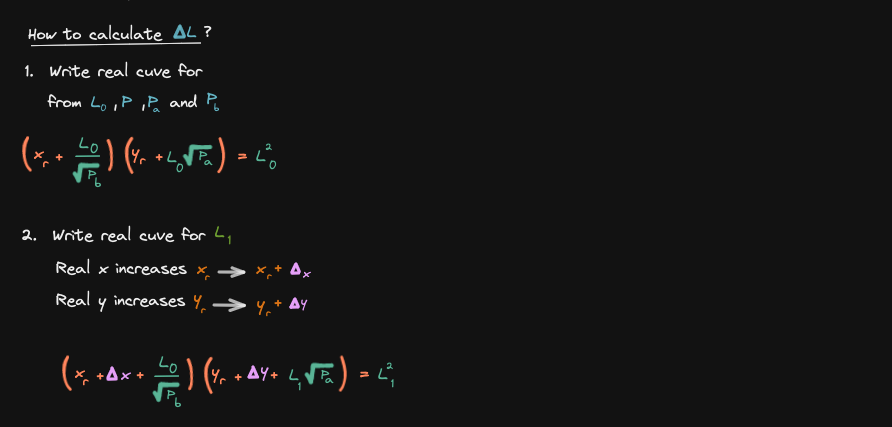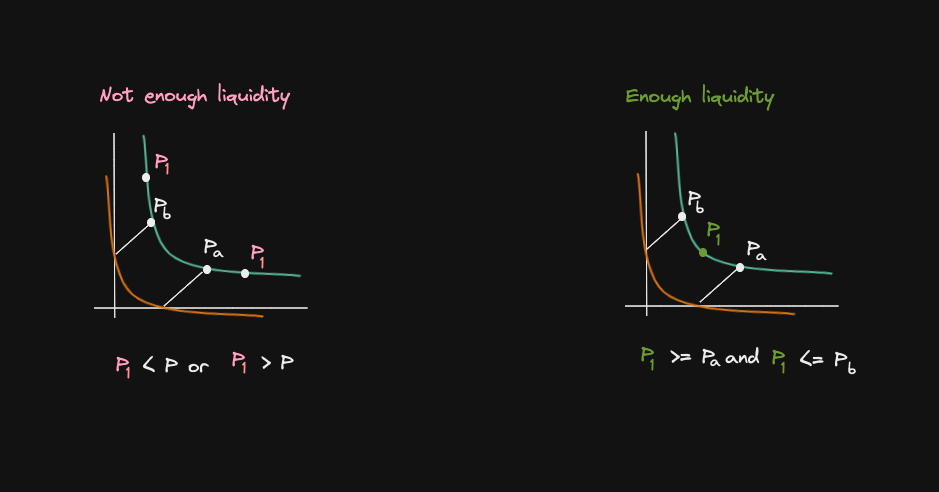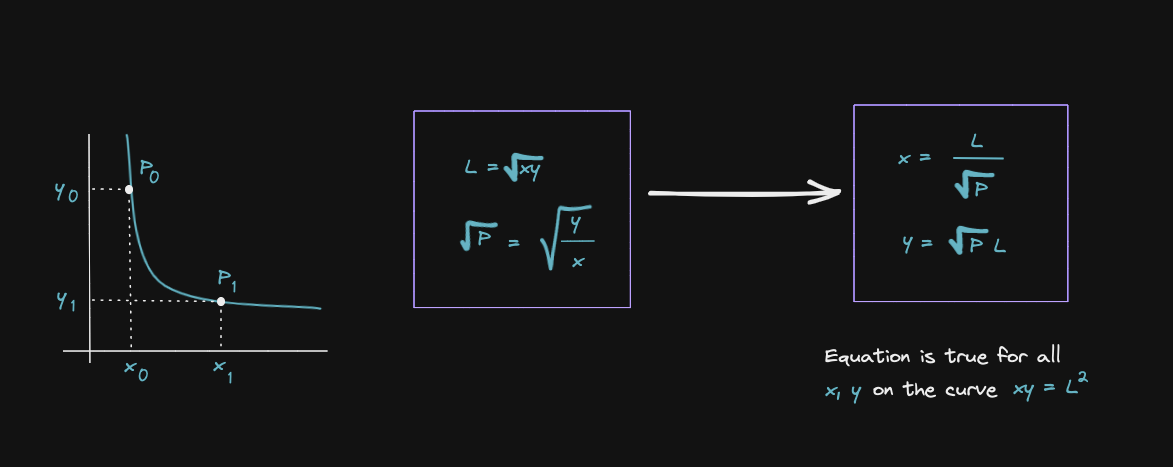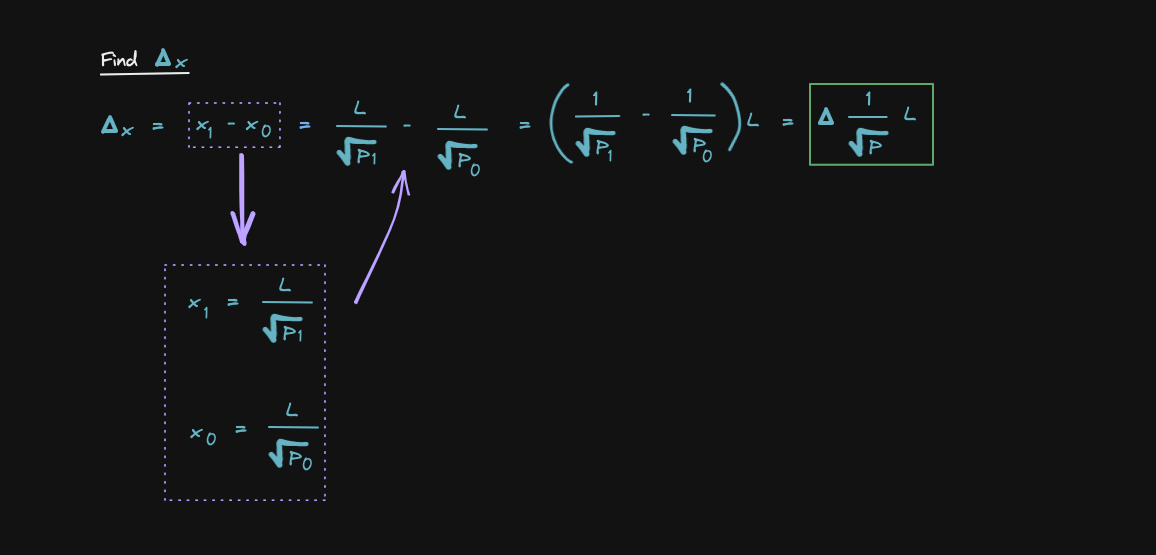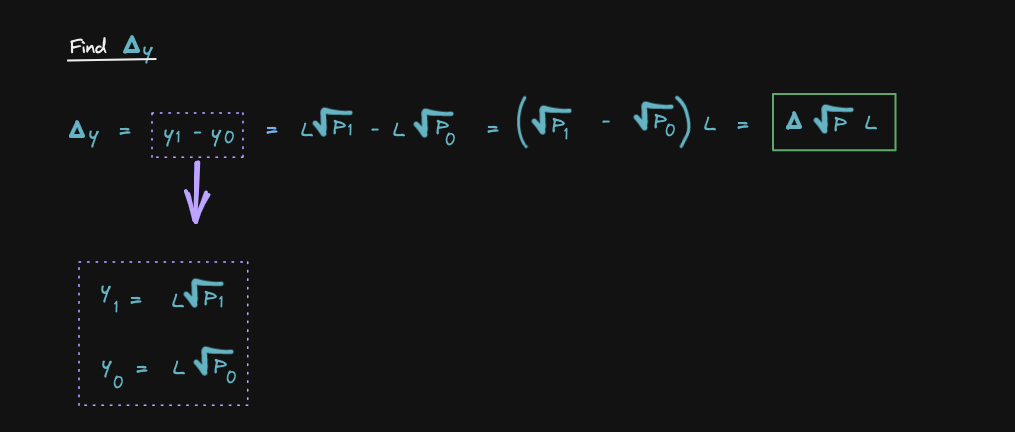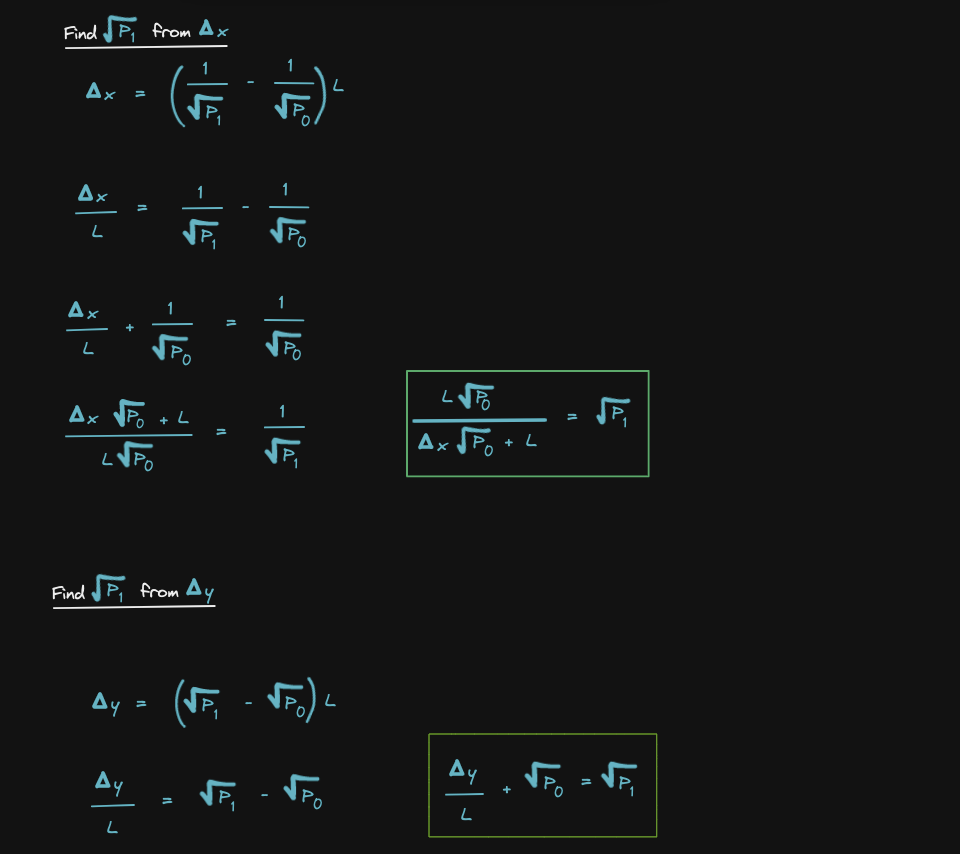/Uniswap-v3

🦄🦄 🦄Single & multi hop swap, add and remove liquidity, flash swap ⚡

Primary LanguageSolidity

Contributors Forks Stargazers Issues MIT License LinkedIn


Logo

Uniswap V3

Uniswap V3
Explore the docs »

View Demo · Report Bug · Request Feature

Table of Contents
  1. About The Project
  2. Getting Started
  3. Usage
  4. Constant Product AMM
  5. Test Single and Multi hop swap
  6. Uniswap V2 Single Hop Swap
  7. Uniswap V3 Multi Hop Swap
  8. Uniswap V3 Curve of real reserves
  9. Test Mint new position
  10. Uniswap V3 Liquidity of a single position
  11. Test Collect fees
  12. Test Increase liquidity
  13. Test Decrease liquidity
  14. Uniswap V3 Liquidity Delta
  15. Uniswap V3 How many tokens to add
  16. Uniswap V2 Add and Remove Liquidity
  17. Uniswap V3 Price of ETH from sqrtPriceX96
  18. Uniswap V3 Tick and sqrtPriceX96
  19. Uniswap V3 Price Change from a Swap
  20. Uniswap V3 Liquidity Price Graph
  21. Uniswap V3 Liquidity Price Graph Example
  22. Uniswap V3 Flash Swap
  23. Uniswap V3 Capital Efficiency
  24. Uniswap V3 Just In Time Liquidity
  25. Forking mainnet
  26. Note
  27. Roadmap
  28. Contributing
  29. License
  30. Contact
  31. Acknowledgments

About The Project

This project shows how to interact with the main functions of Uniswap V3 and derive the equations used in the protocol

(back to top)

Built With

  • Hardhat
  • Ethers

(back to top)

Getting Started

To get a local copy up and running follow these simple example steps.

Prerequisites

  • npm

    npm init

  • hardhat

    npm install --save-dev hardhat

    run:

    npx hardhat

    verify:

    npx hardhat verify --network goerli "contract address" "pair address"

Installation

  1. Clone the repo

    git clone https://github.com/Aboudoc/Uniswap-v3.git

  2. Install NPM packages

    npm install

  3. Dependencies

     npm add @uniswap/v3-periphery @uniswap/v3-core

    For openzeppelin contract, we'll need to install first solidity 0.7

    npm i @openzeppelin/contracts@3.4.2

    To fix compiler errors, we'll need to change the compilation settings

(back to top)

Usage

If you need testnet funds, use the Alchemy testnet faucet.

This project shows how to swap, add and remove liquidity

Constant Product AMM

Uniswap V3 is a Constant product AMM (automated market maker) <=> a decentralized exchange where 2 tokens are traded. You can find a deep overview of CPAMM in this repo

Test Single and Multi hop swap

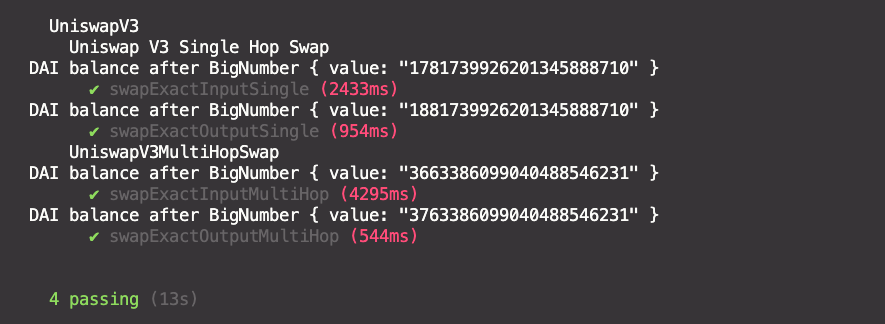
npx hardhat test test/unlock-account.test.js
npx hardhat test test/swapV3.test.js
Test

(back to top)

Uniswap V3 Single Hop Swap

This contract introduces 2 functions to perform single hop swaps on Uniswap V3

exactInputSingle - Sell all of input token. exactOutputSingle - Buy specific amount of output token.

We are interacting with the interface for Uniswap V3 router ISwapRouter

State variables

  1. Address of tokens (2 or 3) and the address of the router
  2. Set interfaces for tokens and router

Function swapExactInputSingleHop

  1. Transfer amountIn from msg.sender
  2. Approve amountIn to router
  3. Set the params by preparing struct ISwapRouter.ExactInputSingleParams
  4. Call exactInputSingle on ISwapRouter (router interface)

Function swapExactOutputSingleHop

  1. Transfer amountInMaxfrom msg.sender
  2. Approve amountInMax to router
  3. Set the params by preparing struct ISwapRouter.ExactOutputSingleParams
  4. Call exactOutputSingle on ISwapRouter and store amount of WETH spent by Uniswap in amountIn (uint)
  5. Refund WETH not spent back to msg.sender
  6. Reset approvals of WETH for router to 0

Uniswap V3 Multi Hop Swap

Swap WETH for USDC and then USDC for DAI.

exactInput - Sell all of input token. exactOutput - Buy specific amount of output token.

We are interacting with the interface for Uniswap V3 router ISwapRouter

State variables

  1. Address of tokens and the address of the router
  2. Set interfaces for tokens and router

Function swapExactInputMultiHop

This function will swap WETH for maximum amount of DAI.

  1. Transfer amountIn from msg.sender
  2. Approve amountIn to router
  3. Setup the swapping path
  4. Prepare struct ISwapRouter.ExactInputParams
  5. Execute the trade by calling router.exactInput with the parameters prepared above

Function swapExactOutputMultiHop

This function will swap minimum amount of WETH for a specific amount of DAI.

  1. Transfer amountInMaxfrom msg.sender
  2. Approve amountInMax to router
  3. Setup the swapping path
  4. Call swapTokensForExactTokens on IUniswapV2Router and store the actual amount of token in swapped for token out in amountSwap (uint)
  5. Refund efund WETH not spent back to msg.sender
  6. Reset approvals of WETH for router to 0

(back to top)

Uniswap V3 Curve of real reserves

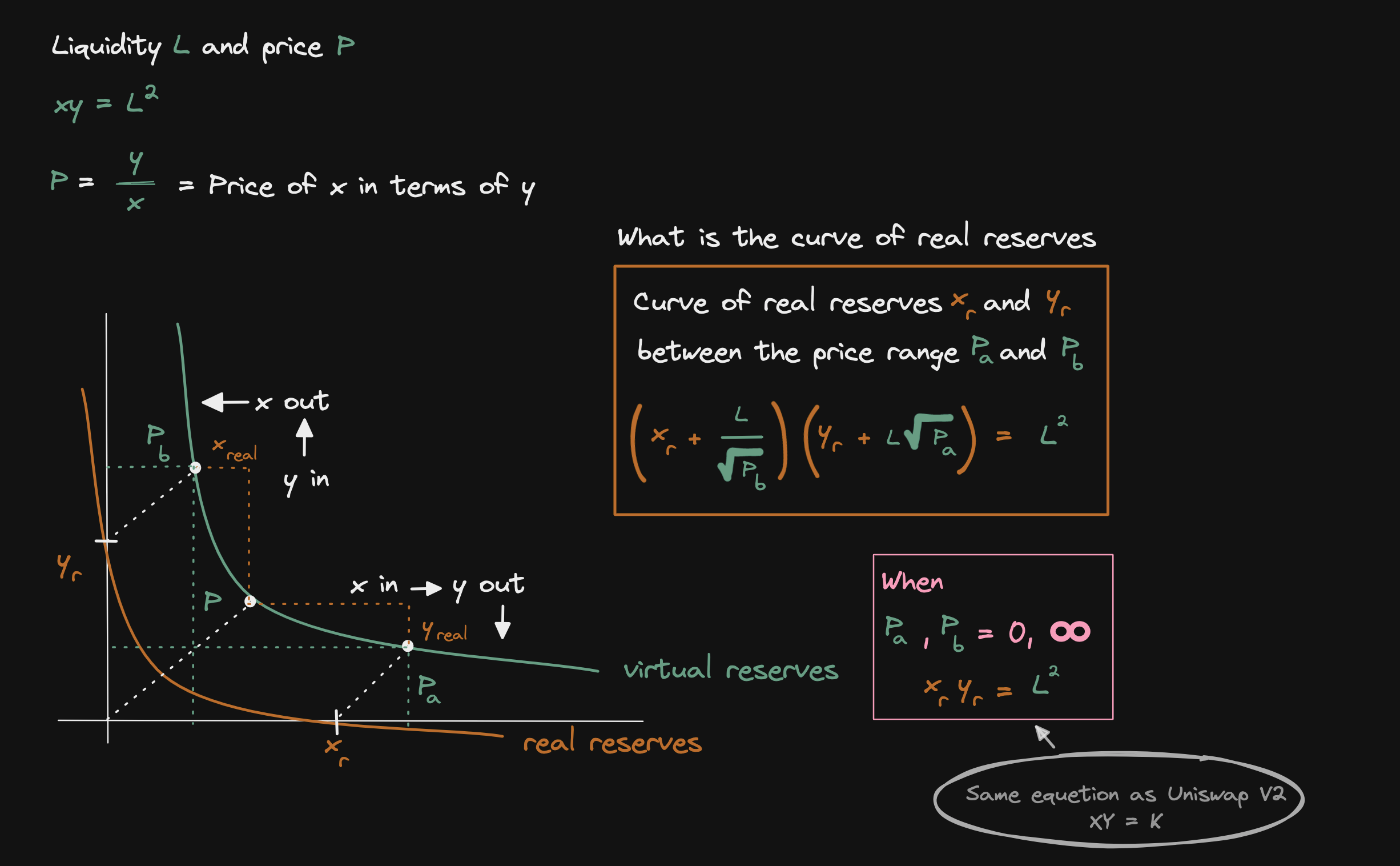
In Uniswap V3 the curve of the real reserve is giving by the formula below (orange square)

Let's derive this equation starting from the constant product equation XY = K

Maths

Let's now derive the equation, the curve for the real reserve

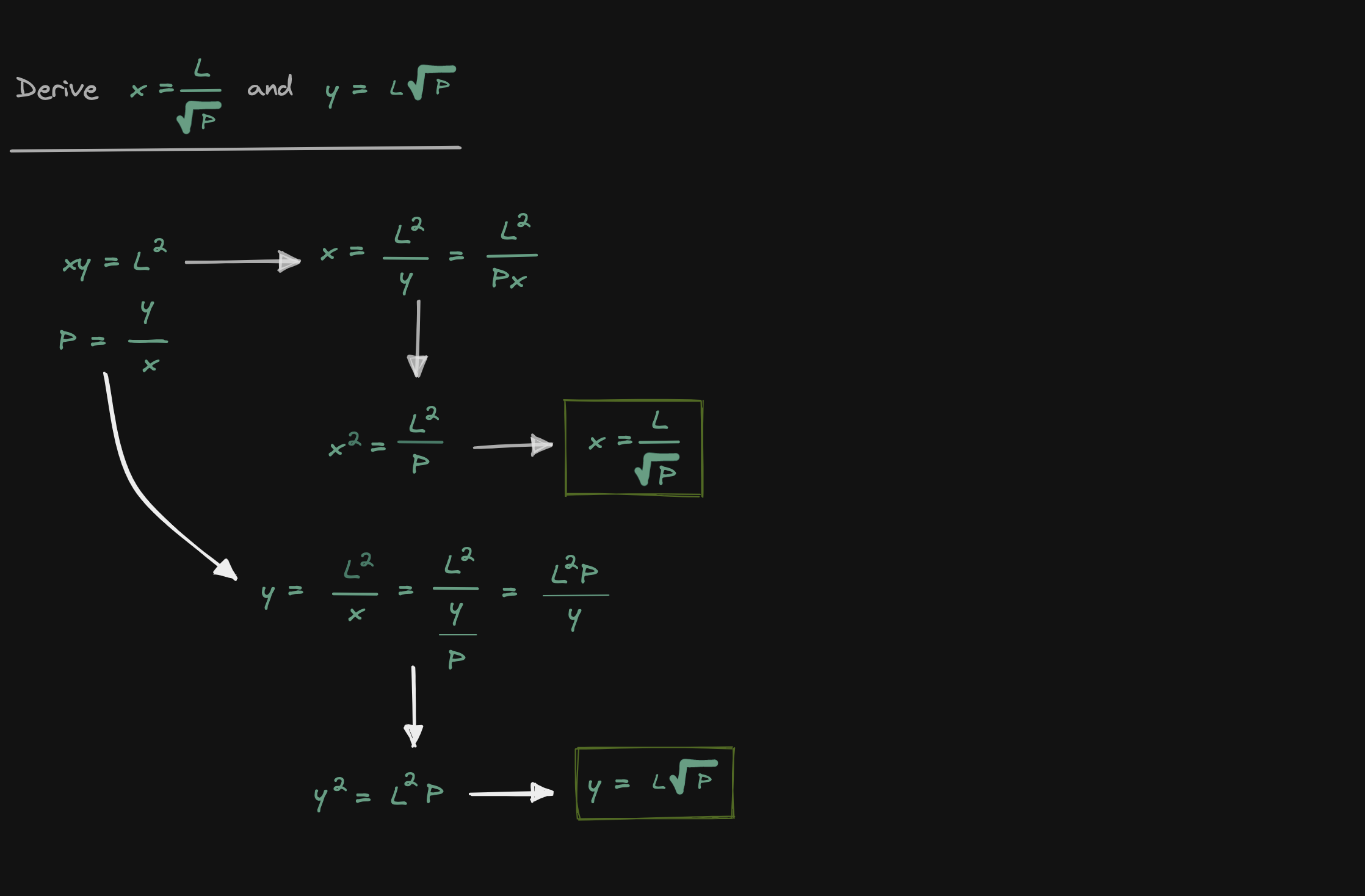
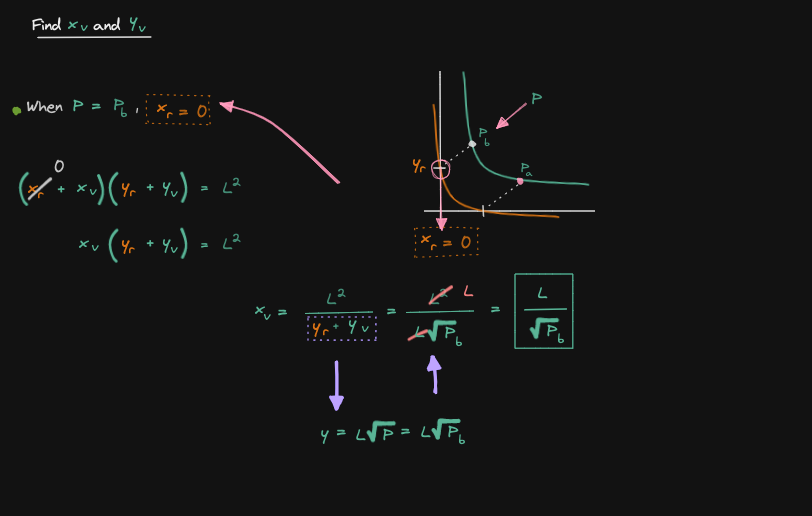
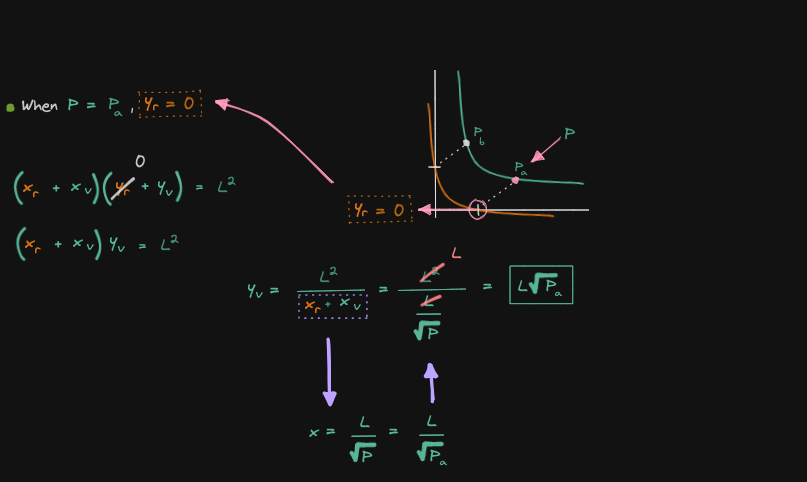
Maths

Now that we can rewrite x and y in terms of the liquidity L and the current price P, let's now derive the equation for the real reserves (solve for Xv and Yv)

Maths

Let's solve for Xv

Maths

Let's solve for Yv

Maths

The final step to derive the curve for the real reserve is to combine all of the equations that we have derived so far

Maths

Later on, we will use this equation to derive the liquidity delta: changing liquidity when we add some amount of token x and token y

(back to top)

Test Mint new position

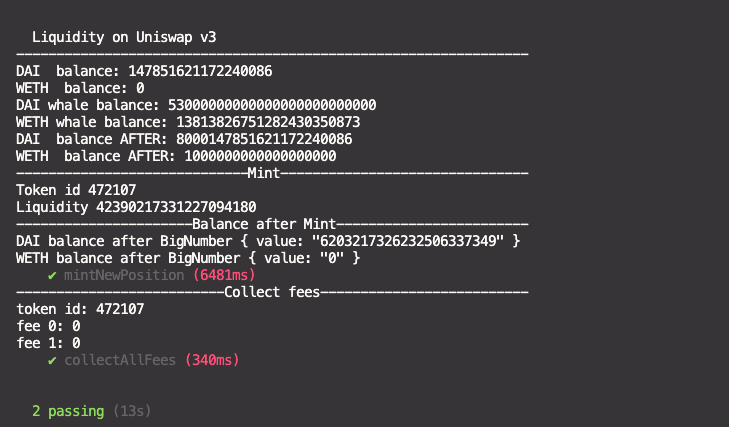
npx hardhat test test/unlock-account.test.js
npx hardhat test test/liquidityV3.test.js
Test

(back to top)

Test Collect fees

npx hardhat test test/liquidityV3.test.js
Test

No fees in this case

(back to top)

Uniswap V3 Liquidity of a single position 

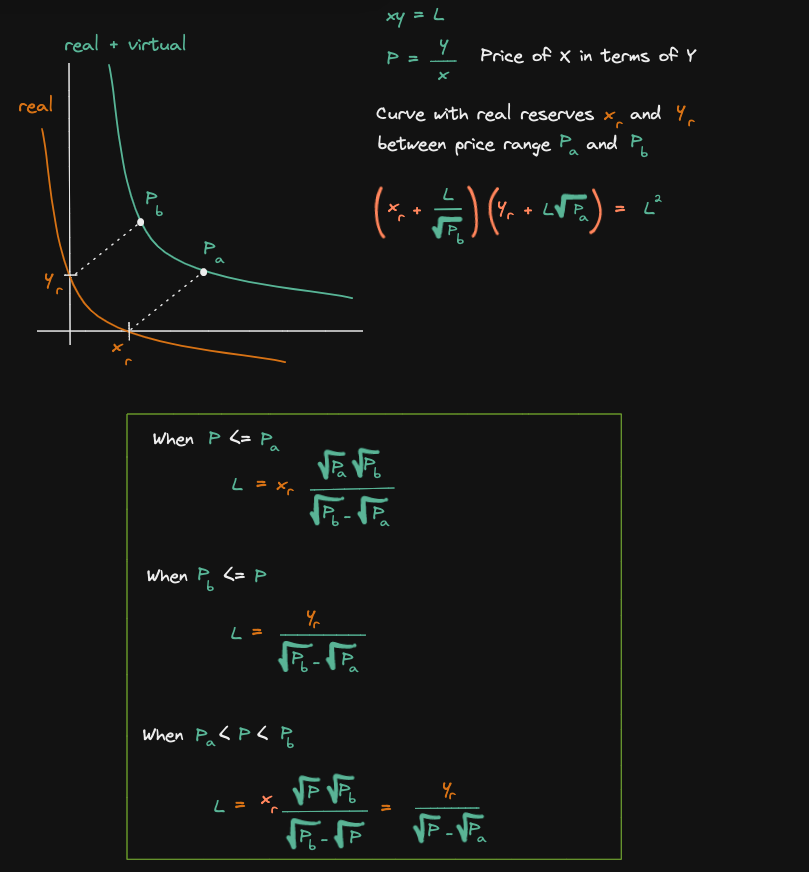
We previously derived the curve for the real reserves.

Let's use this equation to derive the equation for the liquidity(this equation has 3 parts):

Test

Let's start with the first case

Test

Let's derive the equation for liquidity when the current price >= Pb

Test

Let's apply the same technique to find Ly

Test

Find Lx and Ly

Test

Finally let's put the two equations that we derived earlier

Test

(back to top)

Test Increase liquidity

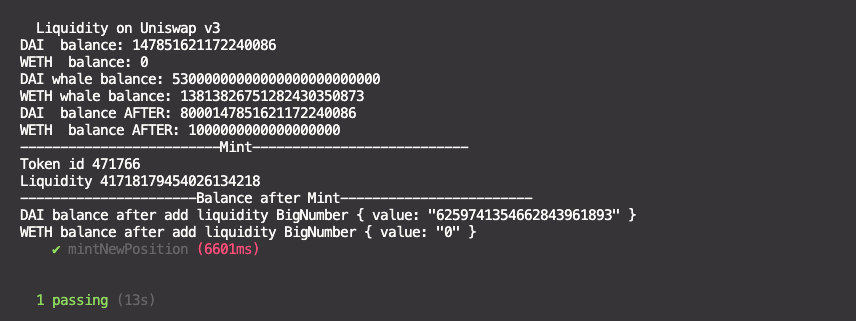
npx hardhat test test/liquidityV3.test.js
Test

(back to top)

5000 DAI and 2,77 WETH added

Amounts specified in liquidityV3.test.js:

const daiAmount = 5000n * 10n ** 18n;
const wethAmount = 10n * 10n ** 18n;

Learn more about Add liquidity - How many dx, dy to add? in this repo about Constant Product AMM

Test Decrease liquidity

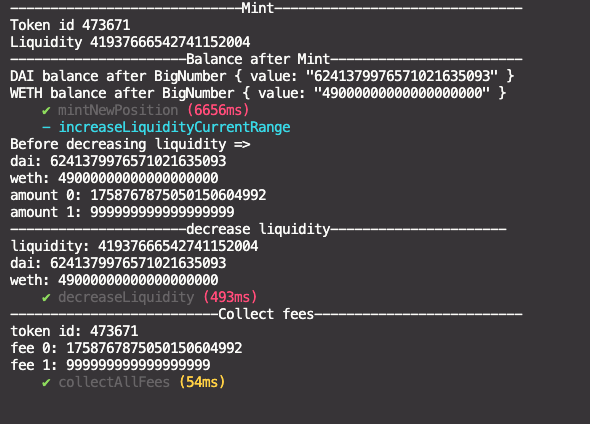
npx hardhat test test/liquidityV3.test.js

When we call the function decreaseLiquidity, it doesn't transfer the tokens back to contract

To actually withdraw the tokens from Uniswap V3, after calling the function decreaseLiquidity(), we'll have to call the function collect()

Test

Note that after calling decreaseLiquidity, DAI balance and WETH balance remain the same

(back to top)

Uniswap V3 Liquidity Delta

Test

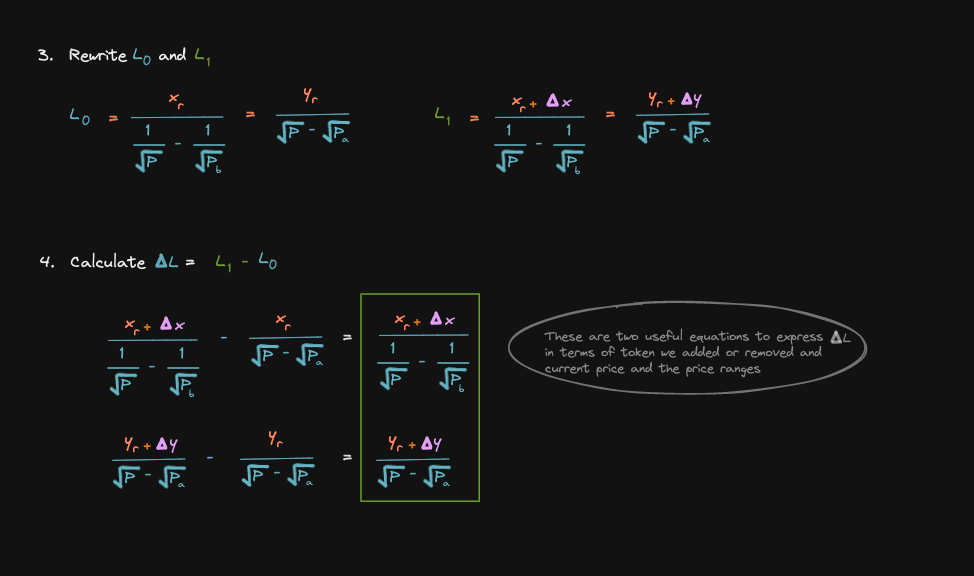
let's derive these two equations

First, preliminary math:

Test

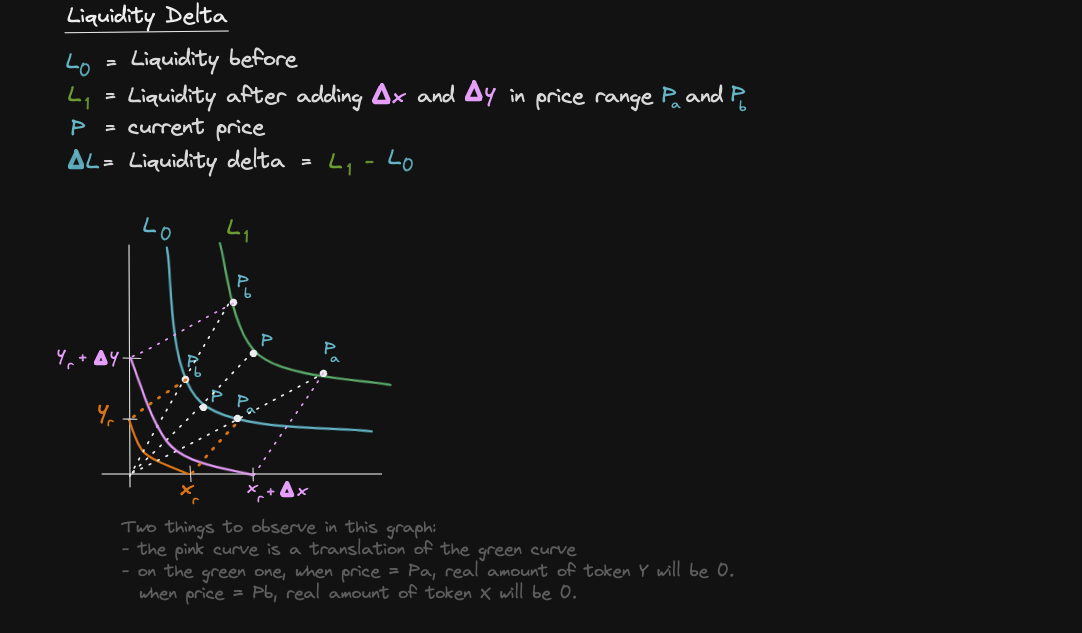
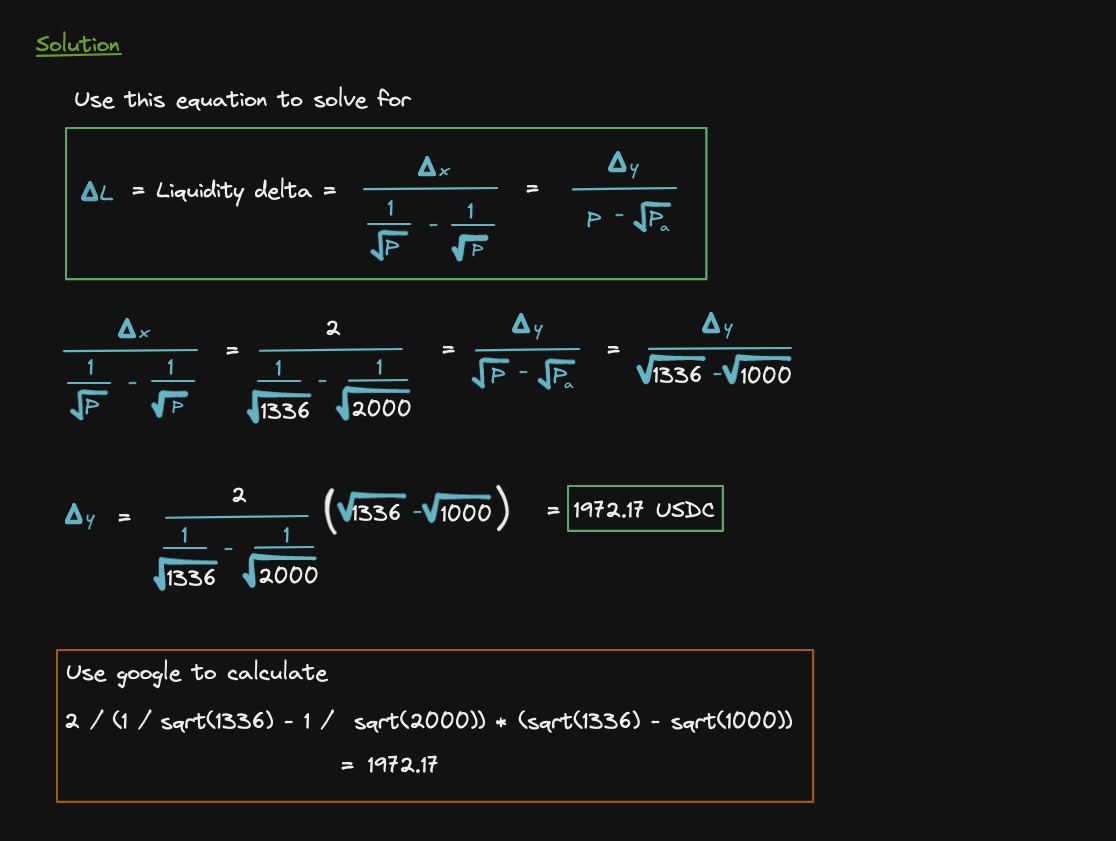
Let's define liquidity delta

Test

Four steps to calculate liquidity delta:

Test
Test

(back to top)

Uniswap V3 How many tokens to add

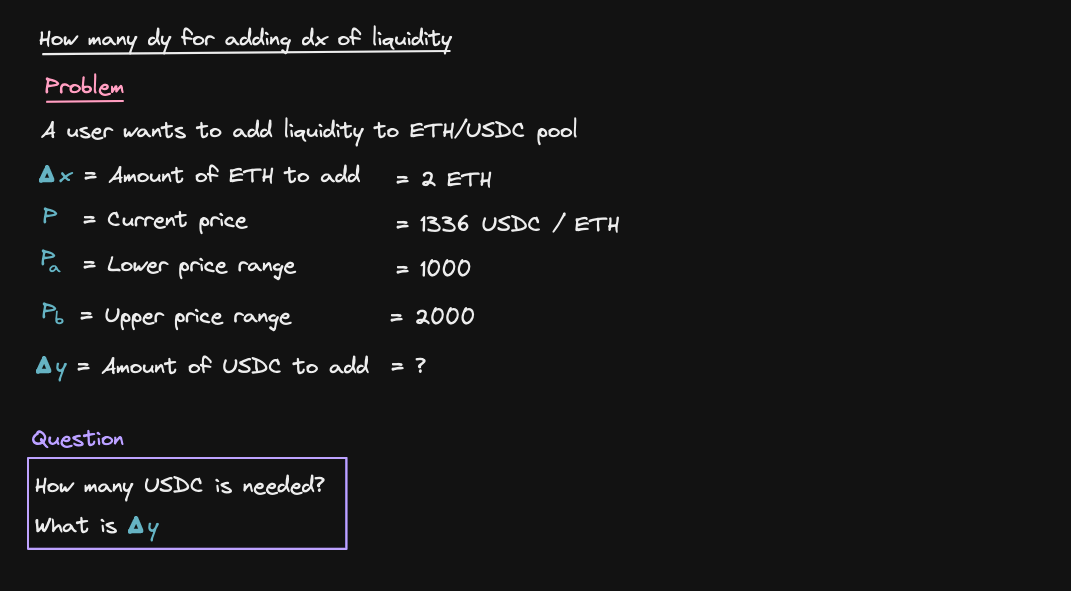
Let's see a real example of how to calculate the amount of tokens needed when we add liquidity to Uniswap V3

How much USDC will we need to add with the following parameters?

Test

How do we compute delta Y? We'll use the previous equation (Uniswap V3 Liquidity Delta)

Test

Comparing with user interface

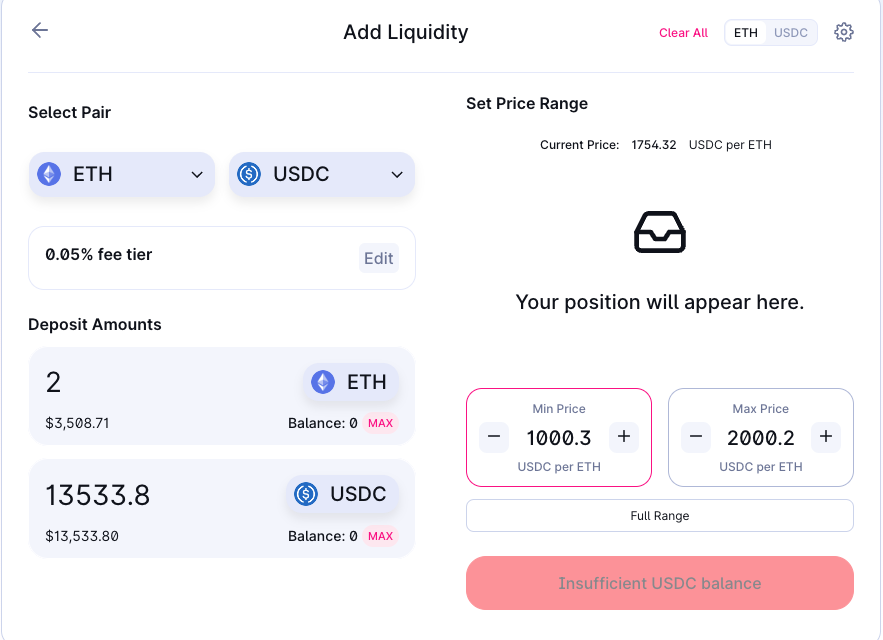
You can access the uniswap app to compare the amount of USDC that we will need to put in when the price of ETH is $1754

Test

If we compare with the UI, the result is very close

Test

(back to top)

Uniswap V3 Add and Remove Liquidity

Manage liquidity in Uniswap V3

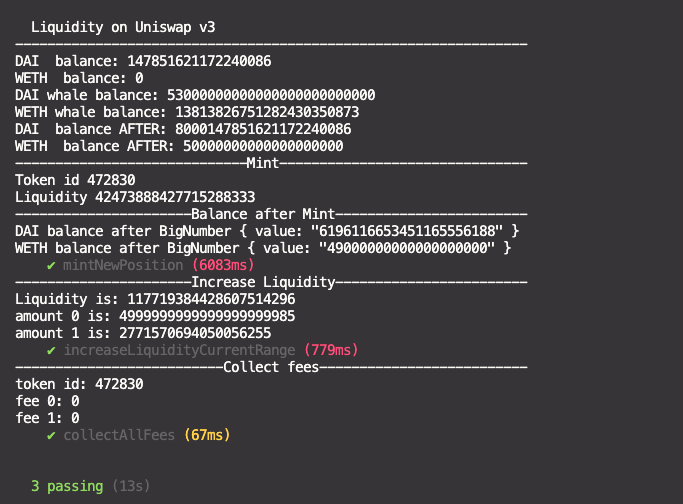
Mint new position Increase liquidity Decrease liquidity Collect fees and withdraw tokens

State variables

Contract inherits from IERC721Receiver

  1. Address of tokens. Set MIN_TICK, MAX_TICK, TICK_SPACING
  2. Set interfaces for tokens and manager with the INonfungiblePositionManager interface

Function onERC721Received

This function is called when safeTransferFrom is called on INonFungiblePositionManager.

Function onERC721Received

  1. Transfer wethAmountDesired and daiAmountDesired from msg.sender
  2. Approve amountwethAmountDesired and daiAmountDesired to router
  3. Call addLiqiuidity() on router and store wethAmount, daiAmount and liquidity returned from the function call
  4. Refund to msg.sender, excess WETH and DAI that were not added to liquidity

Function mint

This function removes liquidity from the Uniswap WETH - DAI pool.

  1. Transfer DAI and WETH from msg.sender into this contract. amount0ToAdd is DAI amount,amount1ToAdd is WETH
  2. Approve manager to spend DAI and WETH from this contract
  3. Set tickLower and tickUpper, price range to add liquidity. Both ticks must be a multiple of TICK_SPACING.
  4. Prepare parameter to add new liquidity and mint new position
  5. Add liquidity by calling manager.mint with the parameters prepared above
  6. manager.mint returns 4 outputs. Refund tokens not added to liquidity back to msg.sender. We pulled in amount0ToAdd and amount1ToAdd. Actual amount added to Uniswap V3 are amount0 and amount1.
  7. Reset approvals of DAI and WETH for manager to 0
  8. Emit Mint with tokenId.

(back to top)

Uniswap V3 Price of ETH from sqrtPriceX96

Test

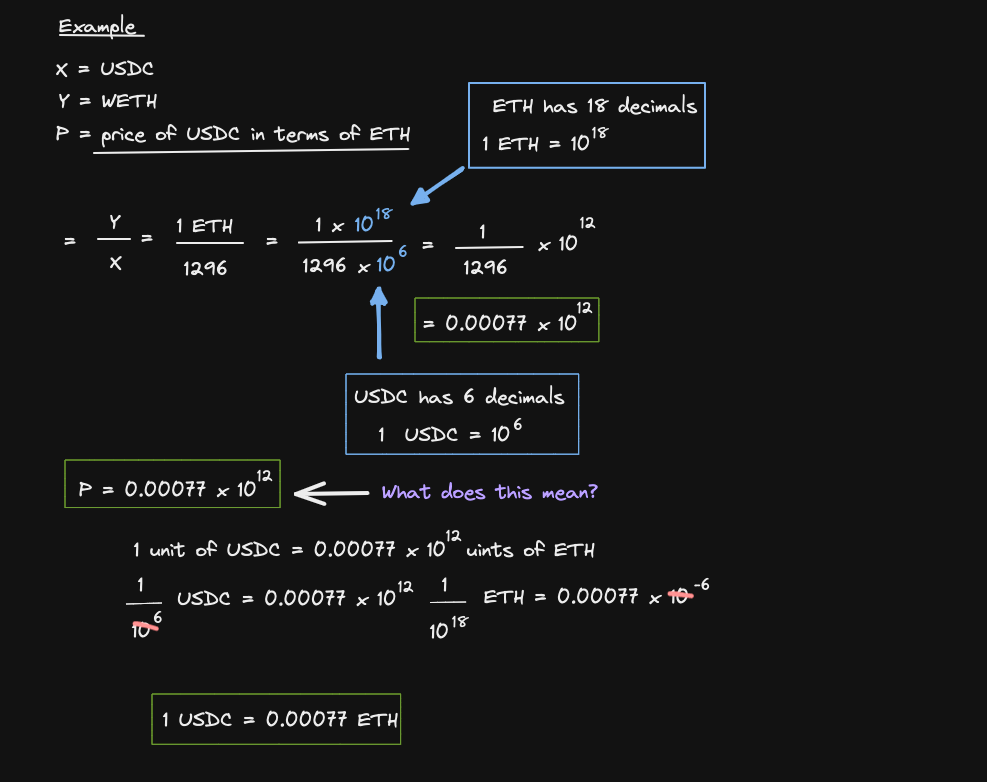
Let's find out where the 10**12 comes from

First, let's find P through an example

Test

But we are interested in the price of ETH in terms of USDC

Test

But how we calculate the price of ETH starting from sqrtPriceX96?

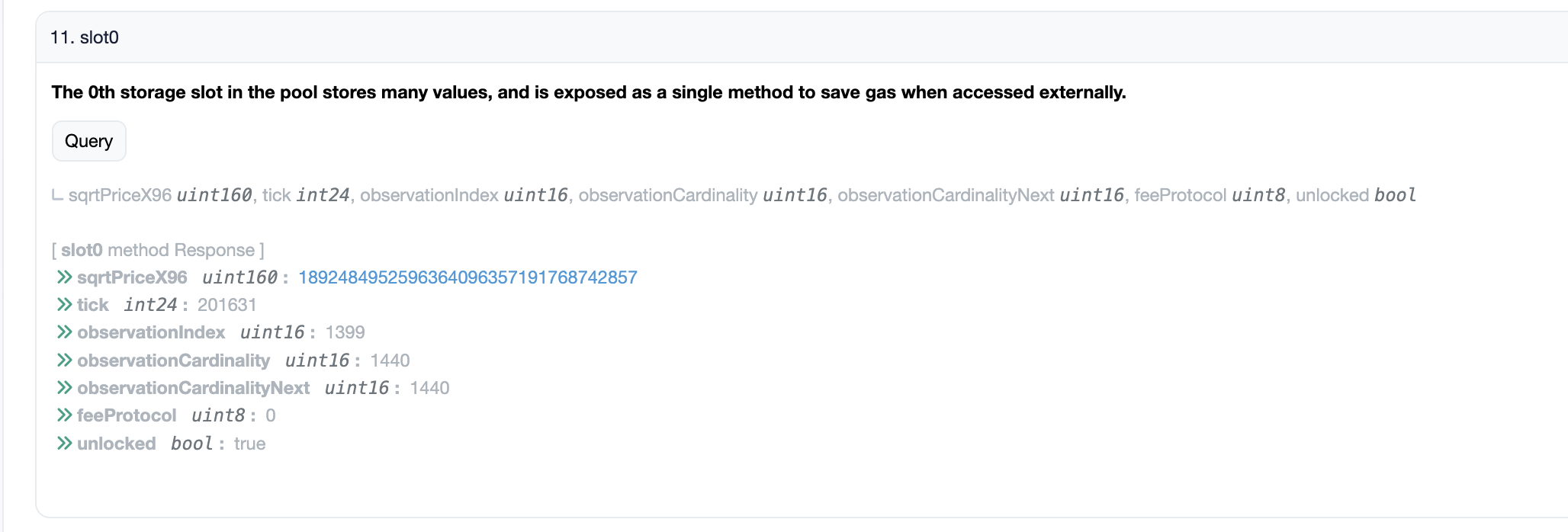
This is the variable related to the price of tokens, stored in Uniswap V3 contract

Test

Find sqrtPriceX96 variable on Uniswap USDC / ETH pool contract

Test

Let's consider sqrtPriceX96 = 2200755647817846498385002322429664. The same can be done with the actual sqrtPriceX95

Test

(back to top)

Uniswap V3 Tick and sqrtPriceX96

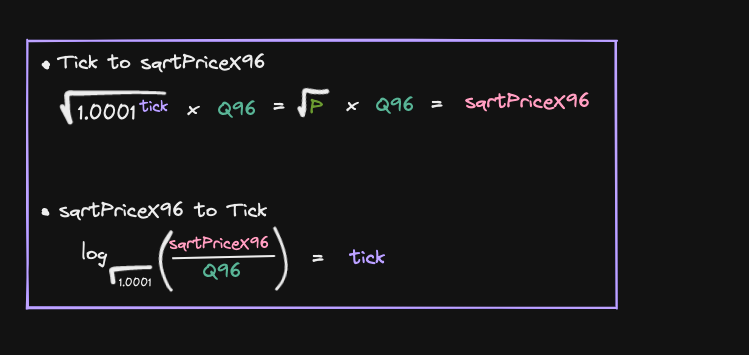
let's see how to convert from tick to sqrtPriceX96 and from sqrtPriceX96 to tick

First, let's start by reviewing some of the variables

Test

We're gonna need these two equations to calculate from tick to sqrtPriceX96 and from sqrtPriceX96 back to tick

Test

For the first example, we'll say tht we know what the tick is and we'll try to compute the sqrtPriceX96

Test

Let's use python to compute sqrtPriceX96 and tick

Use python jupyter notebook

import math

Q96 = 2 ** 96

def tick_to_sqrt_price_x_96(tick):
    return int(1.0001 ** (tick / 2) * Q96)

def sqrt_price_x_96_to_tick(sqrt_price_x_96):
    base = math.sqrt(1.0001)
    p = sqrt_price_x_96 / Q96
    return math.floor(math.log(p, base))

tick = 204632

tick_to_sqrt_price_x_96(tick)

sqrt_price_x_96 = 1892484952596364096357191768742857
sqrt_price_x_96_to_tick(sqrt_price_x_96)
Test

(back to top)

Uniswap V3 Price Change from a Swap

Test

First, let's explain what we mean by "we are assuming there is enough liquidity to swap on the curve"

Test
  • Liquidity is only supported between the price range Pa and Pb, and the price after the swap falls outside of the price range range
  • In the second case, the price P1 after the swap remains in the range Pa and Pb

Let's go over the math, let's derive the equations

Test

=> These equations can be applied to Y0, Y1, X0 and X1 since all of these points are on the curve XY = L2

This is a important fact to remember as we will derive the equations for delta x and delta y

Test

We'll do the same trick to find delta y

Test

Finally, let's derive the equations for sqrt(P1) and sqrt(P2)

Test

(back to top)

Uniswap V3 Liquidity Price Graph

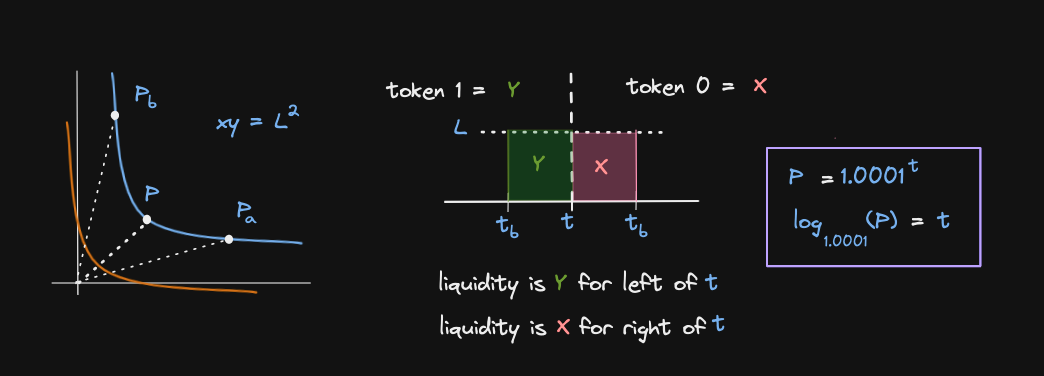
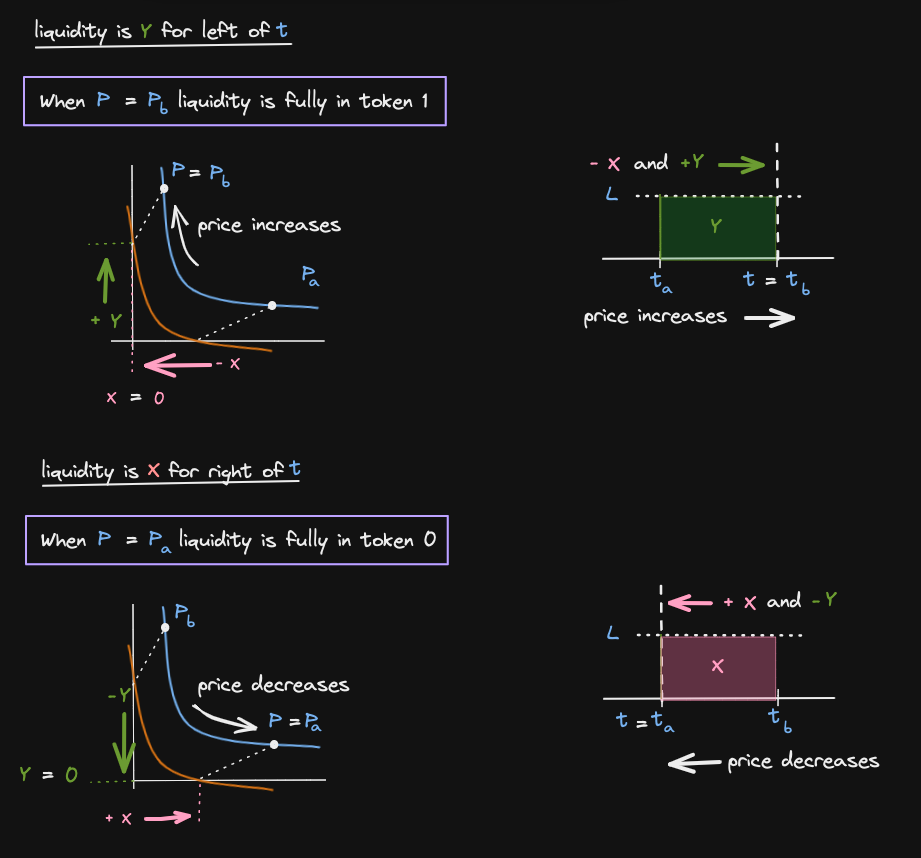
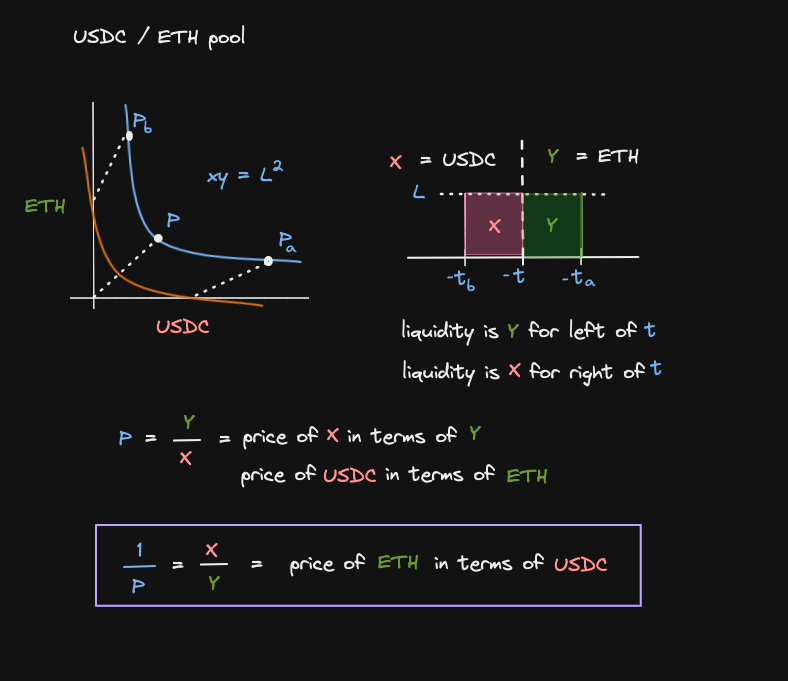
Let's see how to read liquidity price graph

The current liquidity on Uniswap v3 is L and we are trading on the curve XY = L2

There is a single position supporting this liquidity from the price range [Pa - Pb]

From Pa, Pb and the current price P, let's convert to ticks (equations inside the square) and let's map it horizontally.

The vertical axis represents liquidity

=> To the left of the current tick t, all the tokens will be in token 1 (Y)

=> To the right of the current tick t, all the tokens will be in token 0 (X)

Test

Let's see why this is:

Test

When the current price is equal to Pb, then the liquidity is fully in token Y

When the price P is equal to Pa, then the liquidity is fully in token X

=> Combinng these two observations, we know that liquidity is in Y for the left of the current tick t, and liquidity is X for the right of t

(back to top)

Uniswap V3 Liquidity Price Graph Example

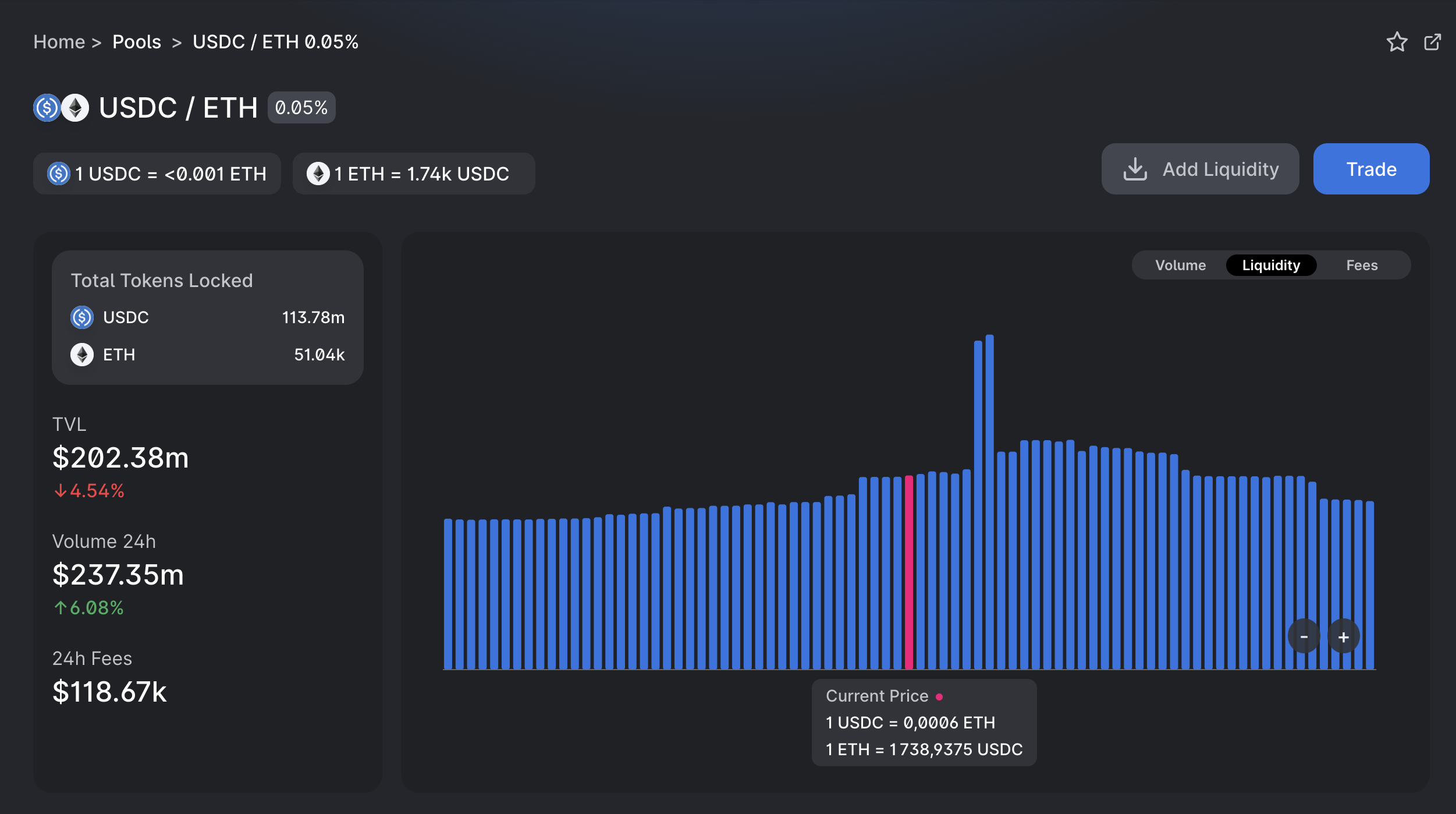
In the following Liquidity Price Graph of the ETH / USDC pool, in pink you can see the current price

To the left of the current price all of the tokens are in USDC

And to the right of the current price, all of the liquidity are in ETH

Test

Let's see why

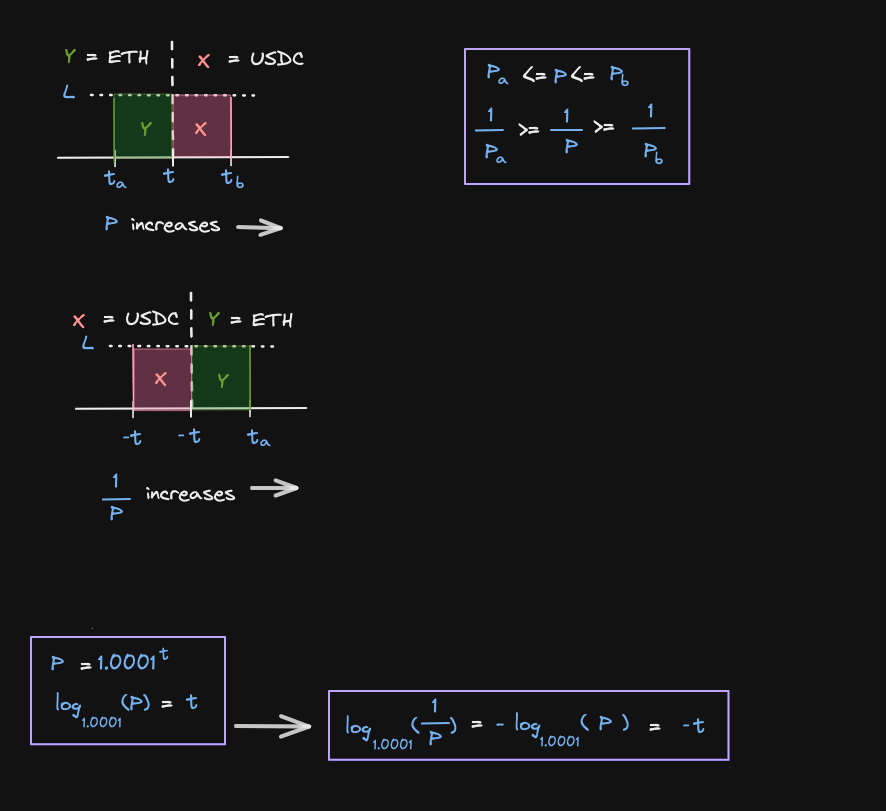
Notice that in the graph below:

  • X is on the left and Y is on the right
  • ticks are negative
Test

Instead of P increasing to the right, we want to convert this into a graph where 1 / P increases to the right

Inside the first purple rectangle below, we start by mapping the ticks to this new graph (we flip the inequality before mapping into the graph), then we convert 1 / P to ticks inside the second purple rectangle

Test

Here is the link to the ETH / USDC pool on Uniswap v3

(back to top)

Test Flash Swap

npx hardhat test test/unlock-account.test.js
npx hardhat test test/flashSwapV3.test.js
npx hardhat test test/flashSwapArbV3.test.js

Uniswap V3 Flash Swap

Borrow tokens from Uniswap V3 pool and then repay with fee in a single transaction. This is called flash loan.

We'll call flash on Uniswap V3 pool to borrow WETH.

State Variables

  1. Address of tokens and the address of the factory
  2. Set WETH interface and declare pool (IUniswapV3Pool)
  3. Set POOL_FEE to 3000 because we'll call DAI / WETH pool with 0.3% fee
  4. Declare struct FlashData with wethAmount and caller

Constructor

  1. The variable pool is immutable, so initialize it inside the constructor.
  2. Address of the pool can be obtained by calling PoolAddress.computeAddress.
  3. PoolKey can be obtained by calling PoolAddress.getPoolKey

Function flash

This function will initialize the flash loan on Uniswap V3 pool by calling pool.flash

Below is an overview of what will happen after pool.flash is called.

  • The pool sends tokens to the borrower.
  • The pool calls uniswapV3FlashCallback on the borrower.
  • Inside the uniswapV3FlashCallback our customm code is executed. At the end of the code, we must pay back the borrowed amount plus fees.
  1. Prepare data to be passed to pool.flash. Any bytes can be passed, but we will encode our custom struct FlashData.
  2. Call pool.flash
interface IUniswapV3Pool {
    function flash(
        address recipient,
        uint amount0,
        uint amount1,
        bytes calldata data
    ) external;
}

Function uniswapV3FlashCallback

This is the function called by pool, after we call pool.flash.

Here we have the requested borrow amount of WETH. Our custom code logic goes here. In this case, we will simply repay the borrowed amount plus fee.

  1. Require that msg.sender is the pool.
  2. Decode the data into FlashData
  3. Caller stored in FlashData will pay for the fee on borrow. Transfer WETH from decoded.caller into this contract for the amount fee1.
  4. Repay WETH back to the pool. Transfer borrowed amount + fee1.

(back to top)

Uniswap V3 Capital Efficiency

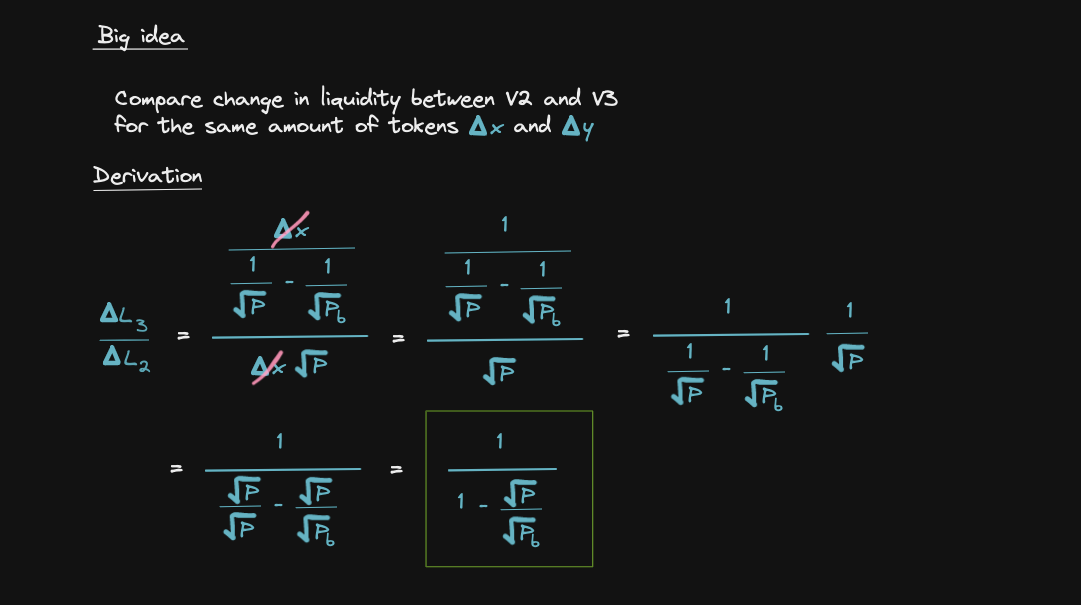
If we were to add the same amount of tokens to Uniswap v2 and Uniswap v3, then how much more can we increase the liquidity in Uniswap v3 if we were to narrow the price range?

Let's start with these equations from Liquidity Delta section to derive the capital efficiency equation

Test

As an example, we calculated the capital efficiency if we were to provide liquidity +/- 2% of the current price P

In other words, if we were to provide the same amount of token to Uniswap v2 and Uniswap v3, the amount of tokens are deltaX and deltaY

However, in Uniswap v3, let's say that we provide the liquidity for the price range +/- 2% of the current price, then the liquidity in Uniswap v3 is about 100 times greater than in Uniswap v2.

Test

We calculated the ratio of liquidity delta for Uniswap v2 and for Uniswap v3

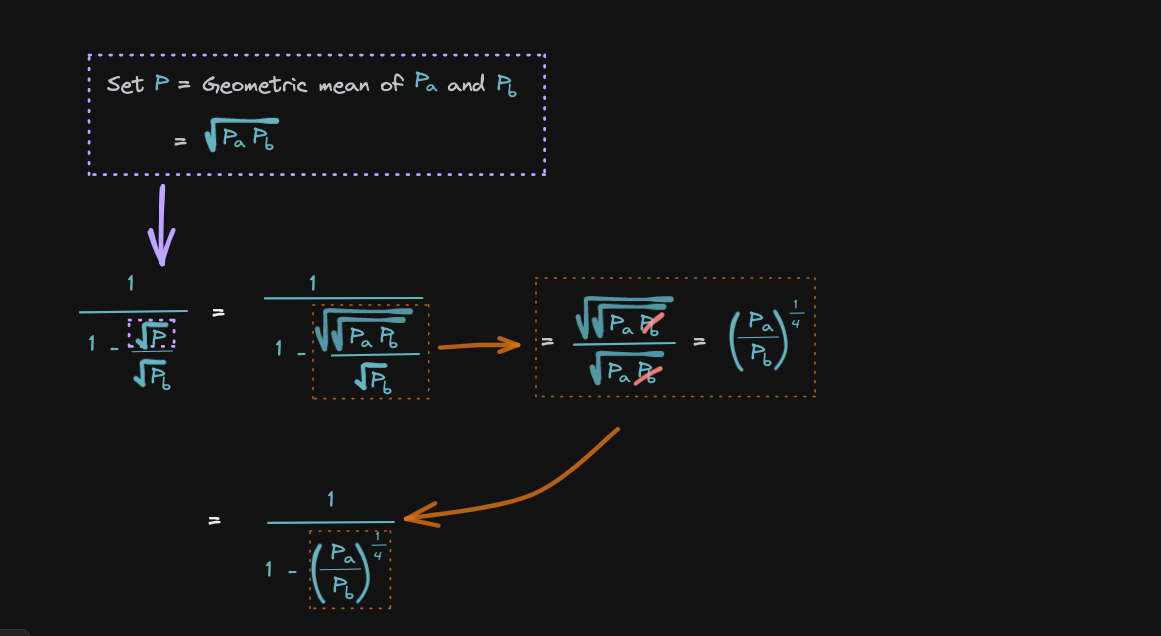
Next, let's replace the current price P with another number

  • We're going to say that the current price P is the geometric mean of Pa and Pb
  • We take the equation highlighted previously in green
  • We replace the sqrtP highlighted below by the geometric mean of Pa and Pb (sqrt(PaPb))
Test

(back to top)

Uniswap V3 Just In Time Liquidity

Alice is a liquidity provider and Bob swaps tokens.

From this trade, Alice earns some fees :)

This is how normally how a liquidity provider will earn some fees

Test

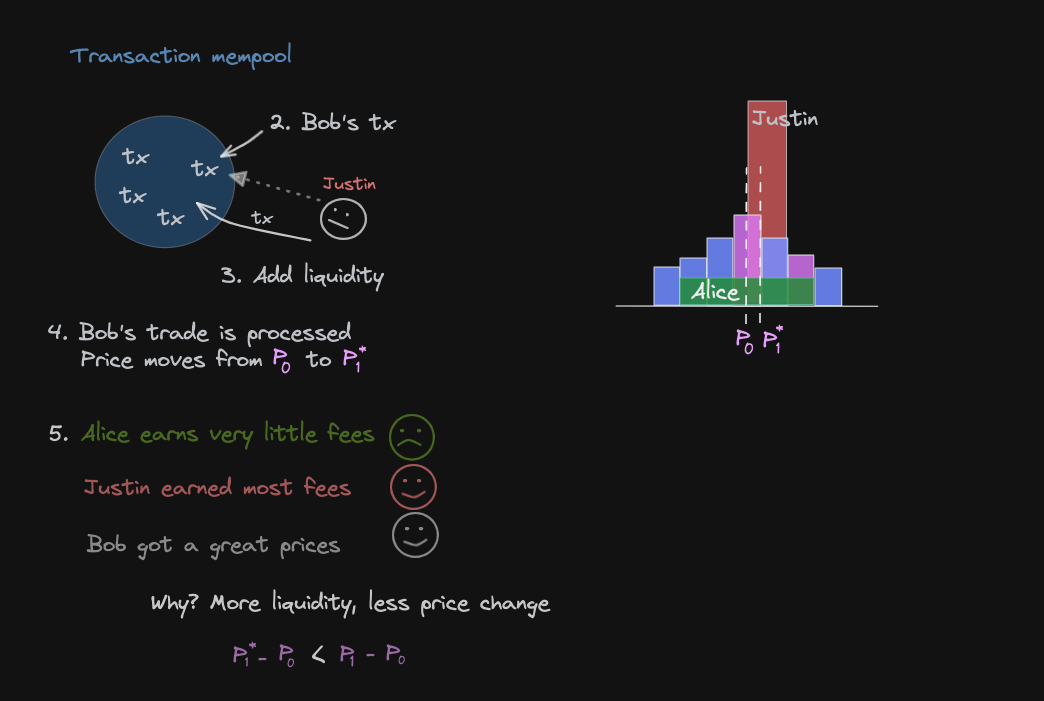
Let's see how just-in-time liquidity will change how the liquidity providers earn fees

Test

In this case, Justin sees Bob's transaction in mempool and front-runs Bob

Test

In the example above we assume that Justin has a lot of liquidity in a narrow price range including the current (shown in red)

Close to the current price P0, Aloce has provided liquidity as shown in the green area

Whereas in the same price range, Justin provided liquidity as shown in the red area, a lot more than Alice

This means that when a trade executes in this price range, Justin will earn the majority of the fees (after Bob's trade is processed)

Note that the price change from P0 to P*1 is less than the change from P0 to P1

This is beause there is a lot of liquidity arount the current price range in the second case => the price moves very little, this is called just-in-time liquidity

(back to top)

Forking mainnet

hardhat.config.js

  networks: {
        hardhat: {
          forking: {
            url: `https://eth-mainnet.alchemyapi.io/v2/${process.env.ALCHEMY_API_KEY}`,
       },
     },
  }

Note: Replace the ${} component of the URL with your personal Alchemy API key.

npx hardhat test test/swapV3.test.js

(back to top)

Note

This contract assumes that token0 and token1 both have same decimals

Consider Uniswap trading fee = 0.3%

Further reading

You can find Uniswap pools referenced below. Select a pool with the highest TVL

Uniswap V3 Pool Infos

You can find official Uniswap documentation below:

Single Hop Swap

Multi Hop Swap

Sources

(back to top)

Roadmap

  • [-] Uniswap V3 TWAP
  • [-] Further reading
  • [-] Unit test
  • [-] Flash Swap
  • Flash Swap test
  • Uniswap V3 Capital Efficiency (maths)
  • Uniswap V3 Just In Time Liquidity (maths)
  • Deploy on mainnet

See the open issues for a full list of proposed features (and known issues).

(back to top)

Contributing

Contributions are what make the open source community such an amazing place to learn, inspire, and create. Any contributions you make are greatly appreciated.

If you have a suggestion that would make this better, please fork the repo and create a pull request. You can also simply open an issue with the tag "enhancement". Don't forget to give the project a star! Thanks again!

  1. Fork the Project
  2. Create your Feature Branch (git checkout -b feature/AmazingFeature)
  3. Commit your Changes (git commit -m 'Add some AmazingFeature')
  4. Push to the Branch (git push origin feature/AmazingFeature)
  5. Open a Pull Request

(back to top)

License

Distributed under the MIT License. See LICENSE.txt for more information.

(back to top)

Contact

Reda Aboutika - @twitter - reda.aboutika@gmail.com

Project Link: https://github.com/Aboudoc/Uniswap-v3.git

(back to top)

Acknowledgments

(back to top)