Modulation Schemes

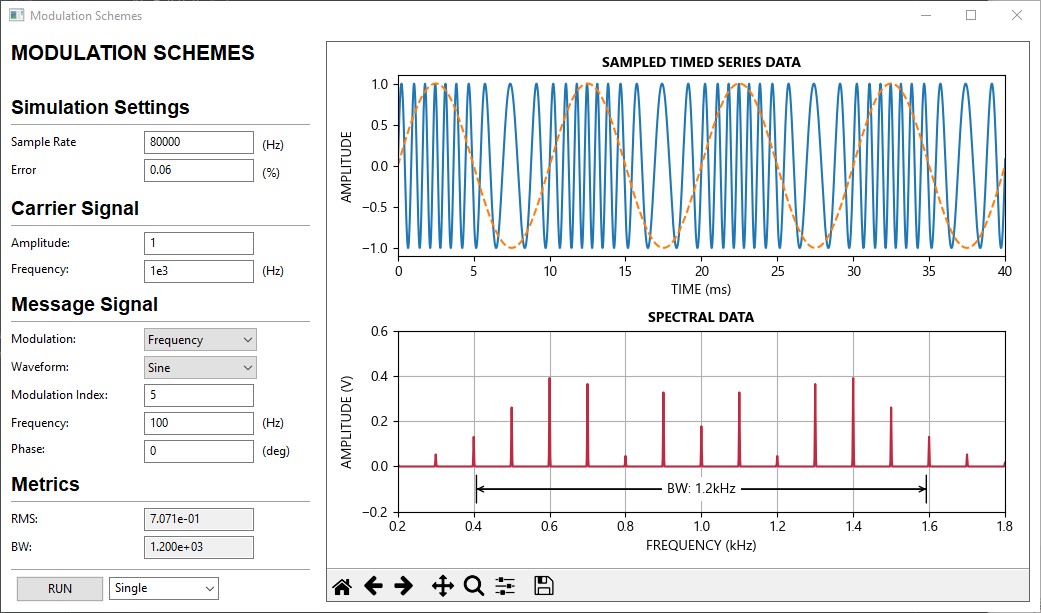
This application demonstrates various modulation schemes.

The Signals

$\text{carrier signal: }c(t)%20=%20A_c%20cos%20(2%20\pi f_c t)$

$\text{message signal: }m(t)%20=%20A_m%20cos%20(2%20\pi%20f_m%20t%20+%20\varphi_m)$

Amplitude Modulation

$s(t) = c(t) \times m(t)$

Phase Modulation

$s(t) = cos (2 \pi f_c + k_p m(t))$

$BW=2f_m\left(\beta+1\right))$

Bandwidth for shift keyed signals

$BW_{keying}=f_c + f_m - (f_c - f_m)$

Frequency Modulation

$s(t)=A_c \cos\left(2 \pi f_ct + 2\pi k_f \int_{0}^{t}{m\left(\tau\right)d\tau}\right)$

Let's understand why...

For a given frequency modulated signal, the frequency is directly proportional to the magnitude of the modulating message such that any change in modulation has a linear effect on the resulting signal frequency. To show this, the instantaneous frequency is expressed as:

In musical terms, the instaneous frequency is merely the representation of tones we hear. The pitch of one's voice, for instance, or the note of a tuning fork. As the number of these tones we hear increase, so does the complexity of our equation describing the instantaneous frequency. In other words, the instantaneous frequency describes the mish-mash of frequencies captured by your ears, or say a measurement.

In the field of photonics, lasers are used to create and transmit mono-tone (single-frequency) signals. In more complex cases that are more common, multimode lasers are also used, which require a bit more finesse in identifying the multiple frequencies and their various amplitudes composing the signal. In pulsed or chirped optical signal generators, instantaneous frequency can vary with time. That is, a frequency modulation.

Let's suppose for a moment the modulating signal was zero. The instantaneous frequency would be expressed solely by the carrier frequency:

To express a sinusoidal waveform at this frequency, we must first compute the angular frequency from the above expression. Normally, this is simply:

$\varphi_{i}(t) = 2\pi f_c$

However, what really has happened is we have unconsciously computed the instantaneous phase (which is expressed in radians).

While instantaneous phase (and conversely instantaneous frequency) are not generally covered, the understanding of phase or frequency modulation requires explicit definition of these terms. As we explore these definitions further, our familiar understanding of trigonometric operation will also benefit from this imbued clarity. So, to understand instantaneous phase more, we first begin by defining a generalized expression:

$\varphi_i(t) \equiv 2 \pi \int_0^t{f_i(\tau) d\tau}$

We compute the integral of our instantaneous frequency to arrive at our instantaneous phase, which is merely the sum of our frequency term over a period of time, in this case, t, and then mapped to the unit circle, which has a circumference of 2π.

Since our frequency is constant (scalar), the result is straightforward:

$\varphi_i(t) \equiv 2 \pi \int_0^t{f_i(\tau) d\tau}$

Recall that our frequency has units of inverse time equal to the period of one traversal around the unit circle in seconds. Now, note the t term in the above expression. Let's rewrite the expression:

$\varphi_i(t) \equiv 2 \pi \int_0^t{f_i(\tau) d\tau}$

What has happened is we have defined a ratio which marks our traversal around the unit circle in increments of phase. So when t=0, our instantaneous phase is 0. When our watches have progressed to 50% of our period, our instantaneous phase is π (or 180°) or half the unit circle.

Sinusoidal functions, such as cosine and sine, are trigonometric functions which only accept arguments of instantaneous phase because it marks where along the unit circle they currently are. Much like a clock on the wall, to know our time, we must know the position of the clock hands.

So when the frequency of FM signals is defined as the linear change with respect to the modulated amplitude - that is,

we must compute the instantaneous phase first before we can make any use of trigonometric functions. Again, this is because trigonometric functions accept only arguments of angular frequency, aka the instantaneous phase marking where along the the unit circle they are.

Compute the instantaneous phase of the general expression

$\varphi_{i}\left(t\right)=2\pi\int_{0}^{t}{f_i\left(\tau\right)}d\tau=2\pi\left(f_ct+k_f\int_{0}^{t}m\left(\tau\right)d\tau\right)$

Which defines the trigonometric argument for the frequency modulated waveform:

$s(t) = A_c cos ( s(t)=A_c \cos\left(\varphi_{i}\left(t\right)\right)$

$s(t)=A_c \cos\left(2 \pi f_ct + 2\pi k_f \int_{0}^{t}{m\left(\tau\right)d\tau}\right)$

$\text{modulating index: }\beta=\frac{\Delta f}{f_m}=\frac{k_fA_m}{f_m}$

$\boxed{BW=2f_m\left(\beta+1\right)}=2(\Delta f+f_m)$

Bandwidth for shift keyed signals

$BW_{keying}=2f_m\left(\frac{1}{T}+\beta f_m\right)+f_m$

Integration

Cosine

$m\left(t\right)=A_m\cos{\left(2\pi f_mt+\varphi_m\right)}$

$M\left(t\right)=\frac{A_m}{\pi f_m}\sin{\left(\pi f_mt\right)}\cos{\left(\pi f_mt+\varphi_m\right)}$

Sine

$m\left(t\right)=A_m\sin{\left(2\pi f_mt+\varphi_m\right)}$

$M\left(t\right)=\frac{A_m}{\pi f_m}\sin{\left(\pi f_mt\right)}\sin{\left(\pi f_mt+\varphi_m\right)}$

Note: scaling to the appropriate time-base is required. If evaluating across N, divide M[n] by the sampling frequency.

Triangle

$T = \text{period length}$

$m\left(t\right)=\frac{2}{\pi}\sin^{-1}{\left[\sin{\left(\pi t\right)}\right]}$

$m\left(t\right)=\frac{4}{T}\left|\left(\left(t-\frac{T}{4}\right)\ \mod\ T\right)-\frac{T}{2}\right|-1$

$m(t) = \left{\begin{matrix}\frac{4}{T}t - 1 & t<T/2\\ -\frac{4}{T}t^2 + 3 & t\geq T/2\end{matrix}\right.$

$M(t) = \int_{0}^{t}{m\left(\tau\right) d\tau} = \left{\begin{matrix}\frac{2}{T}t^2 - t & t<T/2\\ -\frac{2}{T}t^2 + 3t & t\geq T/2\end{matrix}\right.$

Note: scaling to the appropriate time-base is required. If evaluating across N, divide M[n] by the sampling frequency.

Sawtooth

$t = x \mod T$

$m\left(t\right)=\frac{t}{T} =\frac{x \mod T}{T}$

$M\left(t\right)=\int_{0}^{t}m\left(\tau\right)d\tau=\int_{0}^{t}{\frac{\tau}{T}d\tau}=\boxed{\frac{1}{T}\left(x \mod T\right)^2-\left(x \mod T\right)}$

Note: scaling to the appropriate time-base is required. If evaluating across N, divide M[n] by the sampling frequency.

Square

$m(t)=\begin{cases}1 & \text{ if } t<T/2 \ -1 & \text{ if } t \geq T/2 \end{cases}$

$M(t)=\int_{0}^{t}{m(\tau)d\tau}=\begin{cases} t & \text{ if } t<T/2 \ -t & \text{ if } x \geq T/2 \end{cases}$

Note: scaling to the appropriate time-base is required. If evaluating across N, divide M[n] by the sampling frequency.

Shift Keying

import numpy as np

fs = 100000 # sampling frequency
fm = 100    # modulating frequency
T = fs/fm   # samples per period

# repeat
mt = np.repeat(binary_message, T)[:N]

# or ravel
mt_ = np.ravel(np.matlib.repmat(binary_message, T, 1), order='F')[:N]

# or kronecher
array_ones = np.ones(T)
mt__ = np.kron(binary_message, array_ones)[:N]

# integral
Mt = x * (2 * m(t) - 1)

Note: scaling to the appropriate time-base is required. If evaluating across N, divide M[n] by the sampling frequency.

Example: The number of samples contained in the buffer of your measurement window. In other words, the number of samples collected is defined by:

N = 7

The number of samples contained in one period of the modulating frequency

T = fs/fm = 2

The message being transmitted

binary_message = [1, 0, 1, 1]

Message is repeated T number of times

mt = [1, 1, 0, 0, 1, 1, 1, 1]

Depending on the number of samples available in the measurement buffer, m(t) may become truncated:

mt = m(t)[:N] = 1, 1, 0, 0, 1, 1, 1]

If modulation scheme is Phase shift-keying (PSK):

pi = np.pi
mt = pi * m(t) = [pi, pi, 0, 0, pi, pi, pi]

Tektronica/modulation_schemes

Modulation Schemes

The Signals

Amplitude Modulation

Phase Modulation

Frequency Modulation

Integration

Cosine

Sine

Triangle

Sawtooth

Square

Shift Keying