/diffusion-model-learning

A time singal diffusion model implement shared by wzy

Primary LanguagePython

如何手搓扩散模型

趁着SORA的话题性，我把一年前写的扩散模型原理整理出来，希望能对之后的工作有帮助。 扩散模型是近年来比较热门的神经网络模型，我认为所谓扩散模型就是对扩散过程进行数学建模，并且能够逆转扩散过程的数学方法。 本文将开始从一个初学者的视角尝试理解它的**和应用。 另外，提供了两个例子，说明极其简单的扩散模型就可以实现一维信号甚至图像的“生成”。 最后，对扩散模型背后的数学原理进行了简要推导，以备后用。

本文相关代码整合在这些以下开源地址

何为扩散模型

所谓扩散就是布朗运动，体现在数学概念上，我们可以将它理解成数据样本点的分布向标准正态分布不断靠拢的过程。这个过程如下图所示，左图中的曲线代表一组高维数据，它拥有连续维度，不同维度的采样值曲线上蓝色点所示，它们的分布如右侧红色点所示。而经过“扩散”之后，采样值的分布逐渐符合标准正态分布，如右图所示。

所谓扩散模型就是对上述扩散过程进行数学建模，并且能够逆转扩散过程的数学方法。我觉得这方面介绍得比较清楚的论文是以下这篇，虽然题目中没有扩散的字眼，但“非平衡的热动力学”这个名词非常写意，甚至有些浪漫。

Deep Unsupervised Learning using Nonequilibrium Thermodynamics

热力学定律告诫我们，扩散无法避免、熵增无法避免，也就是说宇宙总是向着更加混乱和无序发展的，而维持有序则需要外界不断对某个系统施加能量。那么这个无序的状态可以看作是变量服从正态分布，而有序的低熵状态则代表上述的曲线。它上面的采样值服从未知但确定的分布。

从例子中可以想见，一条有序的曲线经过若干次简单的计算后即可“退回”到正态分布的混沌状态，且这个过程是连续的，或局部可微的。因此，我们同样有理由相信这个过程是“可逆的”，只需要“学会”每一步扩散的微分步骤，就可以在数学上把这个物理上难以维持的过程给反转过来。

为了这个目标所做的一切努力，就是扩散模型，它的优势有四点：（深度网络）模型结构不限、能够实现采样、易与其他概率密度结合、易与样本状态结合。

  1. extreme flexibility in model structure,
  2. exact sampling,
  3. easy multiplication with other distributions, e.g. in order to compute a posterior,
  4. the model log likelihood, and the probability of individual states, to be cheaply evaluated.

扩散过程的简要原理

为了表达方便，我们将采样值（曲线）的分布表示为

$$ x_0 \sim \Psi(x) $$

它代表一个确定但未知的分布。而我们认为经过一段时间的随机扩散后，新分布属于正态分布

$$ x_T \sim \mathcal{N}(\mu, \Sigma) $$

为了简单起见，通常假设它服从标准正态分布

$$ \begin{cases} \mu = 0 \\ \Sigma = I \end{cases} $$

因此，扩散过程可以表示成变量连续变化的过程

$$ x_0, x_1, x_2, ..., x_T $$

直觉上来讲，它可以是一条 Markov 链，其转移概率为

$$ p(x_t) = p(x_{t-1}) \cdot p(x_t|x_{t-1}) $$

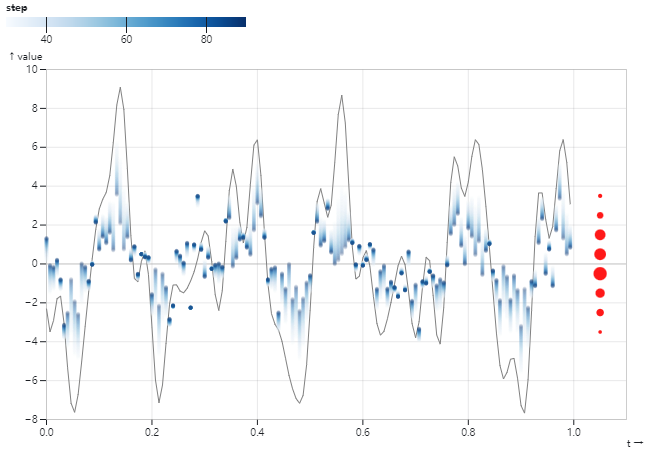
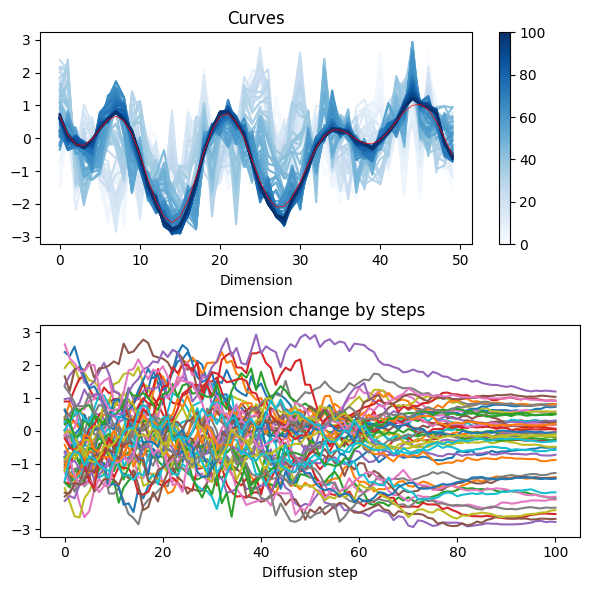
连续变化过程如下图所示，虽然它是一张静态图，但我希望通过轨迹模糊使它看上去有一些动态的感觉。

Untitled

扩散模型对信号的理解

前文说到扩散模型是尝试逆转扩散过程的数学方法，那么立即产生的问题就是如何对“扩散”进行可计算的描述。本文尝试从两个角度解读我们日常观测到的信号，相信它们不仅有助于理解随机变量，也有助于后续引入扩散的计算方法。在扩散模型中，我更加倾向于将红线理解成对均值为零的随机变量进行的一次采样，它背后的逻辑是“随机性先于一切而存在，而我们观测到的信号只是对某个高维的随机变量进行了一次采样”。

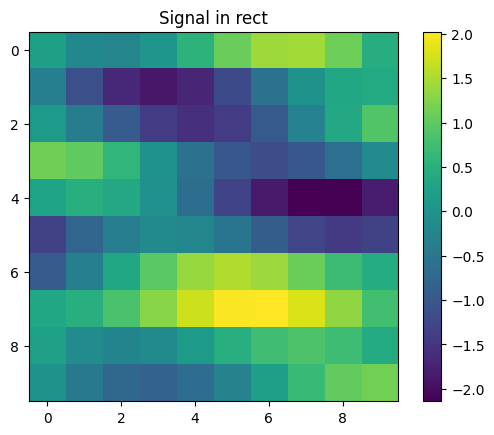
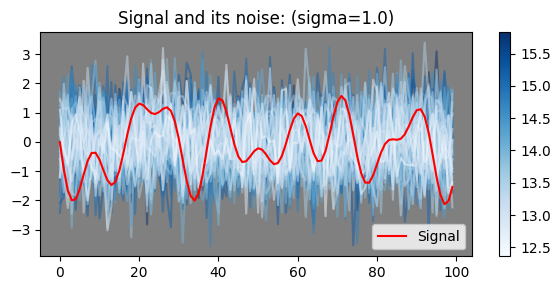
信号是某个客观事物的直观表达，我们可以用高维向量的观点去理解它。假设我们对一个连续的函数进行采样，那么每个采样值就是它的维度。下图是一个例子，左侧是一张 $10 \times 10$ 的图（虽然它没能实际意义），右侧中红线是图中的每个像素转换成一条向量 $\hat{x}$，而它背后的蓝白色曲线就是它加上一些噪声的例子，为了方便起见，我们将它们统称为“信号”，该信号也是 $100$ 维的向量。

Untitled

Untitled

接下来，我们关注蓝色曲线，这是典型的“确定值加噪声的形式”，它们满足正态分布

$$ \begin{cases} X \sim \mathcal{N}(\mu, \Sigma)\\ \mu = \hat{x}\\ \Sigma = I \end{cases} $$

易知，每条蓝色曲线出现的概率为

$$ p(x) = \mathcal{N}(x; \mu, \Sigma) $$

下面我们开始考虑一个问题，那就是红色的线是什么？这个问题十分重要，因为我们如何理解它，决定了我们如何对它进行扩散和建立对应的扩散模型。我现在有两种理解方式，一是将红线理解成方差为零的随机变量，二是将红线理解成对均值为零的随机变量进行的一次采样。

信号是方差为零的随机变量

将红线理解成方差为零的随机变量是非常直观的想法，它背后的逻辑是

信号先于随机性而存在，以均值的形式存在，而观测这个信号得到的值是均值与噪声相加得到的采样值。

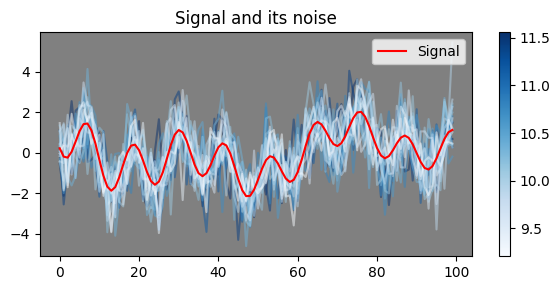
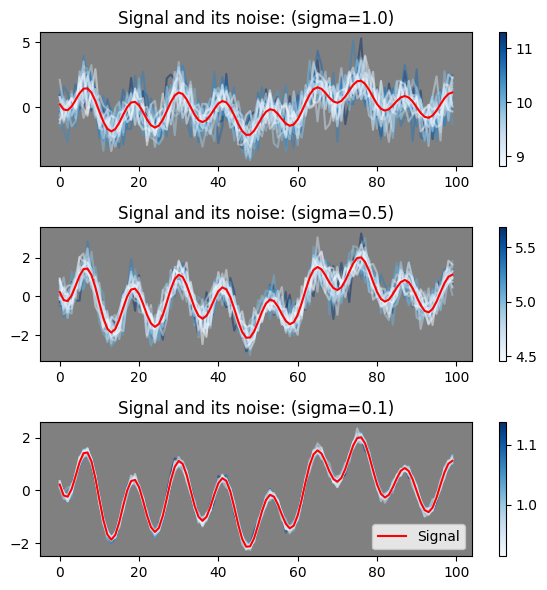
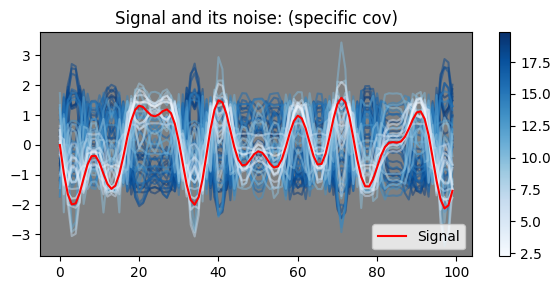
这个过程如下图所示，随着噪声方差越来越小，信号的“不确定性”也越来越小，直到减少到零时得到完全确定的信号。右侧的 colorbar 代表该颜色的采样值曲线与红线之间的欧氏距离。这种**无疑是有效的，但其有效性不会突破它的适用范围，也就是说它适用于解决那些“信号先于随机性存在的问题”，只要我们能够把方差降下来，那么感兴趣的信号就会自然浮现出来。比如通过多次取平均的方式减少系统误差的方法就是典型应用之一

$$ \begin{cases} \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X \\ Var(\frac{X}{n}) = \frac{Var(X)}{n^2} \end{cases} $$

$$ Var(\bar{X}) = \frac{Var(X)}{n} \rightarrow \lim_{n \rightarrow \infty} Var(\bar{X}) = 0 $$

Untitled

信号是随机变量的一次采样

另一个观点是将红线理解成对均值为零的随机变量进行的一次采样，它背后的逻辑是

随机性先于一切而存在，而我们观测到的信号只是对某个高维的随机变量进行了一次采样。

当然，这里我们需要进一步分析这个高维空间长什么样子，以及如何从概率密度的角度研究我们为什么能够，或者说已经观察到这组采样结果。

从协方差的角度理解扩散模型

我在前文抛出一个概念，那就是随机性先于一切而存在，而我们观测到的信号只是对某个高维的随机变量进行了一次采样。本文尝试从协方差矩阵的角度来说明有意义的信号处于更低秩的状态，说明其背后的逻辑更加简单。从这个观点来看，噪声比信号更加复杂，那么我们用复杂的噪声去表达简单的信号，这个思路应该是可行的。

基本假设

下图表示我们不再认为观测到的信号是噪声与“原始信号”的叠加（见左侧），而是认为观测信号是某个分布的采样（见右侧）。如果我们只讨论可能性的话，只要噪声信号的方差足够大，它总有希望“生成”有意义的信号，我们只需要碰巧把它采样出来。

但这个假设显然不够有说服力，因为我们很难想象能够从高维度的，且各个维度服从独立同分布的高斯分布中“采样”到任何有意义的信号。这个做法像是在键盘上洒把米，然后让鸡啄出科研论文一样荒谬。

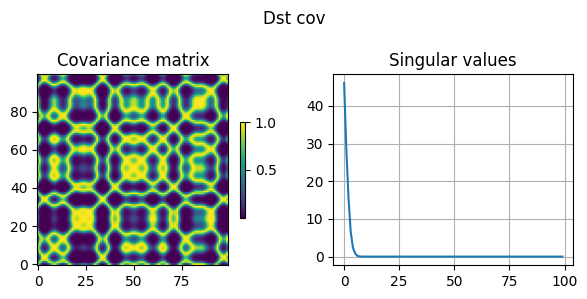
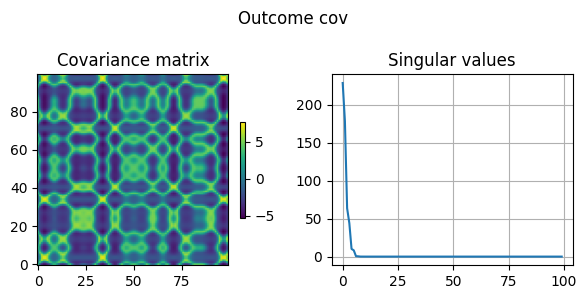
Untitled

从协方差矩阵看简单与复杂

有意义的信号具有连续性和复杂性，如果我们对它的协方差矩阵进行分析，则不难得到以下结论，那就是信号的连续性限制了它的复杂性。下图中（Dst cov 图）左侧为红色曲线所代表的信号的协方差矩阵，矩阵中元素取值的计算方式为测量维度之间的差异并取逻辑函数

$$ Cov \in R^{n \times n}, cov(i, j) = exp(-\lVert v_i - v_j \rVert_2^2) $$

从协方差矩阵的角度来理解信号时，它的每个元素的数值代表信号的两个维度之间的相似性，数值越大代表维度之间的相似性越强，因此它呈现出复杂的纹理。由于其良好的性质我们对它进行 SVD 分解， singular value decomposition - Wolfram|Alpha 其特征值如下图右侧所示。

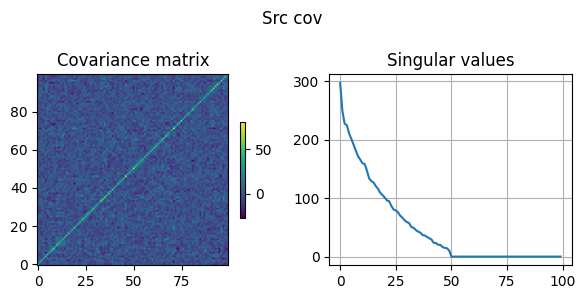
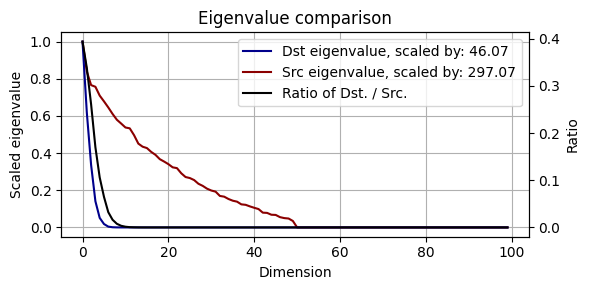
Untitled

Untitled

之所以说“信号的连续性限制了它的复杂性”，这是因为我还计算了随机噪声的协方差矩阵，如 Src cov 图所示。我们通过对两者进行对比不难发现，虽然信号的协方差矩阵看上去比较复杂，但其非零特征值分布更加集中，这代表有意义的信号处于更低秩的状态，说明其背后的逻辑更加简单。二组特征值之间的差异如下图所示。从这个观点来看，噪声比信号更加复杂，那么我们用复杂的噪声去表达简单的信号，这个思路应该是可行的。

Untitled

利用协方差重塑噪声

接下来，我们将验证这种可行性，要做的事情就是找到一组与信号的协方差矩阵相同的噪声。这个事情不难做，过程如附录所示，下图展示了变换后的噪声信号的协方差矩阵。再下面一张图展示了新噪声信号与信号之间的对比关系。由于噪声与信号具有相同的协方差矩阵，因此我们可以说它们具有相似的分布，分布相似性可以从图中看到。那么我们有理由相信，从这组噪声中进行随机采样，采样得到目标信号的概率无疑得到了提升。

Untitled

Untitled

附录：协方差矩阵及其变换

信号及协方差矩阵的定义

$$ X \in R^{m, n} $$

$$ Cov(X) = (X-\mu)^T (X - \mu) $$

生成初始噪声，其协方差矩阵为单位矩阵

$$ i.i.d \rightarrow \begin{cases} X_{1, 2, ... n} \in R^m \sim \mathcal{N}(\mu, \sigma^2) \\ \sigma=1 \end{cases} \rightarrow Cov(X) = I $$

协方差矩阵的 SVD 分解

$$ Cov(X) := C = U \Lambda V^T $$

协方差矩阵及其 SVD 分解必然具有以下性质

$$ \begin{cases} \Lambda_{1, 2, ..., n} \ge 0 \\ U^T U = I \\ V^T V = I \end{cases} $$

通过矩阵变换对噪声进行变换，变换结果是得到一组新的噪声，其协方差矩阵为给定矩阵。

$$ \begin{cases} C = U \Lambda V^T\\ C_1 = U_1 \Lambda_1 V_1^T \end{cases} $$

$$ \Lambda_1 = \Psi \Lambda \Psi, \Psi = \Psi^T $$

$$ \begin{cases} X^TX &= U\Lambda V^T \\ U^T X^T X V &= \Lambda \\ \Psi U^T X^T X V \Psi &= \Lambda_1 \\ U_1 \Psi U^T X^T X V \Psi V_1^T &= U_1 \Lambda_1 V_1^T\\ (U_1 \Psi U^T X^T) (X V \Psi V_1^T) &= C_1\\ \end{cases} $$

$$ f_{C \rightarrow C_1}(X) = X V \Psi V_1^T $$

扩散模型的扩散过程

从如前文所述的例子观点来看，随机信号是方差的游戏。在实际场景中，我们很难事先知道协方差矩阵的精确值，事实上我们往往需要用对角矩阵来模拟它。而扩散模型则有希望完成两者之间的跨越。

我们将扩散过程看作是在一系列均值为零的高维空间中不断采样，这些采样的累积效应将信号扩散到标准正态空间中。最终将扩散过程理解成这样一个动态过程，它不断地、蚂蚁搬家式地将先验信号$X_0$的协方差矩阵“替换”为标准正态分布的协方差矩阵。

我想在这里吐个槽，初学数理统计时喜欢算均值，觉得方差是碍事的东西，但越学越反过来，开始觉得数理统计是研究方差的学问，均值是妨碍我理解它的绊脚石。

扩散过程的递归表示

首先，满足多维高斯的随机变量总可以表示成如下形式

$$ X \sim \mathcal{N}(\mu, \Sigma) \rightarrow p(x) = \mathcal{N}(x; \mu, \Sigma), x \in R^n $$

而扩散过程总是从某个状态开始，以近似微分的方式向新的状态“演变”，演变的终点是噪声。这个过程可以表示成条件概率的形式

$$ \begin{cases} p(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)\\ \lim_{t \rightarrow \infty} q(x_t) = \mathcal{N}(x; 0, I) \\ \beta_1 < \beta_2 < ... < \beta_t < \mathcal{C} \end{cases} $$

乍看起来，第一个式子所代表的扩散过程是均值和方差都在不断变化的过程，最终回归到噪声。但这样的想法立即产生了矛盾，因为这个过程要求扩散过程遵循某种规律，这种规律需要“巧合地”将原始信号回归到噪声。

这种规律无疑是违背随机性的，因为你不能既要求随机性，又要求随机性满足数据的特征。

下面我们将着手拆解这个矛盾，拆解的第一步是将均值去掉。

从方差的角度理解扩散递归

细细想来，我们似乎能够从方差的角度重新理解这个过程，而这个过程与均值没有关系，我们将扩散过程看作是在一系列均值为零的高维空间中不断采样，这些采样的累积效应将信号扩散到标准正态空间中。

首先，将协方差矩阵简化，将其均值项置零

$$ \Sigma = (X-\mu)^T(X - \mu) \rightarrow \Sigma = X^T X $$

接下来，考虑将两个这样的随机变量加权求和

$$ Y = a X_1 + b X_2 $$

其协方差矩阵为

$$ \Sigma_Y = (a X_1 + b X_2) ^T (a X_1 + b X_2) = a^2 \Sigma_1 + b^2 \Sigma_2 + 2ab \cdot \mathcal{Cov}(X_1, X_2) $$

由于两个随机变量相互独立，因此有

$$ \Sigma_Y = a^2 \Sigma_1 + b^2 \Sigma_2 $$

回到扩散过程，我们将均值项看作是 $X_1$ 的一次采样，而方差项看作是随机变量 $X_2$，则有

$$ \begin{cases} x_{t-1} \sim X_1\\ a = \sqrt{1 - \beta_t}\\ b = \beta_t \end{cases} \rightarrow \Sigma_{X_t} = (1 - \beta_t) \Sigma_{t-1} + \beta_t I $$

这样变换的原因是采样虽然会导致随机变量固定下来，但采样之间是随机的，因此对扩散过程来说，它的第一项变化还是可以用随机变量来表示，也就是说，独立采样多次的高维变量，其取值概率等同于其原始分布。你看，如果排除到均值的干扰，这个式子看着就顺眼多了。

通过链式推导实现状态跨越

接下来，我通过链式推导让它更规范一些

$$ \begin{cases} \Sigma_{t} = (1 - \beta_t) \Sigma_{t-1} + \beta_t I \\ \Sigma_{t-1} = (1 - \beta_{t-1}) \Sigma_{t-2} + \beta_{t-1} I \end{cases} $$

将上式进行代入，则有以下迭代式

$$ \begin{cases} \Sigma_t & = a \Sigma_{t-2} + b I \\ \Sigma_{t-2} &: a = (1 - \beta_t)(1 - \beta_{t-1})\\ I &: b = 1 - (1 - \beta_t)(1 - \beta_{t-1}) \end{cases} $$

定义新变量

$$ \begin{cases} \bar{\alpha}t := \Pi{s=1}^t \alpha_s \ \alpha_t := 1 - \beta_t \end{cases} $$

由$\beta$序列的性质可知，$\alpha$序列是缓慢降低的序列$\alpha: 1 \rightarrow 0$。将其代回迭代式，则有

$$ \Sigma_t = \bar{\alpha}_t \Sigma_0 + (1 - \bar{\alpha}_t) I $$

易知

$$ p(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t) I) $$

因此，我们可以将扩散过程理解成这样一个动态过程，它不断地、蚂蚁搬家式地将先验信号$X_0$的协方差矩阵“替换”为标准正态分布的协方差矩阵。最后一块拼图，先验信号怎么来的？答案很简单，它是从协方差矩阵未知的高维正态分布采样得来的。

扩散模型的信号生成实践

本文在前文的基础上开始实践扩散模型，实践的目标是让扩散模型的学习到一条给定的连续曲线，它指代一个 50 维的连续信号。

信号生成及扩散参数

模拟信号是若干个单一频率信号的加权求和，这些频率值和加权系数是随机的。而扩散过程的参数轨迹如右图所示，扩散次数为 100 次，扩散速度参数 $\beta_{max} = 0.1$

$$ \begin{cases} \beta_t = sigmoid(f(t)) * \beta_{max} \\ sigmoid(x) = \frac{1}{1 + exp(-x)} \end{cases} $$

其中，$f(t)$ 代表 $t$ 时刻的扩散参数，它满足线性关系

$$ f(t) = \frac{t-t_{min}}{t_{max} - t{min}} * (t_{max} - t_{min}) + t_{min} $$

扩散模型的训练过程

前文已经总结了扩散次数与原始信号之间的关系，从这个关系可以看到，不管当前处于哪个扩散阶段 $t$，我们都能根据下式将其拆分为信号与噪声的线性组合，线性组合的系数是根据 $\beta_t$ 序列唯一确定的

$$ \begin{cases} \bar{\alpha}t := \Pi{s=1}^t \alpha_s \ \alpha_t := 1 - \beta_t \ p(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t) I) \end{cases} $$

从最实用的角度上讲，扩散模型的学习目标是通过模型预测扩散终点，即噪声。因此，其损失函数为

$$ \hat{N} = \lim_{t \rightarrow \infty} x_t = f_{\theta, x_0}(x_t, t) $$

其中，$\theta$代表网络参数，$x_0$代表初始的有意义的高维信号，$x_t$代表扩散过程中观测到的信号，$N \sim \mathcal{N}(0, I)$ 代表最终噪声。易知，损失函数为

$$ \hat{\theta} = argmin_{\theta} \Vert \hat{N} - N \Vert $$

当然，在训练过程中需要对扩散过程进行大量重复，从而增强模型的鲁棒性。模型训练效果如下，从噪声中还原信号是扩散的逆过程，还原过程用到了下式的逆过程

$$ p(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) $$

Untitled

扩散模型的图像生成实践

本部分尝试从随机噪声“生成”有意义的图像或者数据。

损失函数与扩散链

所谓“有意义”的信号或图像是这样一组随机变量，它的取值服从特定的概率分布

$$ X_t \sim \Psi $$

在该分布中的每一次采样就是对图像的生成。在扩散模型中，我们将该分布作为初始分布，将标准正态分布作为目标分布。在扩散模型中，我们假设它是一个链式反应

$$ X_t = f(X_{t-1}) $$

而它的简单版本为

$$ X_t = \sqrt{\bar{\alpha_t}} \cdot X_0 + \sqrt{1-\bar{\alpha_t}} \cdot \mathcal{Z} $$

而在逆过程中，我们能够从服从标准正态分布的“噪声”出发，生成有意义的图像。达到这一目的的手段是将上面的链条反过来即可

$$ X_{t-1} = f^{-1}(X_t) $$

但它不再有简单版本，因为我们没有正态分布进行训练。因此，我们得到损失函数如下。易见，该损失就是分布之间的 KL 散度。

$$ D_{KL}(\Psi, \Phi) = \mathbb{E}(log(\Psi) - log(\Phi)) $$

其中，$Y_t \sim \Phi$代表观测到数据的经验分布。在理想条件下它“应该”是我们所追求的“有意义”的分布

$$ \mathbb{E}(\Psi - \Phi) = 0 $$

反扩散的样例

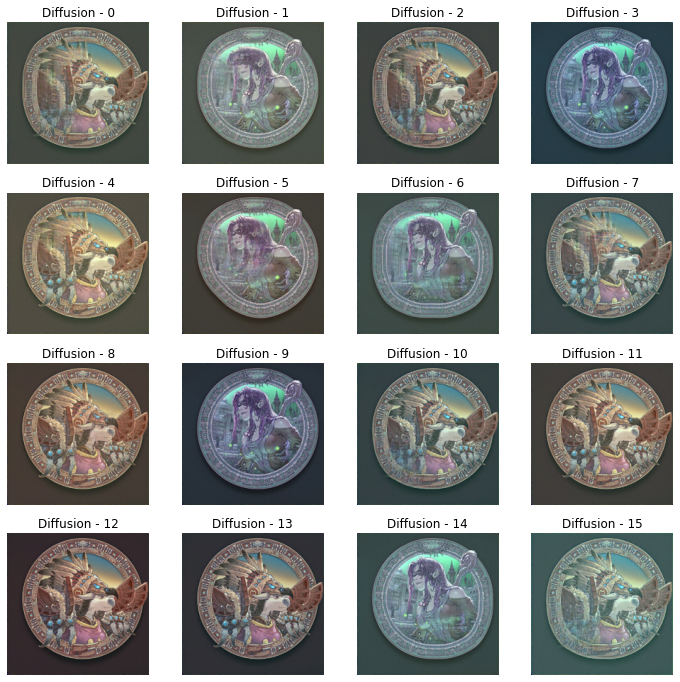
本样例使用 U-net 作为扩散模型的基本算子，用于小步长迭代。在若干次迭代后，得到的终止值就是扩散结果。本例使用的目标图像如下

pic1

因为我手上的计算资源有限，因此用少量图像进行训练，可以得到如下的扩散结果。除了不太圆，看上去还挺好的。

pic2

以上单张图片的扩散过程如下

pic3

该模型极其简单，它能够将大量白噪声图像映射到训练图像所在的概率空间中。因此，它的功能类似 VAE 的 decoder。而它的好处是不依赖于 VAE 的 encoder 就可以学习到“中间”层编码的逆变换结果，因此更适合大规模预训练。

扩散模型的理论推导

这里比较无聊，是对扩散逆过程的公式推导。

内容铺垫

之前已经对扩散过程及其参数进行了规定，如下所示

$$ \begin{cases} p(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)\\ \lim_{t \rightarrow \infty} x_t \sim \mathcal{N}(x; 0, I) \\ \beta_1 < \beta_2 < ... < \beta_t < \mathcal{C} \end{cases} $$

$$ \begin{cases} \bar{\alpha}t := \Pi{s=1}^t \alpha_s \ \alpha_t := 1 - \beta_t \end{cases} $$

$$ p(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t) I) $$

在经过网络（参数计为$\theta$）计算后，我们可以通过 $t$ 次扩散的状态推知最终噪声

$$ \lim_{t \rightarrow \infty} x_t:=\epsilon_\theta = f_\theta(x_t, t), \epsilon_\theta \sim \mathcal{N}(0, I) $$

逆扩散过程

如果我们的目的是从$t$次扩散的结果反推其原因，即把扩散过程逆转过来，则等价于求解条件概率，如下式所示

$$ \begin{cases} p(x_{t-1} | x_t, x_0) &= p(x_t, x_{t-1}|x_0) \cdot \frac{1}{p(x_t | x_0)} \\ p(x_t, x_{t-1}) &= p(x_t | x_{t-1}) \cdot p(x_{t-1}) \\ p(x_t, x_{t-1}) &:= p(x_t, x_{t-1} | x_0)\\ p(x_{t-1}) &:= p(x_{t-1} | x_0) \end{cases} $$

因此有简化式

$$ p(x_{t-1} | x_t) = \frac{p(x_t | x_{t-1}) p(x_{t-1})}{p(x_t)} $$

由于多维正态分布具有统一的形式，因此在求解上式时，我们可以只需考虑指数项之间的加法关系

$$ X \sim \mathcal{N}(\mu, \Sigma) \rightarrow p(x) = C \cdot exp(-(x - \mu)^T \Sigma (x - \mu)), \int p(x) dx = 1 $$

条件概率的指数项为

$$ (x_t - \sqrt{1 - \beta_t}\cdot x_{t-1})^T \beta_t^{-1} (x_t - \sqrt{1 - \beta_t}\cdot x_{t-1}) + (x_{t-1} - \sqrt{\bar{\alpha}{t-1}} \cdot x_0)^T (1-\bar{\alpha}{t-1})^{-1} (x_{t-1} - \sqrt{\bar{\alpha}{t-1}} \cdot x_0) - (x{t} - \sqrt{\bar{\alpha}{t}} \cdot x_0)^T (1-\bar{\alpha}{t})^{-1} (x_{t} - \sqrt{\bar{\alpha}_{t}} \cdot x_0) $$

虽然这个式子较为复杂，但我们只关心 $x_{t-1}$的二次项和一次项系数

$$ \begin{cases} x_{t-1}^2 := \psi_2\\ -2x_{t-1} := \psi_1 \end{cases} $$

易知，条件概率的指数项总可以表示为如下形式

$$ (x_{t-1} - \frac{\psi_1}{\psi_2} )^T \psi_2 (x_{t-1} - \frac{\psi_1}{\psi_2}) + \mathcal{C} $$

其中，$\mathcal{C}$ 为待定常数。它代表条件概率密度函数为

$$ p(x_{t-1} | x_t, x_0) = \mathcal{N}(\frac{\psi_1}{\psi_2}, \psi_2^{-1}) := \mathcal{N}(\mu, \Sigma) $$

经推导（过程见附录）得两项系数如下

$$ \begin{cases} \psi_1 = \beta_t^{-1} \sqrt{\alpha_t} \cdot x_t + (1 - \bar{\alpha}{t-1})^{-1} \sqrt{\bar{\alpha}{t-1}} \cdot x_0 \ \psi_2 = \frac{1 - \bar{\alpha}t}{\beta_t(1-\bar{\alpha}{t-1})} \end{cases} $$

因此其协方差矩阵为

$$ \Sigma = I \cdot \frac{1-\bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t $$

其均值为

$$ \mu = x_0 \cdot \frac{\beta_t\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}t} + x_t \cdot \frac{\sqrt{\alpha_t} (1-\bar{\alpha}{t-1})}{1 - \bar{\alpha}_t} $$

该均值即为$x_{t-1}$的估计。

扩散逆过程的数值求解

为了在求解过程中摆脱对$x_0$的依赖，将扩散过程数值化为下式

$$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}t} \cdot \epsilon\theta $$

将 $x_0$ 代入 $\mu$ 式中，则有

$$ \mu = \frac{1}{\sqrt{\alpha}t} ( x_t - \epsilon\theta \cdot \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}) $$

附录：扩散逆过程的数值求解推导

重写$x_0$为

$$ x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} x_t - \frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\bar{\alpha}t}} \epsilon\theta $$

代入原式有

$$ \mu = \frac{\beta_t\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_t} (\frac{1}{\sqrt{\bar{\alpha}_t}} x_t - \frac{\sqrt{1-\bar{\alpha}t}}{\sqrt{\bar{\alpha}t}} \epsilon\theta) + x_t \cdot \frac{\sqrt{\alpha_t} (1-\bar{\alpha}{t-1})}{1 - \bar{\alpha}_t} $$

利用等式关系求得 $\epsilon_\theta$系数为

$$ \bar{\alpha}t = \bar{\alpha}{t-1} \cdot \alpha_t \rightarrow \mu = \epsilon_\theta \cdot \frac{\beta_t}{\sqrt{\alpha_t}\sqrt{1-\bar{\alpha}_t} } + f(x_t) $$

而 $x_t$ 系数为

$$ f(x_t) = \frac{\beta_t\sqrt{\bar{\alpha}{t-1}} + \alpha_t\sqrt{\bar{\alpha}{t-1}}(1-\bar{\alpha}_{t-1})}{\sqrt{\bar{\alpha}_t}(1-\bar{\alpha}_t)} $$

经整理得

$$ f(x_t) = \frac{\sqrt{\bar{\alpha}_{t-1}} (\beta_t + \alpha_t + \bar{\alpha}_t)}{\sqrt{\bar{\alpha}_t}(1-\bar{\alpha}_t)} = \frac{1}{\sqrt{\alpha_t}} $$

最终有

$$ \mu = \frac{1}{\sqrt{\alpha}t} ( x_t - \epsilon\theta \cdot \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}) $$

附录：一次项系数推导

与 $x_{t-1}$有关的多项式系数为

$$ -2 \beta_t^{-1} \sqrt{1 - \beta_t} \cdot x_t - 2 (1 - \bar{\alpha}{t-1})^{-1} \sqrt{\bar{\alpha}{t-1}} \cdot x_0 $$

易知

$$ \psi_1 = \beta_t^{-1} \sqrt{1 - \beta_t} \cdot x_t +(1 - \bar{\alpha}{t-1})^{-1} \sqrt{\bar{\alpha}{t-1}} \cdot x_0 $$

$$ \psi_1 = \beta_t^{-1} \sqrt{\alpha_t} \cdot x_t + (1 - \bar{\alpha}{t-1})^{-1} \sqrt{\bar{\alpha}{t-1}} \cdot x_0 $$

其中用到了恒等关系$\alpha_t + \beta_t = 1$。

附录：二次项系数推导

易知

$$ \psi_2 = (1-\bar{\alpha}_{t-1})^{-1} + \beta_t^{-1}(1 - \beta_t) $$

结过整理和化简得

$$ \psi_2 = \frac{1}{1-\bar{\alpha}_{t-1}} + \frac{\alpha_t}{\beta_t} \ \psi_2 = \frac{\beta_t + \alpha_t - \bar{\alpha}t}{\beta_t(1-\bar{\alpha}{t-1})} \ \psi_2 = \frac{1 - \bar{\alpha}t}{\beta_t(1-\bar{\alpha}{t-1})} $$

其中用到了恒等关系$\alpha_t + \beta_t = 1$。