This repository includes the codes for simple analysis of Finnish Vakio veikkaus (sports betting) data. The data includes results of soccer matches from the weeks and years 37/1972 - 40/2016, coded as "homewin" (1), "draw" (X), "awaywin" (2). One round of betting in Vakio involves predicting 1, X or 2 for 13 matches. This is called a "row".
The analysis focuses on using the data for computing the expected "homewin" probability and then also computes some probabilities of observing inentical rows in the amount of rows found in the data.
rivit <- read.csv2("Tilastot.csv", stringsAsFactors = FALSE)
nrow(rivit)## [1] 2284
table(do.call(c,rivit))##
## 1 2 X
## 13464 8310 7918
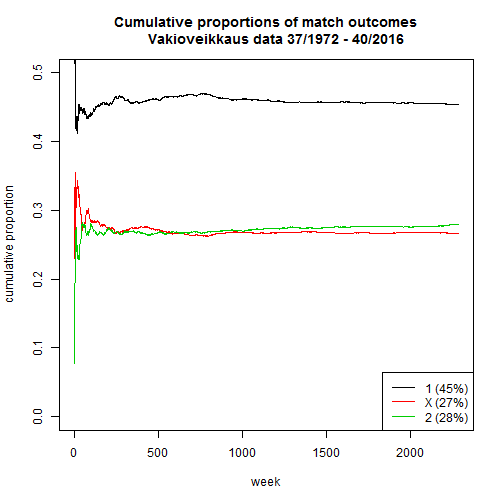
Cumulative proportions of 1, X and 2 outcomes
source("outcome_proportions.R")According to the data, the proportion of hometeam wins ("1") is 0.45 and the proportions of draws and losses are almost identical.
Here we compute the expected frequencies of rows with 0, 1, ..., 13 homewins and then compare to the observed frequencies.
Expected homewins assumption: the probability of a homewin is 0.45 for each match.
source("homewins.R")## expected observed
## 0 1 2
## 1 10 10
## 2 50 47
## 3 151 142
## 4 308 330
## 5 454 427
## 6 495 484
## 7 405 411
## 8 249 252
## 9 113 125
## 10 37 39
## 11 8 13
## 12 1 2
## 13 0 0
The data included three of the same rows, which should be somewhat unlikely because there are
3^13## [1] 1594323
unique possible rows.
The probability of observing three or more identical rows during the years observed in the data was therefore simulated.
A naive approach would be to assume that each possible row is observed with identical probability. Then, the probability would be:
source("p_morethan2identical_naive.R")## [1] 5e-04
However we know that a homewin is more probable than the other outcomes and therefore the distribution of rows is biased towards rows with homewins. In this second simulation, we take this into account and we get a significantly higher probability:
source("p_morethan2identical.R")