Algorithms

Summary

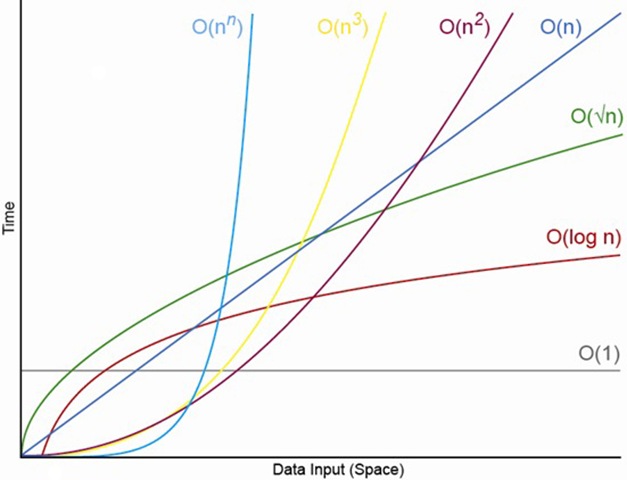
Big-O Notation

Big-O notation is used to compare the efficiency of algorithms and data structures. It provides an upper bound on worst-case runtime and an approximation of how things scale. In general, we find these approximations by counting operations.

Constant time operations (aka O(1), 1 unit of time)

declarations/assignments (let num = 0)
comparisons (num > 0)
object accesses (arr[0])
simple mathematical operations (+, -, &, /)

Examples

Constant time O(1)

let num = 0;
function increment() {
    num = num + 1;
}

linear time O(n), where n is the length of the array

const arr = [0, 1, 2, 3];
function increment(arr) {
    for (let i = 0; i < arr.length; i++) {
        arr[i] = arr[i] + 1;
    }
}

quadratic time O(n^2), where n is the length of the array

const arr = [0, 1, 2, 3];
function sums(arr) {
    const results = [];
    for (let i = 0; i < arr.length; i++) {
        for (let j = 0; j < arr.length; j++) {
            results.push(arr[i] + arr[j]);
        }
    }
}

Big-O is used to approximate how algorithms scale when input-size (array length, number of items in an object, string length, or whatever) grows towards infinity, so you can get rid of constant factors and additive terms with smaller orders of growth. We only want to keep the term that will dominate the function as input-size grows. For example, we say 5n + 2 is O(n) because the coefficient and constant become negligible when n is large.

Recursion

When attempting to solve an algorithm, there are generally two routes you can take: the iterative or the recursive route. A recursive function is simply a function that calls itself. Instead of using a loop to repeat steps and solve the problem iteratively, you can write a recursive function that will use itself to break down the problem into smaller parts and piece together the solution.

Remember the 3 crucial parts of a recursive function:

Base Case
- handle the simplest input
Recursive Call
- call the function on a simpler input
- take a "leap of faith"
  - assume your recursive call with work and use it to solve the bigger problem
Return
- return your result so that you have something to use during your leap of faith

Sorting Algorithms

Bubble Sort O(n^2)

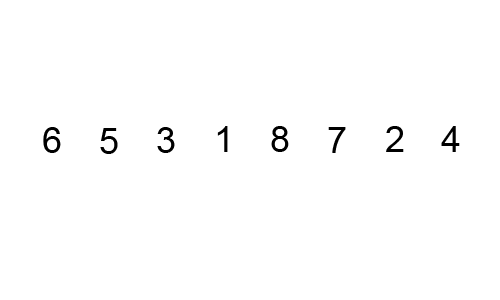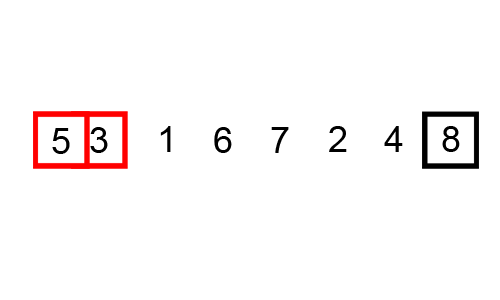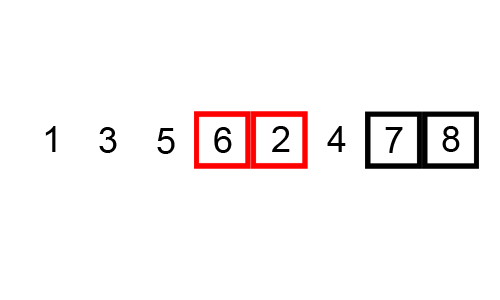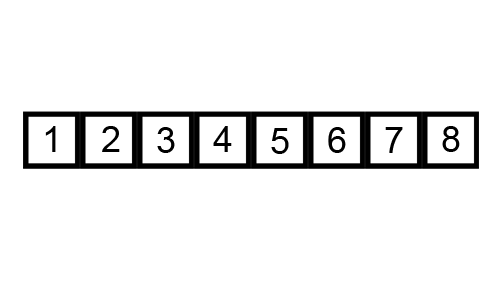
Bubble sort is terribly inefficient, but it has a cute name and is probably the most intuitive. It iterates through the array as many times as needed; it knows to stop once no more changes need to be made (aka the array is sorted). At each iteration, it swaps neighboring elements if they are out of order, and essentially "bubbles" one (biggest, unsorted) element to its correct position.

Insertion Sort O(n^2)

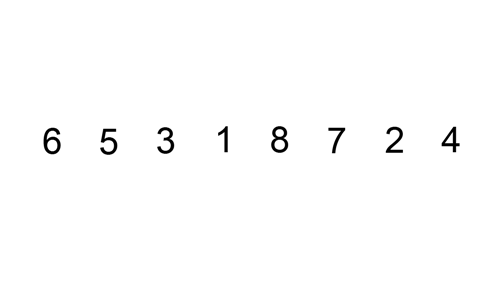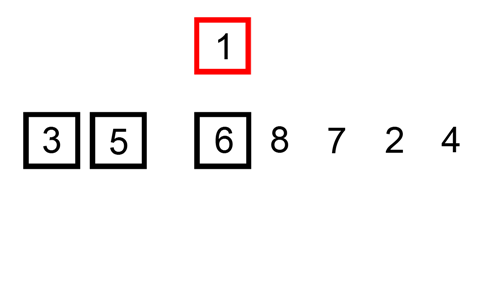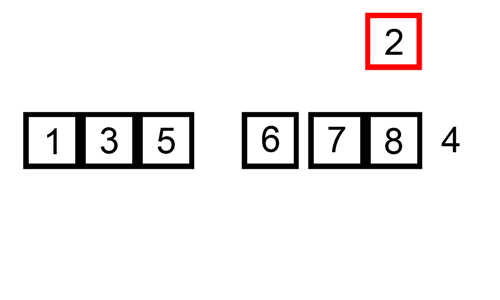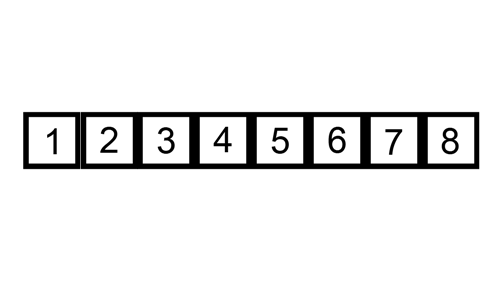
Like bubble sort, insertion sort also assembles a sorted array one element at a time. It takes the next item in the unsorted portion of the array and places it in its correct position in the sorted portion of the array.

Merge Sort O(nlogn)

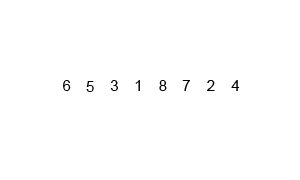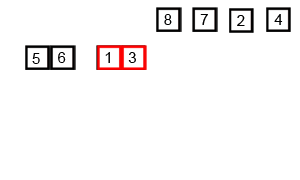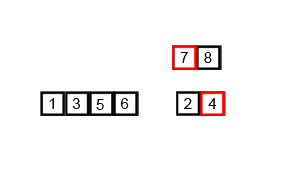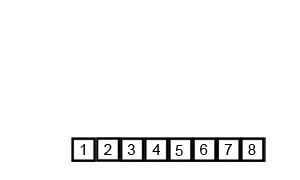
Merge sort is a recursive divide-and-conquer algorithm. It recursively splits the array into two halves and merges them back together in sorted order. Since it is done recursively, the array is broken down until each element is in its own individual array. Then pairs of these one-element arrays are merged so that there is a collection of two-element, sorted arrays. These are then merged in pairs and so on, until all the elements have been pieced back together into one fully sorted array.

How do I get started?

Have BOTH partners fork this repo
- click on the Fork button on the top right of the page
- click on your handle to fork to your repo
Choose one partner's GitHub repo to work from, and clone it to your shared machine
- first, make sure you're on your new forked repo on GitHub
- copy and paste github url from the right side of the page
- enter the following line into your command line and insert your copied url instead of the quoted text:
```
git clone 'copied url'
```

Add two remote links to the cloned repo on your shared workstation: one to CodesmithLLC's repo, and one to the partners repo that was not cloned:

git remote add upstream https://github.com/CodesmithLLC/unit-3-algorithms.git

git remote add partner https://github.com/PARTNERS_GITHUB_HANDLE/unit-3-algorithms.git

Each partner clone their own repo to their own laptop, following the clone instructions in step 2
Each partner add two remote links to their clone on their own laptop, one to CodesmithLLC's repo, and one to their partner's repo, following the instructions in step 3
As you work on the shared workstation, periodically push your changes to your repo with git push origin master. Your partner can then use git pull partner master to get the changes onto their machine, followed by git push origin master to push those changes to their own GitHub repo!
Complete the challenge in located in part1/main.js directory. We recommend completing the algorithms in the order they appear in the tests.
After completing part1, move on to part2/ where you'll find Coin Sum and N-Paths. Complete these problems in whichever order you prefer.

How do I test if my answer is correct?

To test your functions, open index.html in your browser.

NOTE: While completing the challenges, if all tests that previously passed ALL suddenly fail, there is most likely a syntax error in your code. Open Chrome Dev Tool's to locate the cause of the error.

Extension

Done already? If you've passed all the test cases for this unit, make sure that you've analyzed the time complexities of all of your solutions. Can any be optimized? Can you remove nested loops or other inefficiencies for particular algos? Once you've done that, you can go back to unit-2-data-structures and work on some more of those!

Turmbeoz/translatePlugin