scala-lsgo-benchmark is a Scala implementation of the test suite used in the competitions organised by the IEEE Task Force on Large Scale Global Optimization (LGSO) as part of the IEEE Congresses on Evolutionary Computation (CEC).
This implementation of the test suite is based on the original C++ implementation which is available here: lsgo_2013_benchmarks_original.zip. A Matlab implementation and a Java wrapper are also available in the zip file.
Also a Python wrapper for the C++ implementation of the test suite can be found here: https://pypi.python.org/pypi/cec2013lsgo
Detailed information about these benchmark functions is provided in the following technical report:
In order to use the scala-lsgo-benchmark in your Scala project add the following to your build.sbt:
libraryDependencies += "org.apache.commons" % "commons-math3" % "3.3" // this is optional
libraryDependencies += "io.github.xoanpardo" %% "scala-lsgo-benchmarks" % "0.1.2"The Apache Commons Math dependency is only necessary to generate random samples. If you do not plan to use random samples in your code or they are generated by other means it can be skipped.
Note: the original
cdatafilesfrom the C++ implementation are included in the distribution package for convenience.
scala-lsgo-benchmark is very easy to use. For each function class in the benchmark there is a companion object to make it easier to create function instances.
import gal.udc.gac.lsgo2013.Benchmark._
val f1 = F1() // F1 to F15 companion objects are available
val f10 = F10()Also, a benchmark constructor is available to get an instance of all benchmark functions at once.
import gal.udc.gac.lsgo2013.Benchmark._
val lsgo2013 = LSGO2013() // benchmark constructor, returns a Vector of function instances
val f1 = lsgo2013(0) // another way to get a function instance (index is the function ID minus 1)
val f10 = lsgo2013(9)For each benchmark function the following information is accessible:
idthe function name.infoan instance ofSearchSpaceParameterscontaining the search space dimensionality and boundaries.
This information can be obtained in two ways, directly from an instance of the function or from the companion object of its class. The following are examples of both.
import gal.udc.gac.lsgo2013.Benchmark._
val f1 = F1()
val info = f1.info // dimension and boundaries of the search space obtained directly from the function instance
println(s"${f1.id}: (dim=${info.dim}, lower=${info.lower}, upper=${info.upper})") // F1: (dim=1000, lower=-100.0, upper=100.0)import gal.udc.gac.lsgo2013.Benchmark._
val info = F1.info // dimension and boundaries of the search space obtained from the companion object
println(s"${F1.id}: (dim=${info.dim}, lower=${info.lower}, upper=${info.upper})") // F1: (dim=1000, lower=-100.0, upper=100.0)import gal.udc.gac.lsgo2013.Benchmark._
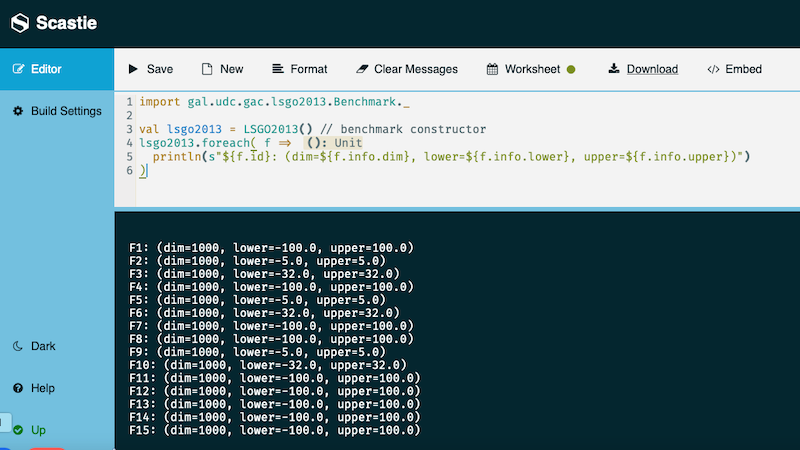
val lsgo2013 = LSGO2013() // benchmark constructor
lsgo2013.foreach( f =>
println(s"${f.id}: (dim=${f.info.dim}, lower=${f.info.lower}, upper=${f.info.upper})")
)Every function class is implemented by extending a base function definition FitnessFunction and overriding its apply method, so they are evaluated in the same way as any other function. The following is an example of how to evaluate a function at zero.
import gal.udc.gac.lsgo2013.Benchmark._
val f1 = F1() // f1 is a FitnessFunction instance
val zero = Vector.fill(f1.info.dim)(0.0) // vector of zeros
val expected = 2.09833896353343505859E+11 // expected result of f1(zero)
assert(f1(zero) == expected) // invoking the apply() method of F1This is an extended version of the previous example in which all the benchmark functions are evaluated at zero.
import gal.udc.gac.lsgo2013.Benchmark._
import gal.udc.gac.lsgo2013.dim // default dimension for all functions
val zero = Vector.fill(dim)(0.0) // vector of zeros
val tolerance: Double = 8.0E-16 // maximum allowed relative round-off error
val solutions = Vector( // expected results (taken from the C++ implementation)
2.09833896353343505859E+11,
4.76203116166061372496E+04,
2.17290025349525564025E+01,
1.07955147656065953125E+14,
4.84191483329246416688E+07,
1.07773246530947787687E+06,
9.93826981321072625000E+14,
5.72227150187806412800E+18,
6.00160320250193595886E+09,
9.81154816487000137568E+07,
1.04485201647212016000E+17,
1.71135423694972143555E+12,
8.27380048985966720000E+16,
4.40797968120962457600E+18,
2.39389233661550150000E+15)
val lsgo2013 = LSGO2013() // benchmark constructor
lsgo2013.zip(solutions) foreach { case (f, expected) => // every function is zipped with its expected result
assert(math.abs(f(zero) - expected) / expected <= tolerance, s"Round-off error greater than tolerance at ${f.id}")
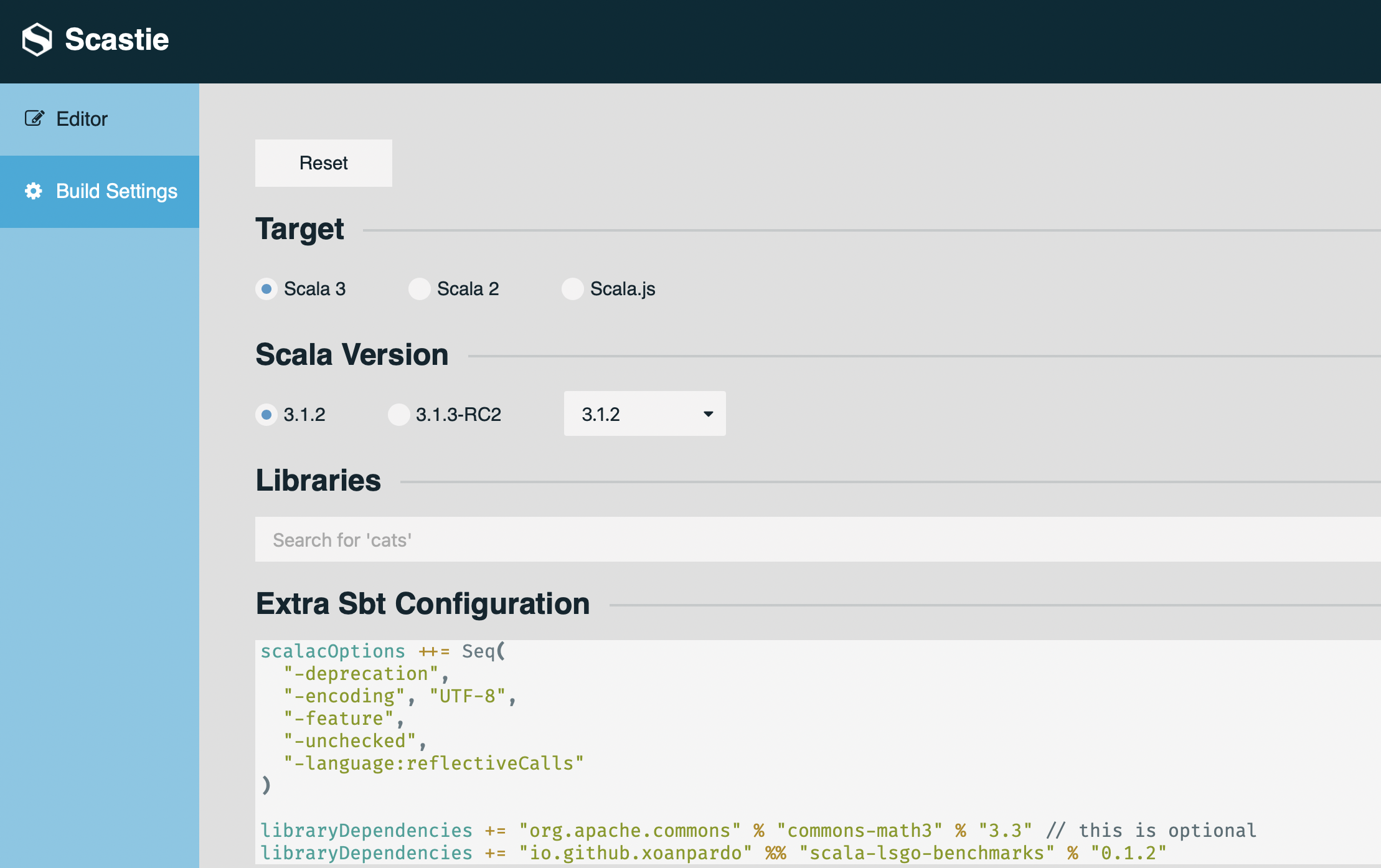
}Want to try scala-lsgo-benchmarks and you don't have Scala? Run the examples in your browser with Scastie.
Follow these steps:
- In Build Settings
- Select the version 2.13.8 of Scala.
- Add the
-language:reflectiveCallsproperty and scala-lsgo-benchmarks library dependencies into the Extra Sbt Configuration field.
The content of the Extra Sbt Configuration field after editing should be:
scalacOptions ++= Seq(
"-deprecation",
"-encoding", "UTF-8",
"-feature",
"-unchecked",
"-language:reflectiveCalls"
)
libraryDependencies += "org.apache.commons" % "commons-math3" % "3.3" // this is optional
libraryDependencies += "io.github.xoanpardo" %% "scala-lsgo-benchmarks" % "0.1.2"- In the Editor, copy the example you want to run and click on the Save button
Included with the test suite there are some helper utilities to generate random samples, to scale vectors to search space boundaries, to read the cdatafiles included in the distribution package and to measure execution times.
In the following there are some examples showing how to use them. For more examples refer to the tests source code in the src/test/scala directory.
The following example shows how to generate a random sample scaled to the search space boundaries of a function.
import gal.udc.gac.lsgo2013.Benchmark._
import gal.udc.gac.lsgo2013.util.Random.reals
import gal.udc.gac.lsgo2013.util.SearchSpace._
val f1 = F1()
val random = Vector.fill(f1.info.dim)(reals.sample()).bound(BoundFunction.scale)(f1.info) // Random vector scaled to the search space boundaries
val sol = f1(random)The utilities used in the example are:
reals, a wrapper of UniformRealDistribution configured to generate random values from a uniform distribution in the range [0.0, 1.0) using a thread-safe MersenneTwister pseudo-random number generator. Also included in the library there areinteger, the counter-part ofrealsfor a binary uniform distribution of integers in the range [0, 1] andgenerator, a wrapper of RandomDataGenerator configured with the same pseudo-random number generator asreals.bound, a method to bound vectors to the search space boundaries that supports different bounding strategies. Vectors in the search space are represented in the library as instances ofElement, that is an alias forVector[Double]. Theboundmethod is added toElementinstances through an implicit definition and the bounding strategy to be applied is provided as an argument of typeBoundingFunction. In the example,BoundFunction.scaleis the bounding strategy that scales a vector of uniform samples in [0.0, 1.0) to the search space boundaries ofF1.
The following example shows how to evaluate a function with its optimal solution. The optimal solution is read from the cdatafile included in the distribution package.
import gal.udc.gac.lsgo2013.Benchmark._
import gal.udc.gac.lsgo2013.util.DataFileReader.CDataFileOps
object Reader extends CDataFileOps
val f1 = F1()
val optimum = Reader.readOptimal(f1.id) // reads the optimum solution from the cdatafile included in the distribution package
val expected = 0.0 // expected result of f1(optimum)
assert(f1(optimum) == expected)The Reader object is defined by extending the trait CDataFileOps which implements the methods to read the cdatafiles included in the distribution package.
There are methods in CDataFileOps for each type of cdatafile (i.e. readPermutations, readSubcomponents, etc).
This trait is mixed into the implementation of the benchmark function classes for each function to read its own cdatafiles when necessary.
For convenience, the library includes also an utility function duration to measure execution times.
Execution times returned by duration are instances of FiniteDuration.
The function has two implementations, one for measuring the execution time of functions or sequences of instructions that return a value and another for functions or sequences of instructions that do not. The following is an example of the former.
import scala.concurrent.duration._
import gal.udc.gac.lsgo2013.Benchmark._
import gal.udc.gac.lsgo2013.util.Random.reals
import gal.udc.gac.lsgo2013.util.SearchSpace._
import gal.udc.gac.lsgo2013.util.duration
val f10 = LSGO2013()(9)
val random = Vector.fill(f10.info.dim)(reals.sample()).bound(BoundFunction.scale)(f10.info) // Random vector scaled to search space boundaries
val (sol, t) = duration(f10(random)) // sol = result of f10(random), t = evaluation time in nanoseconds (an instance of FiniteDuration)
println(s"${f10.id} evaluation result is $sol and took ${t.toUnit(MILLISECONDS)}ms")In this second example we are only interested in the average evaluation time and not in the result of function evaluations, so the second form of the duration function is used.
import scala.concurrent.duration._
import gal.udc.gac.lsgo2013.Benchmark._
import gal.udc.gac.lsgo2013.util.Random.reals
import gal.udc.gac.lsgo2013.util.SearchSpace._
import gal.udc.gac.lsgo2013.util.duration
val f1 = LSGO2013()(0)
val random = Vector.fill(f1.info.dim)(reals.sample()).bound(BoundFunction.scale)(f1.info) // Random vector scaled to search space boundaries
val repeats = 100 // number of function evaluations
val t = duration { // t = evaluation time in nanoseconds (an instance of FiniteDuration)
(1 to repeats).foreach(_ => f1(random))
}
println(s"Average time of $repeats evaluations = ${t.toUnit(MILLISECONDS)/repeats}ms")Note: Scala runs in the JVM so, although not included in the examples, it is recommended to perform some evaluations to warm up the JIT compiler before measuring execution times.
Several tests have been performed to validate the correctness of the Scala implementation by comparing its results with the original C++ implementation:
- Individual tests: the base functions (i.e. Sphere, Rastrigin, Ackley, ...) and the transformation functions (i.e. shifting, ill-conditioning, irregularities, rotation, ...) have been tested individually.
- Combined tests: the transformation functions have been tested in combination with each other (e.g. shifting + oscillation + asymmetry + ill-conditioning).
- Full tests: the benchmark functions has been tested at zero, at their optimal and at random samples.
All the tests that use random samples have been run a minimum of 1.000 times using the same random samples for both the C++ and Scala implementations and the results compared.
For individual tests, it has been found that the result is accurate most of the time and that only for some base functions and transformations, there are a small number of runs (< 5%) with relative errors below or around the machine epsilon (approximated as 2.220446049250313080847263336182E-16 in the computer where the tests were run using the following code):
var e = 1.0
while (1.0 + e > 1.0) e *= 0.5
e *= 2.0
eFor combined and full tests, the results are also accurate in most cases and only a small number of runs (< 5%) have accumulated round-off errors that in all cases are lower than 2.0E-14. The exception is the Ackley-based functions f3, f6 and f10, which have shown the worst results (e.g. f10 is the worst case with an accuracy of 17% and round-off errors up to 6.0E-13).
The source code for the tests is available in src/main/resources/c for the C++ implementation and in src/test/scala for the Scala implementation.
Contact the author if you are interested in the detailed results of the validation tests.
This code is open source software licensed under the GPLv3 License.
Xoán C. Pardo <xoan.pardo@udc.gal>
Computer Architecture Group / CITIC
Universidade da Coruña (UDC)
Spain