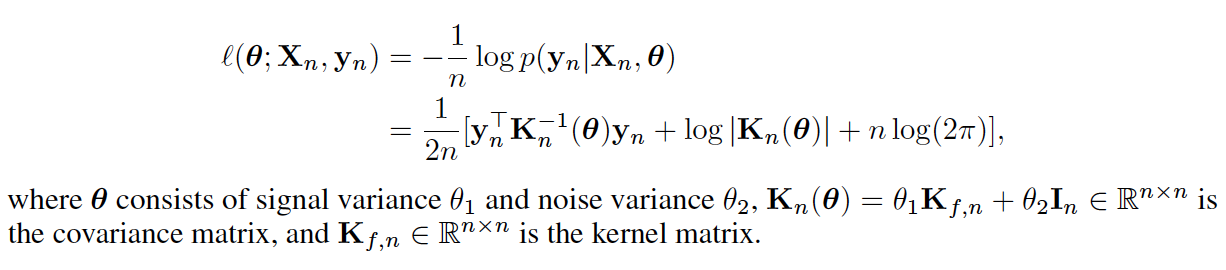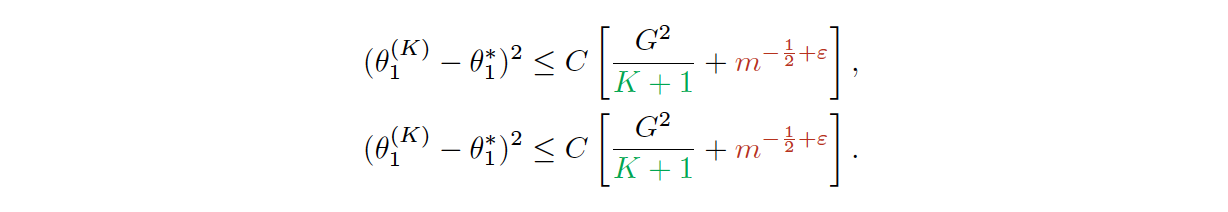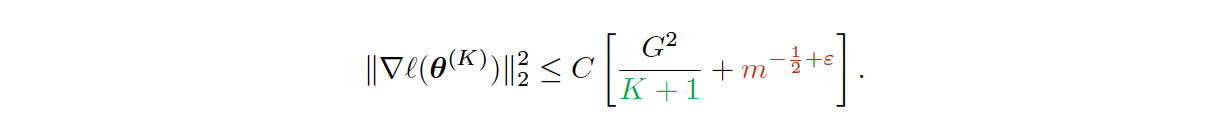UMDataScienceLab/SGD-in-Gaussain-processes

We show that SGD can indeed be used to infer Gaussian processes. This in turn allows GPs to scale far beyond what was thought possible.

SGD in Gaussian Processes

Introduction

• In this project, we apply stochastic gradient descent (SGD) algorithm and its variants to accelerate and improve Gaussian process (GP) inference.
• We provide code for implementing sgGP described in Stochastic Gradient Descent in Correlated Settings: A Study on Gaussian Processes by Hao Chen, Lili Zheng, Raed Al Kontar, Garvesh, Raskutti.

Contributions

• We prove minibatch SGD converges to a critical point of the empirical loss function and recovers model hyperparameters with rate 1/K (K is the number of iterations) up to a statistical error term depending on the minibatch size.
• We prove that the conditional expectation of the loss function given covariates satisfies a relaxed property of strong convexity, which guarantees the 1/K optimization error bound.
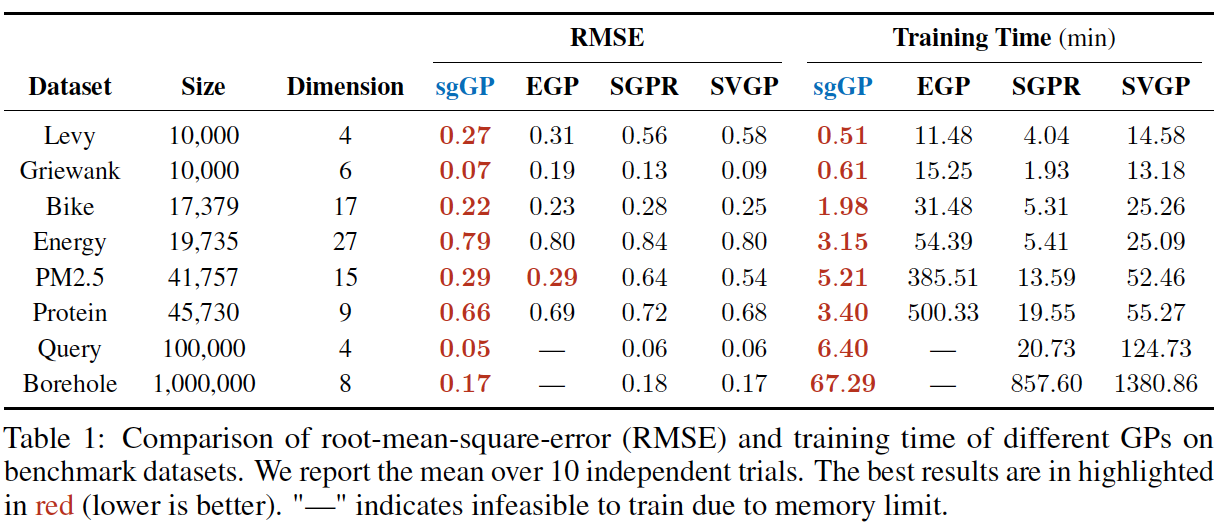
• Computationally, we are able to scale to dataset sizes previously unexplored in GPs in a fraction of time needed for competing methods. Meanwhile statistically, we find that the induced regularization imposed by SGD improves generalization in GPs, specifically in large data settings.

Problem Setup

Loss function

Theoretical Guarantee of Convergence

Assumptions

• Exponential eigendecay. The eigenvalues of the kernel function decay exponentially.
• Bounded iterates. The true parameters and SGD iterates lie within a bounded interval.
• Bounded stochastic gradient. The norm of the stochastic gradient is upper bounded by a constant.

Convergence of parameter iterates

Convergence of full gradient

Numerical Results

Comparison

Illustration

Prerequisite

• R
• dplyr
• RANN

Datasets

• UCI Machine Learning Repository
• Virtual Library of Simulation Experiments