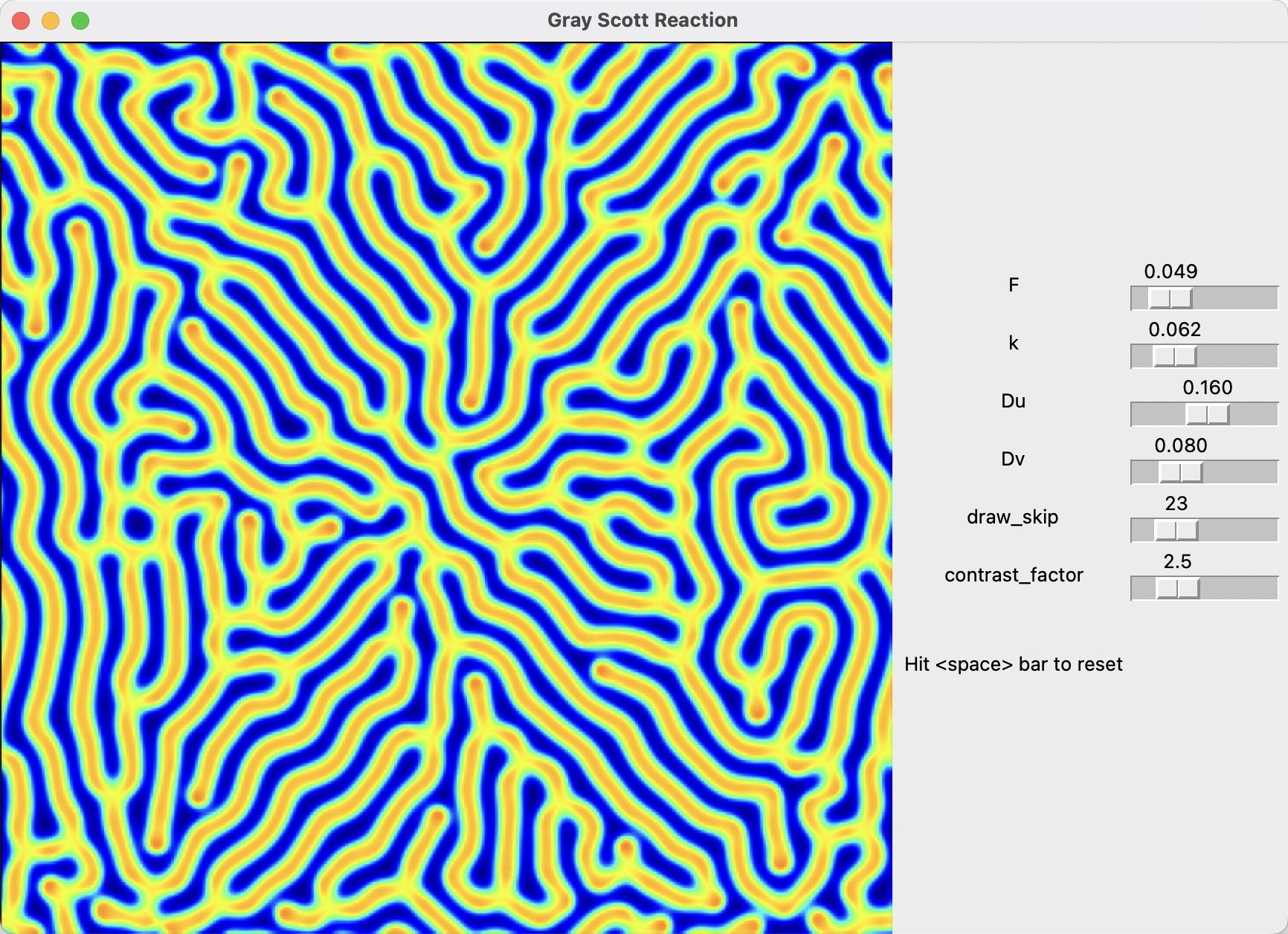
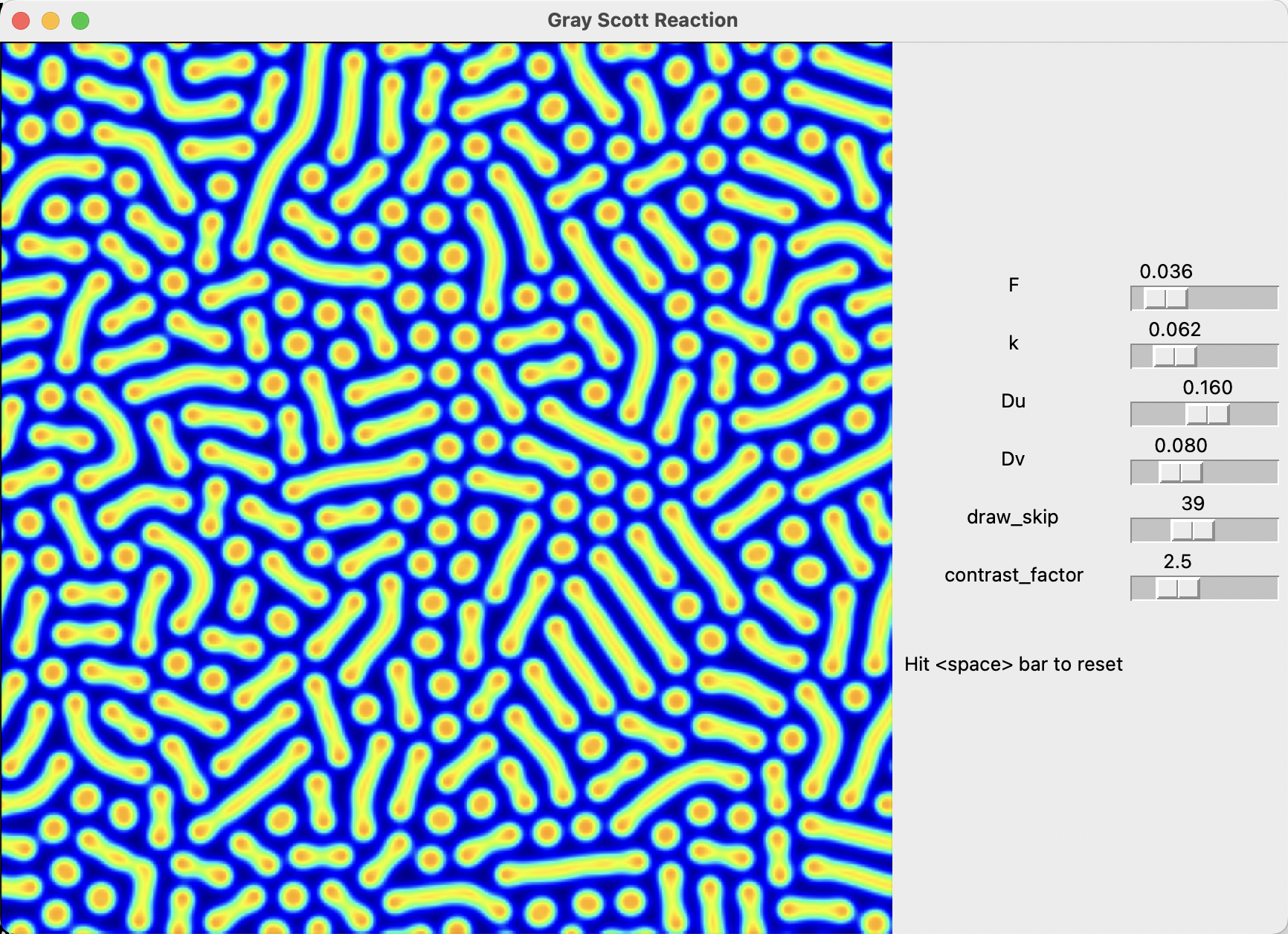
Run the simulation in Tkinter gui by:
$$U + 2V \rightarrow 3V$$
$$\frac{\partial{u}}{\partial{t}} = D_u \nabla^2 u - uv^2 + F (1-u)$$
$$\frac{\partial{v}}{\partial{t}} = D_v \nabla^2 v + uv^2 - (F + k) v$$
where $u(x, y, t)$ and $v(x, y, t)$ are concentrations of the reactants $U$ and $V$.
In the simulation, discrete laplacian operator is used for diffusion, and $dx$ is set to $1$. Time step $dt$ is important for numerical stability when integrating the PDEs, and it must be set to balance efficiency and numerical stability. A theory for this is Courant-Friedrichs-Lewy.