Now that we have discussed different types of graphs, we can begin to discuss a characteristic of a component of the graph: whether two vertices are connected.
Let's go again to wikipedia, to learn a little bit more about this:
Wikipedia tells a couple different things: first that a graph is made up of subgraphs. This makes sense, as a collection of vertices and edges consists of other vertices and edges (sounds like a recursive data structure), and that we call this subset a component of the graph. Finally, it tells us that a connected component exists where there is a path from one part of the component to another.
For example, let's look at our Simpson family tree, but this time we can add in the Flanders family tree as part of our graph of families on The Simpsons.
Grampa (Abe) Simpson
|
Homer - Marge Ned Flanders - Maude Flanders
| | | / \
Bart Lisa Maggie Rod Flanders Todd Flanders
Familial ties on The Simpsons
As you can see while there exists a path from one of the vertexs in the Simpson family tree to another family member, there does not exist a path to any of part of the Flanders family component. So we would say that each vertex representing a Simpsons family member above is part of a connected component, and every vertex representing a Flanders family member consists of a separate connected component.
Determining whether a network is connected is very important. For example, when building a national highway system, if there is exists a highway not connected to another, then that means it is impossible to travel to that highway from another highway. In the context of a social network, this means that there are individuals who do not have a social connection between the two.
There are multiple techniques for exploring the connectivity of a graph. In this lesson, we will discuss breadth first search as one of these techniques.
With breadth first search, we start with a given vertex and mark it as visited. We then visit each of it's adjacent vertices. We then mark that given vertex explored. A vertex is explored if we have visited all of it's adjacent vertexs. A vertex is visited if we have encountered it in our search. We then explore the next vertex.
This is how we decide which vertex to explore next. Each time we visit a vertex, we place it in a queue. We explore the vertex at the front of the queue, and once we explore the vertex we remove it from the queue.
Note: Queue is a data structure where we add and remove elements like people waiting in line at a bank. Elements only get added to the back of the queue, and an element gets removed from the queue only if it was the first element added to the queue. This is referred to as First In First Out (FIFO).
Let's walk through an example of breadth first search.
Let's start with the NYC subway between 8th avenue and Lexington Avenue, and between 42nd street and 14th street, in Manhattan. We want to see if this portion of the graph is connected. As an added bonus, we also will calculate the number of stops between herald square (34th and 6th) and every other stop on our route. This is because with breadth first search, it is fairly easy to also calculate each vertex's distance from the starting distance.
This is our approach. Starting with the only initially visited vertex, the root vertex, and fully explore the root vertex. Then explore each every other visited but unexplored vertex, until every vertex has been visited and explored. Each time, we visit a vertex we can say that it's distance from the root vertex is one more than the distance of the previous vertex.
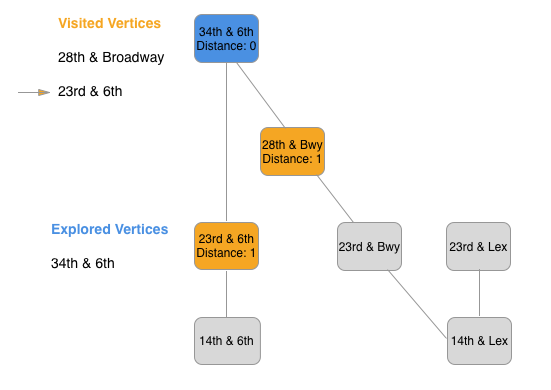
Step 1: Explore 34th & 6th
- Set distance between 34th & 6th and 34th & 6th as zero.
- Explore every other not yet discovered vertex that is adjacent to 34th & 6th. This exploration leads us to discover 28th & Broadway and 23rd & 6th.
- We set their distance from 34th & 6th as one plus the distance of the vertex that led to their discovery. 34th & 6th led to their discovery and its distance was 0. So 1 + 0 = 1, and the distance of 23rd & 6th and 28th & Broadway is 1.
Now take a look at the state of the queue by examining the list under visited nodes. Note that we removed 34th & 6th from our queue of visited vertices when we explored it. We placed 23rd & 6th on top of the queue when we visited it and then 28th & Broadway on top of 23rd & 6th. Following first in first out, we explore the vertex that has been in the queue the longest, 23rd & 6th.
Step 2: Explore 23rd & 6th
- There is one vertex adjacent to 23rd and 6th: 14th & 6th. So we mark 14th and 6th as visited and set its distance from 34th & 6th as 1 + distance of vertex that led to its discovery. So the distance of 14th & 6th from 23rd & 6th is 2.
- We move 23rd & 6th from being a visited vertex to an explored vertex.
- Next up to explore is the bottom most visited vertex, which is 28th and Broadway.
We continue this process until we have no visited vertices left.
So at step 3, we explore 28th & Broadway. This means we visit 23rd & Broadway as it is the only adjacent vertex to 28th & 6th which has not yet been visited. We set the distance to 2 and place it on top of our queue.
| Visited Nodes |
|---|
| 23rd & Broadway |
| 14th & 6th |
At step 4, we explore 14th & 6th, which has no adjacent unvisited vertexs.
| Visited Nodes |
|---|
| 23rd & Broadway |
At step 5, we move on to explore 23rd and Broadway, and find 14th & Lex as the only unvisited vertex.
| Visited Nodes |
|---|
| 14th & Lex |
Then we explore 14th & Lex.
| Visited Nodes |
|---|
| 23rd & Lex |
Finally, we explore 23rd and Lex, which has no adjacent unvisited nodes. And thus when we remove 23rd & Lex from the queue, our queue is empty and our algorithm completes.
| Visited Nodes |
|---|
Ok, so how do we turn something like this into code? Remember that in the previous section we described the graph in terms of the following.
let edges = [
['14th&6th', '23rd&6th'],
['23rd&6th', '34th&6th'],
['34th&6th', '28th&Bwy'],
['28th&Bwy', '23rd&Bwy'],
['23rd&Bwy', '14th&Lex'],
['14th&Lex', '23rd&Lex']
]
let vertices = [
{name: '34th&6th', discovered: null},
{name: '23rd&6th', discovered: null},
{name: '14th&6th', discovered: null},
{name: '28th&Bwy', discovered: null},
{name: '23rd&Bwy', discovered: null},
{name: '14th&Lex', discovered: null},
{name: '23rd&Lex', discovered: null}
]Now for each vertex, we know that we will need to keep track of the of the distance and predecessor so let's change our collection of vertices to the following. We will know if it has a distance, and has been discovered.
let vertices = [
{name: '34th&6th', distance: null, predecessor: null},
{name: '23rd&6th', distance: null, predecessor: null},
{name: '14th&6th', distance: null, predecessor: null},
{name: '28th&Bwy', distance: null, predecessor: null},
{name: '23rd&Bwy', distance: null, predecessor: null},
{name: '14th&Lex', distance: null, predecessor: null},
{name: '23rd&Lex', distance: null, predecessor: null},
]Now let's go back to our procedure. Start at the vertex that we are calculating distance from. Explore a vertex by finding the adjacent vertexs, visit each adjacent vertex and mark it's predecessor. Store the visited vertices that are unexplored in a queue, and then explore the vertex next in the queue. Now break it into steps, and then translate this into code. Give it a shot. We'll go through it in the lab that follows.
When we search a graph, we are determining if a component is connected, meaning there is a path between all of the vertices. With breadth first search we explore the graph by sweeping through it in layers. We accomplish this by placing each node that we visit in a queue, and then exploring each node in the order it was placed into the queue.