qReverse is an architecture-accelerated array reversal algorithm intended as a personal study to design a fast AoS reversal algorithm utilizing SIMD.
| Serial | bswap/rev | SSSE3/Neon | AVX2 | AVX512 | |
| Pattern |  |
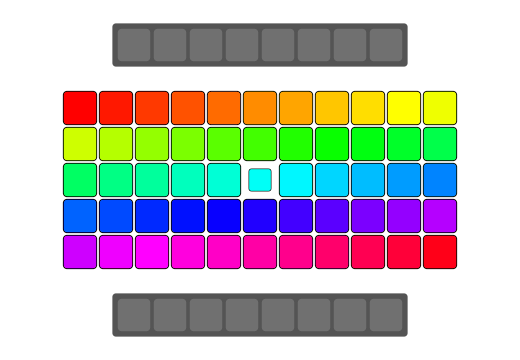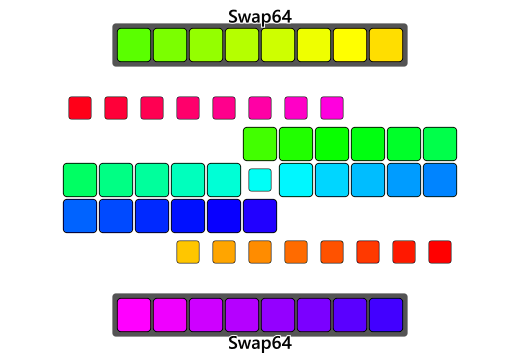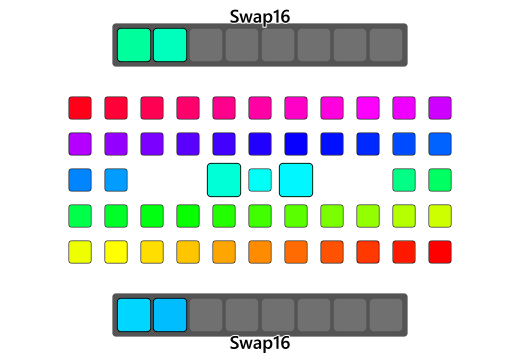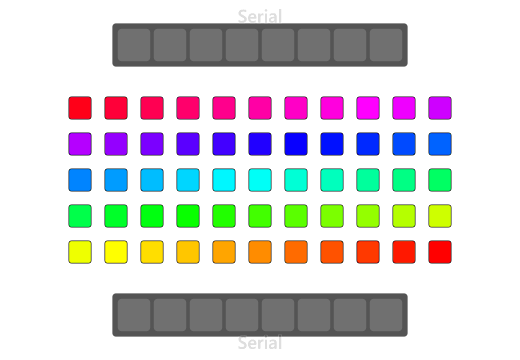 |
 |
 |
 |
| Processor | Speedup | ||||
| i9-7900x | x1 | x15.386 | x10.417 | x22.032 | x22.357 |
| i3-6100 | x1 | x15.8 | x10.5 | x16.053 | - |
| i5-8600K | x1 | x15.905 | x10.21 | x16.076 | - |
| E5-2697 v4 | x1 | x16.701 | x15.716 | x19.141 | - |
| BCM2837 | x1 | x7.391 | x7.718 | - | - |
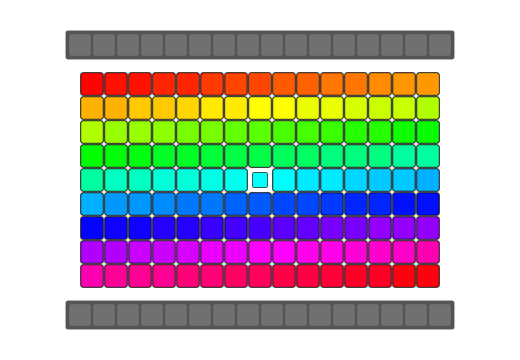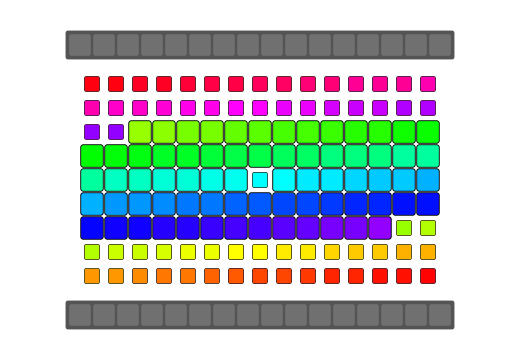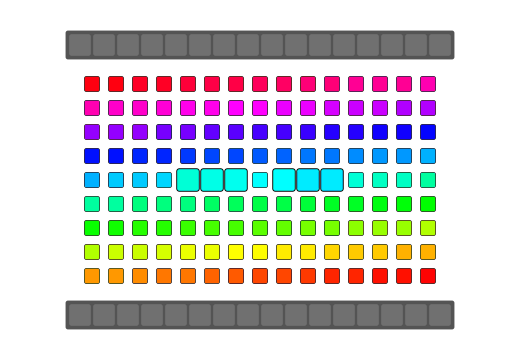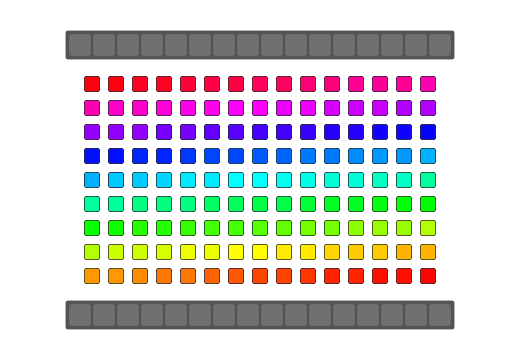
Array reversal implementations typically involve swapping both ends of the array and working down to the middle-most elements. C++ being type-aware treats array elements as objects and will call overloaded class operators such as operator= or a copy by reference constructor where available. Many implementations of a "swap" function would use an intermediate temporary variable to make the exchange which would require a minimum of two calls to an object's operator= and at least one call to an object's copy by reference constructor. Some other novel algorithms use the xor-swap technique after making some assumptions about the data being swapped(integer-data, register-bound, no overrides, etc). std::swap also allows an overload of swap for a type to be used if it is within the same namespace as your type should you want to expose your overloaded method to C++'s standard algorithm library during the reversal
// Taken from http://en.cppreference.com/w/cpp/algorithm/reverse
// Example of using std::reverse
#include <vector>
#include <iostream>
#include <iterator>
#include <algorithm>
int main()
{
std::vector<int> v({1,2,3});
std::reverse(std::begin(v), std::end(v));
std::cout << v[0] << v[1] << v[2] << '\n';
int a[] = {4, 5, 6, 7};
std::reverse(std::begin(a), std::end(a));
std::cout << a[0] << a[1] << a[2] << a[3] << '\n';
}Note that for an odd-numbered amount of elements the middle-most element is already exactly where it needs to be and doesn't need to be moved.
Should std::reverse be called upon a "Plain Ol Data"(POD) type such as std::uint8_t(aka unsigned char) or a plain struct type then compilers can safely assume that your data doesn't have any special assignment/copy overrides to worry about and can treated as raw bytes. This assumption can allow for the compiler to optimize the reversal routine into something simple and much more memcpy-like.
The emitted x86 of a std::reverse on an array of std::uint8_t generally looks something like this.
; std::reverse for std::uint8_t
0x000014a0 cmp rsi, rdi
/=< 0x000014a3 je 0x14c5
| 0x000014a5 sub rsi, 1
| 0x000014a9 cmp rdi, rsi
/==< 0x000014ac jae 0x14c5
.---> 0x000014ae movzx eax, byte [rdi] ; Load two bytes, one from
||| 0x000014b1 movzx edx, byte [rsi] ; each end.
||| 0x000014b4 mov byte [rdi], dl ; Write them at opposite
||| 0x000014b6 mov byte [rsi], al ; ends.
||| 0x000014b8 add rdi, 1 ; Shift index at
||| 0x000014bc sub rsi, 1 ; both ends "inward" toward the middle
||| 0x000014c0 cmp rdi, rsi
\===< 0x000014c3 jb 0x14ae
\\-> 0x000014c5 ret
When making qReverse, the primary interface implements a templated algorithm that follows the same logic. The element-size at compile-time will be templated and emit a pseudo-structure that fits this exact size in an attempt to keep this illustrative implementation as generic as possible for an element of any size in bytes. By having the element-size be templated it will be a lot easier to implement specializations for certain element-sizes while all other non-specialized element sizes fall-back to the serial algorithm. Doing this with a template allows only the proper specializations to be instanced at compile-time as opposed to comparing an element-size variable against a list of available implementations at run-time.
template< std::size_t ElementSize >
inline void qReverse(void* Array, std::size_t Count)
{
// An abstraction to treat the array elements as raw bytes
struct ByteElement
{
std::uint8_t u8[ElementSize];
};
ByteElement* ArrayN = reinterpret_cast<ByteElement*>(Array);
// If compiler adds any padding/alignment bytes(and some do) then assert out
static_assert(
sizeof(ByteElement) == ElementSize,
"ByteElement is pad-aligned and does not match specified element size"
);
// Only iterate through half of the size of the Array
for( std::size_t i = 0; i < Count / 2; ++i )
{
// Exchange the upper and lower element as we work our
// way down to the middle from either end
ByteElement Temp(ArrayN[i]);
ArrayN[i] = ArrayN[Count - i - 1];
ArrayN[Count - i - 1] = Temp;
}
}Emitted assemblies from gcc with certain template specializations:
auto Reverse8 = qReverse<1>;void qReverse<1ul>(void*, unsigned long): mov rcx, rsi shr rcx je .L1 lea rdx, [rsi-1] lea rax, [rdi+rdx] sub rdx, rcx lea rdx, [rdi+rdx] .L3: movzx ecx, BYTE PTR [rdi] ; Load bytes at each end movzx esi, BYTE PTR [rax] sub rax, 1 ; Move indexs "inwards" add rdi, 1 mov BYTE PTR [rdi-1], sil ; Place them at the other end mov BYTE PTR [rax+1], cl cmp rax, rdx ; Loop jne .L3 .L1: rep ret
auto Reverse16 = qReverse<2>;void qReverse<2ul>(void*, unsigned long): mov rdx, rsi shr rdx je .L17 lea rax, [rdi-2+rsi*2] add rdx, rdx mov rsi, rax sub rsi, rdx .L12: movzx edx, WORD PTR [rdi] ; Same as above movzx ecx, WORD PTR [rax] sub rax, 2 add rdi, 2 mov WORD PTR [rdi-2], cx mov WORD PTR [rax+2], dx cmp rax, rsi jne .L12 .L17: rep ret
auto Reverse32 = qReverse<4>;void qReverse<4ul>(void*, unsigned long): mov rdx, rsi shr rdx je .L25 lea rax, [rdi-4+rsi*4] sal rdx, 2 mov rsi, rax sub rsi, rdx .L20: mov edx, DWORD PTR [rdi] ; Same as above mov ecx, DWORD PTR [rax] sub rax, 4 add rdi, 4 mov DWORD PTR [rdi-4], ecx mov DWORD PTR [rax+4], edx cmp rax, rsi jne .L20 .L25: rep ret
auto Reverse24 = qReverse<3>;void qReverse<3ul>(void*, unsigned long): mov rdx, rsi shr rdx je .L25 lea rax, [rsi-3+rsi*2] lea rdx, [rdx+rdx*2] add rax, rdi mov r8, rax sub r8, rdx .L20: movzx esi, WORD PTR [rax] ; Due to the element being 3 bytes movzx ecx, WORD PTR [rdi] ; The arithmetic gets especially weird sub rax, 3 ; But it is still the same movzx edx, BYTE PTR [rdi+2] add rdi, 3 mov WORD PTR [rdi-3], si movzx esi, BYTE PTR [rax+5] mov WORD PTR [rsp-3], cx mov BYTE PTR [rsp-1], dl mov BYTE PTR [rdi-1], sil mov WORD PTR [rax+3], cx mov BYTE PTR [rax+5], dl cmp rax, r8 jne .L20 .L25: rep ret
From here it gets better!
This "plain ol data" assumption can be made for lots of different types of data. Most usages of struct are intended to be treated as "bags of data" and do not have the limitation of additional memory-movement logic for copying or swapping since they are intended only to communicate a structure of interpretation of bytes. The more obvious case-study can also be having an array of chars found in an ASCII string or maybe a row of uint32_t pixel data. If the array elements are aligned to register-sizes(which tend to be powers of 2) then these in-register byte swaps and shuffling can be especially useful. From this point on assume that the array of data is to be interpreted as these "bags of data" instances that do not involve any kind of operator= or Foo (const Foo&) type of overhead logic so the data may be safely interpreted strictly as bytes, think memcpy-like.
Most of the market are running 64-bit or 32-bit machines or have register sizes that are easily much bigger than just 1 byte(the animation above had register sizes that are 4 bytes, which is the size of a single 32-bit register). An observation is that this can speed this up is by loading in a full register-sized chunk of bytes, flipping this chunk of bytes within the register, and then placing it on the other end! Swapping all the bytes in the registers is a popular operation in networking called an endian swap and x86 happens to have just the instruction to do this!
The bswap instruction reverses the individual bytes of a register and is typically used to swap the endian of an integer to exchange between host and network byte-order(see htons,htonl,ntohs,ntohl). Most x86 compilers implement assembly intrinsics that you can put right into your C or C++ code to get the compiler to emit the bswap instruction directly:
MSVC:
_byteswap_uint64_byteswap_ulong_byteswap_ushort
GCC/Clang:
_builtin_bswap64_builtin_bswap32_builtin_bswap16
The x86 header immintrin.h also includes _bswap and _bswap64. Otherwise a more generic and portable implementation can be used as well to be more architecture-generic.
inline std::uint64_t Swap64(std::uint64_t x)
{
return (
((x & 0x00000000000000FF) << 56) |
((x & 0x000000000000FF00) << 40) |
((x & 0x0000000000FF0000) << 24) |
((x & 0x00000000FF000000) << 8) |
((x & 0x000000FF00000000) >> 8) |
((x & 0x0000FF0000000000) >> 24) |
((x & 0x00FF000000000000) >> 40) |
((x & 0xFF00000000000000) >> 56)
);
}
inline std::uint32_t Swap32(std::uint32_t x)
{
return(
((x & 0x000000FF) << 24) |
((x & 0x0000FF00) << 8) |
((x & 0x00FF0000) >> 8) |
((x & 0xFF000000) >> 24)
);
}
inline std::uint16_t Swap16(std::uint16_t x)
{
// This tends to emit a 16-bit `rol` or `ror` instruction
return (
((x & 0x00FF) << 8) |
((x & 0xFF00) >> 8)
);
}Most compilers are able to detect when an in-register endian-swap is being done like above and will emit bswap automatically or a similar intrinsic for your target architecture(The ARM architecture has the rev instruction for armv6 or newer). Note also that bswap16 is basically just a 16-bit rotate of 1 byte which is the rol or ror instruction.
x86_64 (gcc):
Swap64(unsigned long):
mov rax, rdi
bswap rax
ret
Swap32(unsigned int):
mov eax, edi
bswap eax
ret
Swap16(unsigned short):
mov eax, edi
rol ax, 8
ret
x86_64 (clang):
Swap64(unsigned long): # @Swap64(unsigned long)
bswap rdi
mov rax, rdi
ret
Swap32(unsigned int): # @Swap32(unsigned int)
bswap edi
mov eax, edi
ret
Swap16(unsigned short): # @Swap16(unsigned short)
rol di, 8
mov eax, edi
ret
ARM64 (gcc):
Swap64(unsigned long):
rev x0, x0
ret
Swap32(unsigned int):
rev w0, w0
ret
Swap16(unsigned short):
rev16 w0, w0
ret
Using 32-bit bswaps, the algorithm can take a 4-byte chunk of bytes from either end into registers, bswap the register, and then place the reversed chunks at the opposite ends. As the algorithm gets closer to the center it can use smaller 16-bit swaps(aka a 16-bit rotate) should it encounter 2-byte chunks and eventually do serial swaps to anything left over.
and this of course can be expanded into a 64-bit bswap on a 64-bit architecture allowing for even larger chunks to be reversed at once. Once again, first exhaust as many 8-byte swaps, as possible, then do the 4-byte swaps, then the two-2byte swaps, and finally fallback onto the serial 1-byte swaps if need be:
Given an array of 11 bytes to be reversed(odd number, so the middle byte stays the same), divide the array size by two to get the number of single-element swaps to do(using whole-integer arithmetic):
11 / 2 = 5
So 5 single-element serial swaps are needed to reverse this array. Now that there is a way to do 4 element chunks at once too, integer-divide this result 5 again by 4 to know how many four-element swaps needed. The remainder of this division is the number of serial swaps still needed once all the four-element swaps have been exhausted:
5 / 4 = 1
5 % 4 = 1
So only one 4-byte bswap-swap and one naive-swap is needed to fully reverse an 11-element array. Now the 1-byte qReverse template specialization can be added.
// Reverse an array of 1-byte elements(such as std::uint8_t)
// A specialization of the above implementation for 1-byte elements
// Does not call assignment or copy overloads
// Accelerated using - 64,32 and 16 bit bswap instructions
template<>
inline void qReverse<1>(void* Array, std::size_t Count)
{
std::uint8_t* Array8 = reinterpret_cast<std::uint8_t*>(Array);
std::size_t i = 0;
// Using a new iteration variable "j" to illustrate that we know
// the exact amount of times we have to use our chunk-swaps
// BSWAP 64
for( std::size_t j = i / 8; j < ((Count / 2) / 8); ++j )
{
// Get bswapped versions of our Upper and Lower 8-byte chunks
std::uint64_t Lower = Swap64(
*reinterpret_cast<std::uint64_t*>(&Array8[i])
);
std::uint64_t Upper = Swap64(
*reinterpret_cast<std::uint64_t*>(&Array8[Count - i - 8])
);
// Place them at their swapped position
*reinterpret_cast<std::uint64_t*>(&Array8[i]) = Upper;
*reinterpret_cast<std::uint64_t*>(&Array8[Count - i - 8]) = Lower;
// Eight elements at a time
i += 8;
}
// BSWAP 32
for( std::size_t j = i / 4; j < ((Count / 2) / 4); ++j )
{
// Get bswapped versions of our Upper and Lower 4-byte chunks
std::uint32_t Lower = Swap32(
*reinterpret_cast<std::uint32_t*>(&Array8[i])
);
std::uint32_t Upper = Swap32(
*reinterpret_cast<std::uint32_t*>(&Array8[Count - i - 4])
);
// Place them at their swapped position
*reinterpret_cast<std::uint32_t*>(&Array8[i]) = Upper;
*reinterpret_cast<std::uint32_t*>(&Array8[Count - i - 4]) = Lower;
// Four elements at a time
i += 4;
}
// BSWAP 16
for( std::size_t j = i / 2; j < ((Count / 2) / 2); ++j )
{
// Get bswapped versions of our Upper and Lower 4-byte chunks
std::uint16_t Lower = Swap16(
*reinterpret_cast<std::uint16_t*>(&Array8[i])
);
std::uint16_t Upper = Swap16(
*reinterpret_cast<std::uint16_t*>(&Array8[Count - i - 2])
);
// Place them at their swapped position
*reinterpret_cast<std::uint16_t*>(&Array8[i]) = Upper;
*reinterpret_cast<std::uint16_t*>(&Array8[Count - i - 2]) = Lower;
// Two elements at a time
i += 2;
}
// Everything else that we can not do a bswap on, we swap normally
// Naive swaps
for( ; i < Count / 2; ++i )
{
// Exchange the upper and lower element as we work our
// way down to the middle from either end
std::uint8_t Temp(Array8[i]);
Array8[i] = Array8[Count - i - 1];
Array8[Count - i - 1] = Temp;
}
}On some architectures and compilers, the movebe instruction may be emitted which is a CPU instruction that can either read OR write from a memory location AND swap the endian of it, all in one instruction. This instruction is supported since the haswell architecture of intel processors and excavator architecture of AMD processors and will be used automatically if you use -march=native with a processor that supports it.
And now some benchmarks: on a i3-6100 with 8gb of DDR4 ram. I automated the benchmark process across several different array-sizes giving each array-size 10,000 array-reversal trials before getting an average execution time for the given array-size. Using g++ compile flags: -m64 -Ofast -march=native these are the results of comparing the execution time of the current bswap qreverse algorithm against std::reverse:
| Element Count | std::reverse | qReverse | Speedup Factor |
|---|---|---|---|
| 8 | 19 ns | 19 ns | 1.000 |
| 16 | 20 ns | 19 ns | 1.053 |
| 32 | 24 ns | 23 ns | 1.043 |
| 64 | 36 ns | 23 ns | 1.565 |
| 128 | 54 ns | 21 ns | 2.571 |
| 256 | 90 ns | 22 ns | 4.091 |
| 512 | 159 ns | 26 ns | 6.115 |
| 1024 | 298 ns | 35 ns | 8.514 |
| 100 | 43 ns | 21 ns | 2.048 |
| 1000 | 290 ns | 36 ns | 8.056 |
| 10000 | 2740 ns | 191 ns | 14.346 |
| 100000 | 27511 ns | 1739 ns | 15.820 |
| 1000000 | 279525 ns | 24710 ns | 11.312 |
| 59 | 32 ns | 22 ns | 1.455 |
| 79 | 43 ns | 27 ns | 1.593 |
| 173 | 63 ns | 29 ns | 2.172 |
| 6133 | 1680 ns | 127 ns | 13.228 |
| 10177 | 2784 ns | 190 ns | 14.653 |
| 25253 | 6864 ns | 455 ns | 15.086 |
| 31391 | 8548 ns | 564 ns | 15.156 |
| 50432 | 13897 ns | 875 ns | 15.882 |
And so across the board there are speedups up to x15.8! before dipping down a bit for the more larger array sizes potentially due to the accumulation of cache misses with such large amounts of data. The algorithm reaches out to either end of a potentially massive array which lends itself to an accumulation of cache misses at some point. Still a very large and significant speedup over std::reverse consistantly without trying to do some _mm_prefetch arithmetic to get the cache to behave.
The bswap instruction can reverse the byte-order of 2, 4, or 8 bytes, but several x86 extensions later and now it is possible to swap the byte order of 16, 32, even 64 bytes all at once through the use of SIMD. SIMD stands for Single Instruction Multiple Data and allows operation upon multiple lanes of data in parallel using only a single instruction. Much like bswap which atomically reverses all four bytes in a register, SIMD provides an entire instruction set of arithmetic that allows manipulation of multiple instances of data at once in parallel using a single instruction. These chunks of data that are operated upon tend to be called vectors of data. Multiple bytes of data can then be elevated into a vector register to reverse its order and place it on the opposite end similarly to the bswap implementation but with even larger chunks.
These additions to the algorithm will span higher-width chunks of bytes and will be append above the chain of bswap accelerated swap-loops to esure that the largest swaps are exhausted first before the smaller ones. Over the years the x86 architecture has seen many generations of SIMD implementations, improvements, and instruciton sets:
MMX(1996)SSE(1999)SSE2(2001)SSE3(2004)SSSE3(2006)SSE4 a/1/2(2006)AVX(2008)AVX2(2013)AVX512(2015)
Some are kept around for compatibilities sake(MMX) and some are so recent, elusive, or so vendor-specific to Intel or AMD that you're probably not likely to have a processor that features it(SSE4a). Some are very specific to enterprise hardware (such as AVX512) and are not likely to be on consumer hardware either. Other architectures may also have their own implementation of SIMD such as ARM's simd co-processor NEON.
At the moment (July 21, 2017) the steam hardware survey states that 94.42% of all CPUs on Steam feature SSSE3(store.steampowered.com/hwsurvey/). SSSE3 is what will be used as first step into higher SIMD territory. SSSE3 in particular due to its _mm_shuffle_epi8 instruction which lets allows the processor to shuffle bytes within our 128-bit register with relative ease for illustrating this implementation.
SSE stands for "Streaming SIMD Extensions" while SSSE3 stands for "Supplemental Streaming SIMD Extensions 3" which is the fourth iteration of SSE technology. SSE introduces registers that allow for some 128 bit vector arithmetic. In C or C++ code the intent to use these registers is represented using types such as __m128i or __m128d which tell the compiler that any notion of storage for these types should find their place within the 128-bit SSE registers when ever possible. Intrinsics such as _mm_add_epi8 which will add two __m128is together, and treat them as a vector of 8-bit elements are now available within C and C++ code. The i and d found in __m128i and __m128d are to notify intent of the 128-register's interpretation as integer and double respectively. __m128 is assumed to be a vector of four floats by default. Since integer-data is what is being operated upon, the __m128i data type will be used as our data representation which gives access to the _mm_shuffle_epi8 instruction. Note that SSSE3 requires the gcc compile flag -mssse3.
Now to draft a SSSE3 byte swapping implementation and create a simulated 16-byte bswap using SSSE3. First, add #include <tmmintrin.h> in C or C++ code to expose every intrinsic from MMX up until SSSE3 to your current source file. Then, use the instrinsic _mm_loadu_si128 to load an unaligned signed integer vector of 128 bits into a __m128i variable. At a hardware level, unaligned data and aligned data interfaces with the memory hardware slightly differently and can provide for some further slight speedups should data-alignment be guarenteed. No assumption can be made about the alignment of the pointers being passed to qReverse so unaligned memory access will be used. When done with the vector-arithmetic, call an equivalent _mm_storeu_si128 which stores the vector data into an unaligned memory address. This SSSE3 implementation will go right above the previous Swap64 implementation, ensuring that our algorithm exhausts as much of the larger chunks as possible before resorting to the smaller ones:
#include <tmmintrin.h>
...
for( std::size_t j = i / 16; j < ((Count / 2) / 16); ++j )
{
const __m128i ShuffleRev = _mm_set_epi8(
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
);
// Load 16 elements at once into one 16-byte register
__m128i Lower = _mm_loadu_si128(
reinterpret_cast<__m128i*>(&Array8[i])
);
__m128i Upper = _mm_loadu_si128(
reinterpret_cast<__m128i*>(&Array8[Count - i - 16])
);
// Reverse the byte order of our 16-byte vectors
Lower = _mm_shuffle_epi8(Lower, ShuffleRev);
Upper = _mm_shuffle_epi8(Upper, ShuffleRev);
// Place them at their swapped position
_mm_storeu_si128(
reinterpret_cast<__m128i*>(&Array8[i]),
Upper
);
_mm_storeu_si128(
reinterpret_cast<__m128i*>(&Array8[Count - i - 16]),
Lower
);
// 16 elements at a time
i += 16;
}
// Right above the Swap64 implementation...
for( std::size_t j = i / 8; j < ( (Count/2) / 8 ) ; ++j)
...This basically implements a beefed-up 16-byte bswap using SSSE3. The heart of it all is the _mm_shuffle_epi8 instruction which shuffles the vector in the first argument according to the vector of byte-indices found in the second argument and returns this new shuffled vector. A constant vector ShuffleRev is declared using _mm_set_epi8 with each byte set to the index of where it should get its byte from(starting from least significant byte). You might read it as going from 0 to 15 in ascending order but this is actually indexing the bytes in reverse order which gives a fully reversed 16-bit sub-array of bytes.
Now for some speed tests.
| Element Count | std::reverse | qReverse | Speedup Factor |
|---|---|---|---|
| 8 | 19 ns | 19 ns | 1.000 |
| 16 | 22 ns | 20 ns | 1.100 |
| 32 | 27 ns | 20 ns | 1.350 |
| 64 | 37 ns | 21 ns | 1.762 |
| 128 | 55 ns | 23 ns | 2.391 |
| 256 | 91 ns | 24 ns | 3.792 |
| 512 | 158 ns | 31 ns | 5.097 |
| 1024 | 297 ns | 42 ns | 7.071 |
| 100 | 43 ns | 21 ns | 2.048 |
| 1000 | 291 ns | 42 ns | 6.929 |
| 10000 | 2743 ns | 261 ns | 10.510 |
| 100000 | 27523 ns | 2966 ns | 9.280 |
| 1000000 | 279812 ns | 33832 ns | 8.271 |
| 59 | 32 ns | 21 ns | 1.524 |
| 79 | 43 ns | 24 ns | 1.792 |
| 173 | 62 ns | 29 ns | 2.138 |
| 6133 | 1683 ns | 185 ns | 9.097 |
| 10177 | 2787 ns | 291 ns | 9.577 |
| 25253 | 6862 ns | 712 ns | 9.638 |
| 31391 | 8546 ns | 916 ns | 9.330 |
| 50432 | 13893 ns | 1497 ns | 9.281 |
Speedups of up to x10.5!... but this is lower than the bswap version which reached up to x15.8? Maybe some loop unrolling or some prefetching might help this algorithm play nice with the cache. In this implementation only two out of the available 8 registers are being used as well so there is some great room for improvement(Todo)
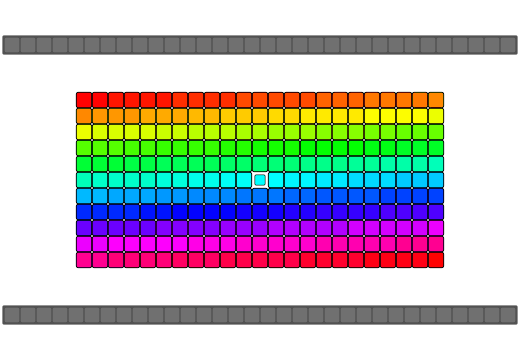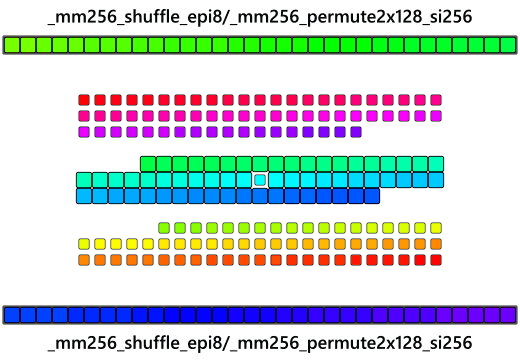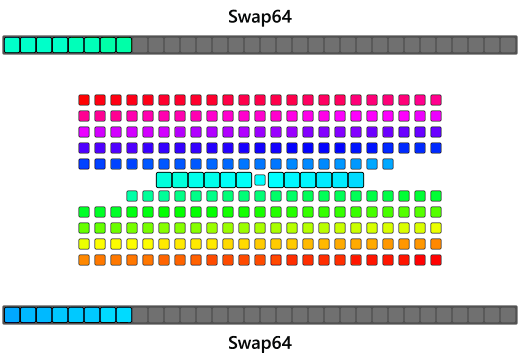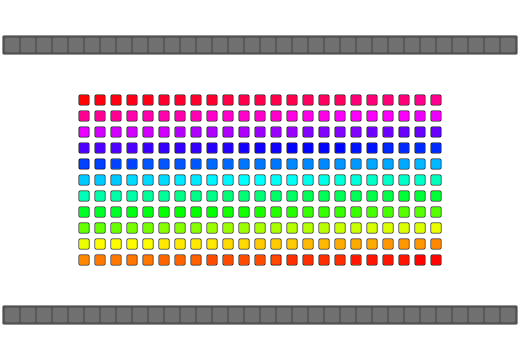
The implementation can go even further to work with the even larger 256-bit registers that the AVX/AVX2 extension provides and reverse 32 byte chunks at a time. The implementation is very similar to the SSSE3 one: load in unaligned data into a 256-bit register using the __m256i type. The issue with AVX/AVX2 is that the 256-bit register is actually two individual 128-bit lanes being operated in parallel as one larger 256-bit register and overlaps in functionality with the SSE register almost as an additional layer of abstraction added upon SSE. Now here's where things get tricky, there is no _mm256_shuffle_epi8 instruction that works like you'd think it would. Since it's just operating on two 128-bit lanes in parallel, AVX/AVX2 instructions introduces a limitation in which some cross-lane arithmetic requires special cross-lane attention. Some instructions will accept 256-bit AVX registers but only actually operates upon 128-bit lanes. The trick here is that rather than trying to reverse a 256-bit register atomically in one go, instead reverse the bytes within the two 128-bit lanes, as if shuffling two 128-bit registers like in the SSSE3 implementation, and then reverse the two 128-bit lanes themselves with whatever cross-lane arithmetic that is available in AVX/AVX2. Note that AVX2 requires the gcc compile flag -mavx2.
_mm256_shuffle_epi8 is an AVX2 instruction that shuffles the two 128-bit lanes of the 256-bit register much like the SSSE3 intrinsic so this can be taken care of first.
const __m256i ShuffleRev = _mm256_set_epi8(
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15, // first 128-bit lane
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15 // second 128-bit lane
);
// Load 32 elements at once into one 32-byte register
__m256i Lower = _mm256_loadu_si256(
reinterpret_cast<__m256i*>(&Array8[i])
);
__m256i Upper = _mm256_loadu_si256(
reinterpret_cast<__m256i*>(&Array8[Count - i - 32])
);
// Reverse each the bytes in each 128-bit lane
Lower = _mm256_shuffle_epi8(Lower,ShuffleRev);
Upper = _mm256_shuffle_epi8(Upper,ShuffleRev);So in the large 256-bit register, the two 128-bit lanes are now reversed, but now the 128-bit lanes themselves must be reversed. _mm256_permute2x128_si256 is another AVX2 instruction that permutes the 128-bit lanes of two 256-bit registers:
Given two big 256-bit vectors and an 8-byte immediate value it can select how the new 256-bit vector it builds is going to be assembled. Pass in the same variable for both of the arguments and "picking" from them as if they were just 2-element arrays of 16-byte elements can simulate a big 128-bit cross-lane swap(think of it like __m128i SomeAVXRegister[2] and going SomeAVXRegister[0] or SomeAVXRegister[1] ). In a way, this is also a big 128-bit "rotate" if you can visualize it.
...
for( std::size_t j = i / 32; j < ((Count / 2) / 32); ++j )
{
const __m256i ShuffleRev = _mm256_set_epi8(
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15
);
// Load 32 elements at once into one 32-byte register
__m256i Lower = _mm256_loadu_si256(
reinterpret_cast<__m256i*>(&Array8[i])
);
__m256i Upper = _mm256_loadu_si256(
reinterpret_cast<__m256i*>(&Array8[Count - i - 32])
);
// Reverse the bytes inside each of the two 16-byte lanes
Lower = _mm256_shuffle_epi8(Lower,ShuffleRev);
Upper = _mm256_shuffle_epi8(Upper,ShuffleRev);
// Reverse the order of the 16-byte lanes
Lower = _mm256_permute2x128_si256(Lower,Lower,1);
Upper = _mm256_permute2x128_si256(Upper,Upper,1);
// Place them at their swapped position
_mm256_storeu_si256(
reinterpret_cast<__m256i*>(&Array8[i]),
Upper
);
_mm256_storeu_si256(
reinterpret_cast<__m256i*>(&Array8[Count - i - 32]),
Lower
);
// 32 elements at a time
i += 32;
}
// Right above the SSSE3 implementation
...Benchmarks:
| Element Count | std::reverse | qReverse | Speedup Factor |
|---|---|---|---|
| 8 | 19 ns | 19 ns | 1.000 |
| 16 | 21 ns | 21 ns | 1.000 |
| 32 | 26 ns | 20 ns | 1.300 |
| 64 | 37 ns | 22 ns | 1.682 |
| 128 | 54 ns | 20 ns | 2.700 |
| 256 | 91 ns | 24 ns | 3.792 |
| 512 | 159 ns | 27 ns | 5.889 |
| 1024 | 298 ns | 36 ns | 8.278 |
| 100 | 45 ns | 20 ns | 2.250 |
| 1000 | 292 ns | 36 ns | 8.111 |
| 10000 | 2739 ns | 189 ns | 14.492 |
| 100000 | 27515 ns | 1714 ns | 16.053 |
| 1000000 | 279701 ns | 25417 ns | 11.004 |
| 59 | 32 ns | 21 ns | 1.524 |
| 79 | 44 ns | 25 ns | 1.760 |
| 173 | 63 ns | 29 ns | 2.172 |
| 6133 | 1681 ns | 127 ns | 13.236 |
| 10177 | 2782 ns | 192 ns | 14.490 |
| 25253 | 6863 ns | 449 ns | 15.285 |
| 31391 | 8545 ns | 556 ns | 15.369 |
| 50432 | 13888 ns | 875 ns | 15.872 |
A speedup of up to x16.053!
AVX512 is particularly rare out in the commercial world. Even so, the algorithm can take that much more of a step forward and operate upon massive 512-bit bit registers. This will allow a swap of 64 bytes of data at once. At the moment, C and C++ compiler implementations of the AVX512 instruction set are spotty at best. There is the benefit of the _mm512_shuffle_epi8 instruction that will allow the shuffling of the four 128-lane registers within the 512-bit register with 8-bit indexes though there is not a confident implementation of _mm512_set_epi8 to be found in MSVC or GCC. There is _mm512_set_epi32 which will require generation of the ShuffleRev constant to use 32-bit integers rather than 8-bit integers. After the initial _mm512_shuffle_epi8 the four lanes still must be reversed due to the need for cross-lane arithmetic so an additional _mm512_permutexvar_epi64 is needed to truely complete the reversal. This is similar to what had to be done for the AVX2 implementation above.
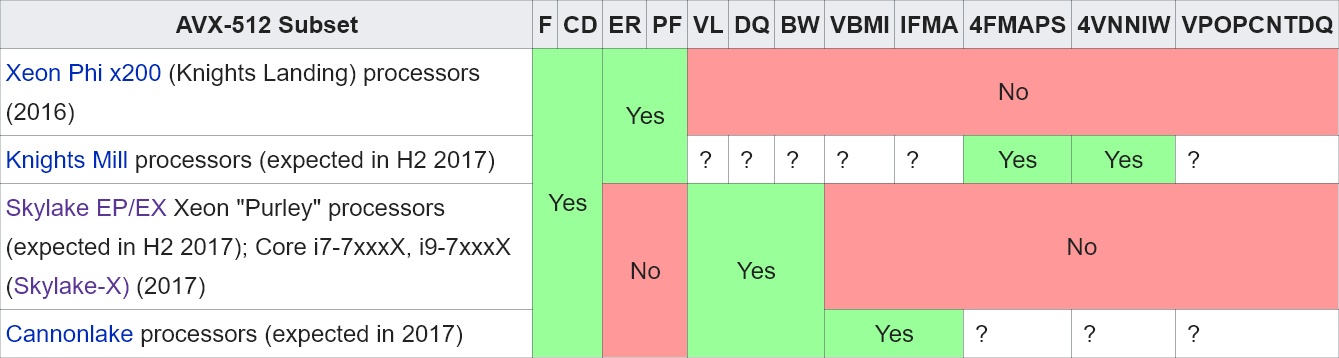
AVX512 is not a single set of instructions. AVX512 has different subsets which may or may not be implemented for a particular processor. For example there is AVX512CD for conflict detection and AVX512ER for exponential and reciprocal instructions though ALL implementations of AVX512 require that AVX512F(AVX-512 Foundation) be implemented. _mm512_shuffle_epi8 is an instruction implemented by the AVX512BW subset which adds Byte and Word operations while _mm512_setepi32 and _mm512_permutexvar_epi64 are AVX512F so _mm512_shuffle_epi8 is the only "stretch" requirement involved here. AVX512BW is currently supported by the current Skylake-X processors and is planned to be implemented more commonly in future processors. For reference, a current map of AVX512 subset implementations(as of September 3, 2017).
In GCC, specific subsets of AVX512 must be enabled using compile flags:
| Subset | Flag |
|---|---|
| Foundation | -mavx512f |
| Prefetch | -mavx512pf |
| Exponential/Reciprocal | -mavx512er |
| Conflict Detection | -mavx512cd |
| Vector Length | -mavx512vl |
| Byte And Word | -mavx512bw |
| Doubleword and Quadword | -mavx512dq |
| Integer Fused Multiply Add | -mavx512ifma |
| Vector Byte Manipulation | -mavx512vbmi |
_mm512_shuffle_epi8 and requires the -mavx512bw flag to compile in gcc while the rest only requires -mavx512f.
// Could have done:
const __m512i ShuffleRev = _mm512_set_epi8(
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
);
// but instead have to do the more awkward:
const __m512i ShuffleRev = _mm512_set_epi32(
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f,
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f,
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f,
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f
);The full AVX512 implementation:
...
for( std::size_t j = i / 64; j < ((Count / 2) / 64); ++j )
{
// Reverses the 16 bytes of the four 128-bit lanes in a 512-bit register
const __m512i ShuffleRev8 = _mm512_set_epi32(
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f,
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f,
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f,
0x00010203, 0x4050607, 0x8090a0b, 0xc0d0e0f
);
// Reverses the four 128-bit lanes of a 512-bit register
const __m512i ShuffleRev64 = _mm512_set_epi64(
1,0,3,2,5,4,7,6
);
// Load 64 elements at once into one 64-byte register
__m512i Lower = _mm512_loadu_si512(
reinterpret_cast<__m512i*>(&Array8[i])
);
__m512i Upper = _mm512_loadu_si512(
reinterpret_cast<__m512i*>(&Array8[Count - i - 64])
);
// Reverse the byte order of each 128-bit lane
Lower = _mm512_shuffle_epi8(Lower,ShuffleRev8);
Upper = _mm512_shuffle_epi8(Upper,ShuffleRev8);
// Reverse the four 128-bit lanes in the 512-bit register
Lower = _mm512_permutexvar_epi64(ShuffleRev64,Lower);
Upper = _mm512_permutexvar_epi64(ShuffleRev64,Upper);
// Place them at their swapped position
_mm512_storeu_si512(
reinterpret_cast<__m512i*>(&Array8[i]),
Upper
);
_mm512_storeu_si512(
reinterpret_cast<__m512i*>(&Array8[Count - i - 64]),
Lower
);
// 64 elements at a time
i += 64;
}
// Above the AVX2 implementation
...Since AVX512 is pretty rare on consumer hardware at the moment: Intel provides an emulator that can provide for some verification that the algorithm properly reverses the array. The emulator is no grounds for a proper hardware benchmark though. After creating a simple test program to verify that the array has been reversed it can be ran through the emulator and verified:
sde64 -mix -no_shared_libs -- ./Verify1 128
Original:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127
Reversed:
127 126 125 124 123 122 121 120 119 118 117 116 115 114 113 112 111 110 109 108 107 106 105 104 103 102 101 100 99 98 97 96 95 94 93 92 91 90 89 88 87 86 85 84 83 82 81 80 79 78 77 76 75 74 73 72 71 70 69 68 67 66 65 64 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
[PASS] Array Reversed
The -mix will cause the software development emulator to audit the execution of the program and the instructions it encounters into a sde-mix-out.txt file. This file is massive by default so -no_shared_libs removes the auditing of shared libraries(such as the standard libraries) from the report. With this the execution summery of qreverse<1> can be examined:
# $dynamic-counts-for-function: void qReverse<1ul>(void*, unsigned long) IMG: /qreverse/build/Verify1 at [0x4e1ffd40a0, 0x4e1ffd4e3e) 1.442%
#
# TID 0
# opcode count
#
...
*isa-set-AVX512BW_512 4
*isa-set-AVX512F_512 6
...
*category-AVX512 4
...
*avx512 10
...
...
VMOVDQA64 2 < Note these are called only twice which
VMOVDQU64 2 makes sense given a 128-byte array
VMOVDQU8 2 and only needing one AVX-512 swap
VPERMQ 2
VPSHUFB 2
*total 75
Not only are the AVX512BW instructions verified to have ran and worked but the entire reversal of 128 elements took only 75 instructions in total!
I recently acquired an Intel i9-7900x BX80673I97900X which features a large portion of the AVX512 subsets and is capable of providing some actual hardware benchmarks for this implementation.
Here the benchmark is compiled using Visual Studio 2017 for x64-Release mode.
| Element Count | std::reverse | qReverse | Speedup Factor |
|---|---|---|---|
| 8 | 63 ns | 59 ns | 1.068 |
| 16 | 62 ns | 61 ns | 1.016 |
| 32 | 74 ns | 59 ns | 1.254 |
| 64 | 104 ns | 61 ns | 1.705 |
| 128 | 80 ns | 18 ns | 4.444 |
| 256 | 90 ns | 20 ns | 4.500 |
| 512 | 157 ns | 22 ns | 7.136 |
| 1024 | 276 ns | 28 ns | 9.857 |
| 100 | 44 ns | 20 ns | 2.200 |
| 1000 | 269 ns | 30 ns | 8.967 |
| 10000 | 2504 ns | 112 ns | 22.357 |
| 100000 | 24222 ns | 1368 ns | 17.706 |
| 1000000 | 236354 ns | 21192 ns | 11.153 |
| 59 | 33 ns | 21 ns | 1.571 |
| 79 | 40 ns | 23 ns | 1.739 |
| 173 | 58 ns | 29 ns | 2.000 |
| 6133 | 1438 ns | 93 ns | 15.462 |
| 10177 | 2481 ns | 147 ns | 16.878 |
| 25253 | 5794 ns | 332 ns | 17.452 |
| 31391 | 7397 ns | 420 ns | 17.612 |
| 50432 | 11915 ns | 858 ns | 13.887 |
A plateau of speedups up to x22.357!
Once we work our way down the middle and end up with something like 4 "middle" elements left then we are just one Swap32 left from having the entire array reversed. What if we worked our way down to the middle and ended up with 5 elements though? This would not be possible actually so long as we have Swap16. 5 middle elements would mean we have one middle element with two elements on either side. Our for( std::size_t j = i/2; j < ( (Count/2) / 2) would catch that and Swap16 the two elements on either side, getting us just 1 element left right in the middle which can stay right where it is within a reversed array(since the middle-most element in an odd-numbered array is our pivot and doesn't have to move anywhere).
Later we can find a way to accelerate our algorithm to have it consider these pivot-cases efficiently so that rather than calling two Swap16s on either half of a 4-byte case it could just call one last Swap32 or even a bigger before it even parks itself in that situation of having to use the naive swap. Something like this could remove the use of the naive swap pretty much entirely.
Here's a little writeup of how to "count" greedy algorithms such as this one!