/game-of-life

Conway's Game of Life on Godot Engine. The game is visualized on a square and on a torus.

Primary LanguageGDScriptMIT LicenseMIT

Conway's Game of Life

Conway's Game of Life implementation in the Godot Engine (v4.2.1).

👾 About Conway's Game of Life

The Game of Life (by John Horton Conway in 1970) is a cellular automaton (a model of computation studied in computational theory) and it's evolution is determined by its initial state.

The game consists of an orthogonal, two-dimensional grid of square cells, each of which is in one of two possible states, alive or dead. Each cell interacts with its neighbors (the cells that are horizontally, vertically, or diagonally adjacent).

At each step one of the following actions occurs:

  • Each live cell with two or three live neighbors moves on to the next generation (surviving).
  • Each live cell with fewer than two live neighbors dies (underpopulated).
  • Each live cell with more than three live neighbors dies (overpopulated).
  • Every dead cell with exactly three live neighbors becomes a live cell (reproduction).

Important

The Game of Life is Turing Complete! 🤩

🍩 Torus

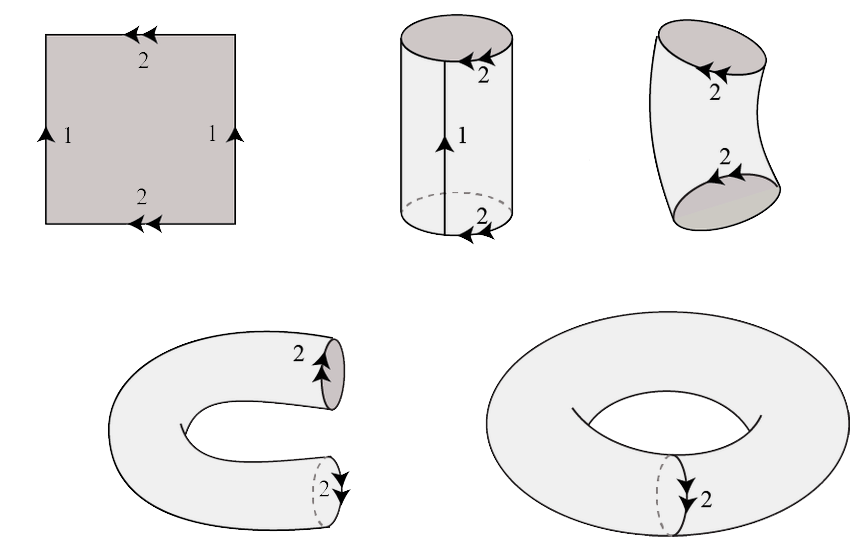
Usually the Game of Life universe is defined as an infinite, two-dimensional, orthogonal grid of square cells, it can also be defined on a topological torus.

A topological torus is a topological space homeomorphic to a torus in Euclidean space. It can be defined as the product of two circumferences $C^1 \times C^2$ or equivalently consider a square and "glue" the opposite sides together. This corresponds to defining on the square $$S = [0, 1] \times [0,1] \subseteq \mathbb{R}^2$$ the equivalence relation $∼_T$ such that $\forall\ p \in [0,1]$ and $B \in \{0,1\}$ $$x ∼_T y \Longleftrightarrow \bigg(x = y\bigg)\ \lor \bigg(x=(B,p) \land y=(1 - B,p) \bigg) \lor \bigg(x=(p,B) \land y=(p,1 - B) \bigg)$$ in other words, is a unique interior point or $x$ and $y$ are on two opposite sides and have an equal coordinate.

With this equivalence relation, we can define the quotient space $S / {∼_T}$ wich is a topological torus.

Topological torus construction from a square

In the case of this project, the field of the game is a two-dimensional finite grid on a square that is converted to a texture and mapped onto the Euclidean torus.

🧮 Computation

Because each iteration of the game of life can require many calculations, particularly if very large grids are used, these are performed in parallel with the Iterative Stencil Loops pattern using a 9-point 2D stencil.

An iterative stencil loop refers to a technique used to update the state of each cell in the grid based on the states of its neighboring cells. The "stencil" refers to the pattern of neighboring cells that are considered when updating each cell's state.

Two grids are initialized, one representing the current state of the cells and the other representing the next state, both grids have the same size. Rules are applied to each cell to calculate the next state grid. Once all cells have been updated, the current state grid is swapped with the next state grid. This ensures that the changes made in the current iteration are reflected in the next iteration. This is repeated for each iteration

🖼️ Screenshots

Simulation with the sample "Gosper's gliders cannon"

screenshot 128 cells

Simulation 128x128 cells, with initial state from a Simplex noise image.

screenshot 128 cells

Simulation 1024x1024 cells, with initial state from a Simplex noise image.

screenshot 1024 cells