/grayscale-conversion

grayscale conversion optimized with OpenMP, SIMD and CUDA

Primary LanguageCMIT LicenseMIT

Report by Dennis Weggenmann and Xiang Rong Lin for the lecture "High Performance Computing" during the winter semester 21/22 at "Hochschule für Technik Stuttgart"

https://github.com/sspeiser/hpc-uebungen

Motivation

RGB to Grayscale conversation is an embarrassingly parallel Problem. So it's perfect for multithreaded programms. Each Pixel can be calculated/converted independently.

GPU

Problems

  • memory transfer between Host and Device
  • when to start measure time ? Before the kernel launch, before the memcopy or before the allocation
  • The first cuda function calls takes a lot of time. For benchmarking reasons i just call a cudaFree(0). Now the first cuda call (most of the time its cudaMalloc) takes for example 0,023 seconds instead of 0,153 seconds
  • cudaHostRegister was not able to allocate enough memory but after trying it 10 times its working

Implementation

GPU Workflow

Host = CPU

Device = GPU

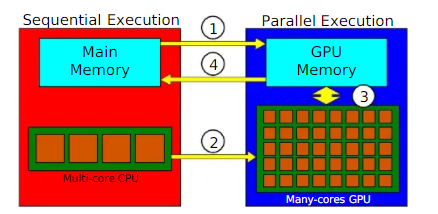
The GPU needs to acces the Data from the main memory. Then the CPU instructs the GPU. The calculation will be parallel executed in cores and the result will be copied back to the main memory.

cuda_profiling https://www.academia.edu/20415057/Parallel_Implementation_of_Grayscale_Conversion_in_Graphics_Hardware

Thread

Each Thread gets mapped to one cuda core

Blocks:

Threads are grouped into Blocks

Grids:

Blocks are grouped into a Grid

Each Kernel launch creates one single Grid

cuda_profiling

https://developer-blogs.nvidia.com/wp-content/uploads/2020/06/kernel-execution-on-gpu-1-625x438.png

We have an input image which is loaded by stbi_load and returns an unsigned char. Then we allocate memory for our grayscale image which the results will be copied in

So now we need to allocate memory for our RGB image on the Device. We do this with CudaMalloc

cudaMalloc(&device_rgb, sizeof(uchar3) * pixel_size*3 );

we also allocate memory for our greyimage on the Device with

cudaMalloc(&device_grey, sizeof(unsigned char) * pixel_size);

with cudaMemcpy the Imagedata will be copied to the memory we allocated for our RBG image. We also have to pass the size of the copied data and in which direction we are going to copy.

cudaMemcpy(device_rgb, Image, sizeof(unsigned char) * pixel_size*3 , cudaMemcpyHostToDevice);

Now the data is in the GPU memory and we are able to launch our kernel.

We are on the Device now

A Kernelfunction looks like a normal function but has a global keyword befor it. With the global identifer we define a function that will run on the Device.

ConvertToGrey<<<Grid, Block>>>(device_rgb, device_grey, rows, columns);

As parameters we pass our already allocated device_rgb and device_grey references and the rows and columns which are basically the width and height of our image. If we take a look at the Kernel function the first thing we see is this

int index_x = threadIdx.x + blockIdx.x * blockDim.x;

ThreadIdx, blockIdx and blockDim are cuda variables. We can access them when we run on the Device. threadIdx : thread index in the block blockIdx : block index in the grid blockDim : number of threads by blocks.

We want the unique Grid index of a thread because threadIdx is only unique in its own Thread Block. So we multiply the Blocks index with the block dimension and add the Threadindex. We do the same for the y index. And now we have the current pixel location

1d coordinate of the greyscale image

int output_offset = index_y * columns + index_x;

now we write the result into the outputimage

 output[output_offset] = rgb.x * 0.299f +rgb.y* 0.587f +rgb.z * 0.114f

we are back on the Host now

The kernel call is asynchronous. But in our case this doesnt bother us because we only have one stream so cudaMemcpy waits until the GPU has finished. Now we copy the data back from the Device to the Host

cudaMemcpy(host_grey, device_grey, sizeof(unsigned char) * pixel_size, cudaMemcpyDeviceToHost);

in the end we need to free the allocated memory on the Device

cudaFree(device_rgb);
cudaFree(device_grey);

Review

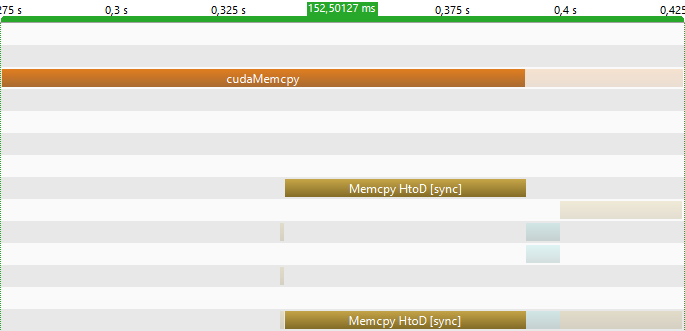
Looking at the Performance its interessting for a 27000x6000 pixel image the calculation takes 0,007 seconds but here is the catch. With nvprof or nvvp we can see that the GPU is only 1,8% of the time busy with computing. The rest is allocation and memory transfer.

Allocation in seconds memcopy HtoD in seconds memcopy DtoH in seconds Kernel in seconds
0.018321 0.054598 0.048913 0.00754453

cuda_profiling

The orange bars are all the called cuda functions like cudamalloc. The blue bar is the kernel activity

There is also a huge overhead from the cudaMemcpy call and the actual Memcpy operation.

Memory on the GPU

The GPU has different kinds of memory. The biggest one is the global memory. Its located on the device Dram. There are other types of memory(like Local memory, constant memory) located on the Dram but we dont need them now. For optimisation is the On Chip memory more interessting especially the Shared Memory. Its very fast so why we didnt used it to make the Kernel function even faster. For this specific task there is no performance gain from using shared memory instead of the global memory because the shared memory doesnt reuse any data so the number of global memory reads stays the same. Also the calculation time only takes arround 2% of the time so maybe its better to focus on the other 98%.

Memorytransfer between GPU and CPU

There is no free lunch In general avoid memory transfer between device and host. Its recommended to to copy the data to the device. Then calculate on the device and then copy the data back.

like in (greyscale.cu)

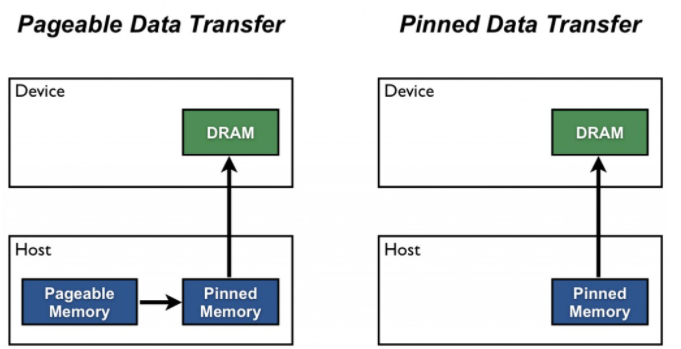
pinned memory

Generaly pinned memory is recommended if we want to overlap copy and compute pinnendMemory https://developer-blogs.nvidia.com/wp-content/uploads/2012/12/pinned-1024x541.jpg

Instead of malloc() we could use cudaMallocHost(). This will allocate the data in the Pinned Memory. I didnt find a way to direclty allocate the Image with the stb_image.h functionality. But luckily CUDA offers cudaHostRegister which will pin memory that is already allocated. instead of allocating host_grey with malloc we use cudaMallocHost which will allocate in the Pinnend Memory.

So the Memory transfer between Host and Device should be faster.

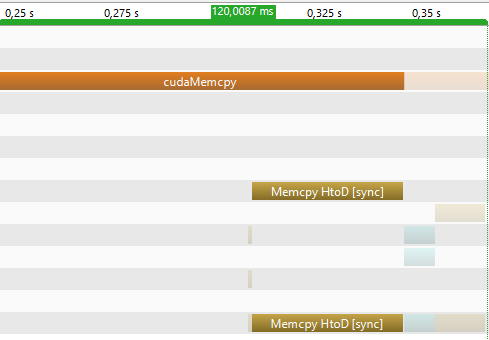
cuda_profiling

well yes and no. The Memcpy HtoD is faster compared to the nonpinnend version(see greyscale.cu). (37 ms vs 55 ms) the cudaMemcpy call still takes (100 ms instead of 120 ms in the nonpinnend version). The Memcpy DtoH is also faster (12 ms v 37 ms) and for the cudaMemcpy call (19,8 ms vs 58 ms)

So we get a minimal transfer speed-up but the Host allocation takes now longer (27 ms)

Allocation in seconds memcopy HtoD in seconds memcopy DtoH in seconds Kernel in seconds
0.292566 0.032401 0.0121894 0.0075523

final runtime with CUDA allocation, memory transfer and kernel execution time in seconds done on a GTX 1060 6GB

greyscale greyscalePinnedMemory greyscaleV2(using pinned memory too)
0.16000 0.16200 0.1100

Possible Solution and idea for future research

It would be interessting to see how a grayscale conversation performs on a M1 with a Unified Memory Architecture. It could be faster since the GPU and CPU using that common pool of memory. There should be no need to transfer the data. The GPU will let the CPU know when its done

CPU

Problem

  • naive solution is single threaded
  • processors can calculate 128/256 bit at once, but only part of it is used in a single iteration
  • data is in rgbrgbrgbrgb format, but rrrrggggbbbb is needed
  • memory is not aligned, meaning that in order to read 8-bytes we may need to actually read 16-bytes

Solution attempt

Multithreaded

The easiest place to optimize it, is utilizing all cores of a CPU and thus convert it to a multithreaded application. This is done with OpenMP by adding the pragma #pragma omp parallel for collapse(2) (see openmp_baseline.c)). omp parallel for parallelizes the for loop with collapse(2) collapsing both loops and thus parallelizing both. This gives a more than 6 times performance boost.

In the next step the memory access can optimized. Currently each thread calculates the grey value for a random pixel, depending on how it is scheduled by openMP. For this it needs to load 3 unsigned char, so 24 bytes from memory. But a CPU preloads more data into the cache anticipating that it will be needed. This behavior can be used to by having each thread operating on a continuous section, thus using the data that is already in the CPU Cache (see memory.c).

SIMD FMA

All references to intrinsic functions can be looked up here: https://www.intel.com/content/www/us/en/docs/intrinsics-guide/index.html

The next place to optimize is utilizing the full register of the CPU by using Single Instruction Multiple Data (SIMD). For example we could add 16 8-bit integers at once in a 128 bit register instead of only a single one, thus theoretically creating a 16 time speedup. Additionally one can use a dedicated arithmetic logic unit that multiplies two numbers and add it to an accumulator, knows as MAC-unit (multiplier-accumulator). This takes the form of "fused multiply add" (FMA), which additionally only rounds at the end, thus combining two operations into one.

The data being in the form of rgbrgbrgbrgb appears for the first time. For FMA a whole register need to be filled with only red, green or blue values, meaning we want the data in rrrrggggbbbb format. This problem is ignored for now, by just setting the register with the appropriate values, which comes with its own performance problems, because with the data being spread out like this, multiple reads may be necessary.

r_vector = _mm_set_ps(img[(i * channels)], img[(i + 1) * channels], img[(i + 2) * channels], img[(i + 3) * channels]);
g_vector = _mm_set_ps(img[(i * channels) + 1], img[(i + 1) * channels + 1], img[(i + 2) * channels + 1], img[(i + 3) * channels + 1]);
b_vector = _mm_set_ps(img[(i * channels) + 2], img[(i + 1) * channels + 2], img[(i + 2) * channels + 2], img[(i + 3) * channels + 2]);

With the data in the correct format the multiplication is very simple

gray_vector = _mm_setzero_ps();
gray_vector = _mm_fmadd_ps(r_vector, r_factor, gray_vector);
gray_vector = _mm_fmadd_ps(g_vector, g_factor, gray_vector);
gray_vector = _mm_fmadd_ps(b_vector, b_factor, gray_vector);

Full code see memory_simd_fma.c

A problem with FMA is, that the basic FMA instruction set only supports working with 32-bit and 64-bit floating point numbers. This means that with a 128-bit register a maximum of 4 pixel can be calculated at once.

SIMD SSE

This implementation if completly copied from a Stackoverflow post by Rotem: https://stackoverflow.com/a/57844027/13516981 Only modification made was making it compatible with pure C, since it was using C++ features (see memory_simd_sse.c)

It has 2 major optimization areas.

First it utilizes shuffle (_mm_shuffle_epi8), concat (_mm_alignr_epi8) and shift (_mm_slli_si128) functions to solve the problem of rearranging the bytes from rgbrgbrgbrgb to rrrrggggbbbb. For example one can group the bytes according to their color like this.

const __m128i shuffle_mask = _mm_set_epi8(9, 6, 3, 0, 11, 8, 5, 2, 10, 7, 4, 1, 9, 6, 3, 0);

__m128i r3_r2_r1_r0_b3_b2_b1_b0_g3_g2_g1_g0_r3_r2_r1_r0 = _mm_shuffle_epi8(r5_b4_g4_r4_b3_g3_r3_b2_g2_r2_b1_g1_r1_b0_g0_r0, shuffle_mask);

Or like this

// The 12 is the amount of bytes to shift the result
__m128i b7_g7_r7_b6_g6_r6_b5_g5_r5_b4_g4_r4 = _mm_alignr_epi8(b7_g7_r7_b6_g6_r6_b5_g5, r5_b4_g4_r4_b3_g3_r3_b2_g2_r2_b1_g1_r1_b0_g0_r0, 12);

If the bytes are not at the start or end in order to concatenate them they are shifted like this

// 8 bytes to the left
__m128i g3_g2_g1_g0_r3_r2_r1_r0_zz_zz_zz_zz_zz_zz_zz_zz = _mm_slli_si128(r3_r2_r1_r0_b3_b2_b1_b0_g3_g2_g1_g0_r3_r2_r1_r0, 8);
// 4 bytes to the right
__m128i zz_zz_zz_zz_r7_r6_r5_r4_b7_b6_b5_b4_g7_g6_g5_g4 = _mm_srli_si128(r7_r6_r5_r4_b7_b6_b5_b4_g7_g6_g5_g4_r7_r6_r5_r4, 4);

Additionally it sacrifices some accuracy by calculating the gray value with 16-bit integers instead of 32-bit floats. But the most important for me is, that it showed me how to work with the bit modification functions in a structured manner by naming the variables according to the bytes it contains.

SIMD AVX

With this knowledge the next step is using the AVX instruction set, which operates on 256-bit registers unlike 128-bit in SSE. This in theory allows one to process twice the amount of pixels at once. Unfortunately many AVX functions behave slightly different compared to their SSE counterpart in the form of only operating within 128-bit lanes instead of across the whole 256-bit register. This means that it is not possible to shuffle a byte from the lower lane to the upper lane with _mm256_shuffle_epi8. So in a register with gA_rA_b9_g9_r9_b8_g8_r8_b7_g7_r7_b6_g6_r6_b5_g5_r5_b4_g4_r4_b3_g3_r3_b2_g2_r2_b1_g1_r1_b0_g0_r0, where the lane split is between g5 and r5, it is not possible to group all red values because r6, r7, r8 and r9 are in the upper lane whereas the other values are in the lower lane.

Because of this for AVX a different set of functions is used in order to group the bytes of each color. The central function is _mm256_blendv_epi8(__m256i a, __m256i b, __m256i mask) which allows to combine parts of the first register with the second one according to the mask.

__m256i g4_g3_g2_g1_g0_b4_b3_b2_b1_b0_r5_r4_r3_r2_r1_r0_b9_b8_b7_b6_b5_rA_r9_r8_r7_r6_r5_r4_r3_r2_r1_r0 =
    _mm256_blendv_epi8(
        g4_g3_g2_g1_g0_b4_b3_b2_b1_b0_r5_r4_r3_r2_r1_r0_b9_b8_b7_b6_b5_rA_r9_r8_r7_r6_gA_g9_g8_g7_g6_g5,
        b9_b8_b7_b6_b5_rA_r9_r8_r7_r6_gA_g9_g8_g7_g6_g5_g4_g3_g2_g1_g0_b4_b3_b2_b1_b0_r5_r4_r3_r2_r1_r0,
        _mm256_set_epi8(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /**/ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 128, 128, 128, 128, 128, 128));

In this example we want to combine the group of red bytes r5_r4_r3_r2_r1_r0 of the second register with the group of rA_r9_r8_r7_r6 in the first one. They are deliberately lined up, so that in the first register before the group of rA_r9_r8_r7_r6 is exactly enough space to fit in the first 6 bytes r5_r4_r3_r2_r1_r0. Accordingly the mask is set to use all values of the first register, except the first 6 ones.

This setup is done through _mm256_shuffle_epi8 with which we can still shuffle inside the lanes in order to group the bytes. Afterwards we can use _mm256_permute2x128_si256(__m256i a, __m256i b, 1) in order to swap the lanes so that we can blend them. In some places _mm256_alignr_epi8 is also used. Like in SSE it concatenates registers, although it only works on 128-bit lanes.

For the exact steps see memory_simd_avx.c where the variable names reflect the outcome of a function.

Another change is aligning the memory of the input and output image. This allows using the aligned load and store functions instead of the unaligned ones (_mm256_load_si256 instead of _mm256_loadu_si256). With this we may avoid loading data that is spread across boundaries of a address and thus reducing memory transfer. The output is aligned with by allocating the memory with aligned_alloc(32, size) instead of malloc(size). For the input image the library used to load the image stb_image.h, allows to override the default malloc function used. We do so be defining following values before the include of that library.

#define STBI_MALLOC(sz)           aligned_alloc(32, size)

Benchmarks

With

Baseline

time in s megapixel per s
2.739997 56.3852

openmp baseline

thread number time in s megapixel per s
12 0.411790 375.1795
32 0.414154 373.0381
64 0.414555 372.6776
128 0.430195 359.1287

memory

thread number time in s megapixel per s
32 0.032053 4820.0608
64 0.031559 4895.3717
128 0.030711 5030.6157
256 0.032755 4716.6270

FMA

thread number time in s megapixel per s
12 0.035387 4365.8509
32 0.035855 4308.9137
64 0.035242 4383.8510
128 0.034176 4520.5836
256 0.035138 4396.8387

SSE

thread number time in s megapixel per s
12 0.030364 5088.0302
32 0.030036 5143.7032
64 0.030248 5107.6352
128 0.030838 5009.9306
256 0.032062 4818.7077

AVX

thread number time in s megapixel per s
12 0.030029 5144.9279
32 0.029775 5188.7483
64 0.030188 5117.7360
128 0.030685 5034.9111
256 0.032302 4782.7716

CPU comparison

CPU algorithm thread number time in s megapixel per s
AMD Ryzen 5 3600 (6 Core) memory 128 0.030711 5030.6157
AMD Ryzen 5 3600 (6 Core) simd_sse 32 0.030036 5143.7032
AMD Ryzen 5 3600 (6 Core) simd_avx 32 0.029775 5188.7483
Intel Core i7-4710HQ (4 Core) memory 128 0.080105 1928.6639
Intel Core i7-4710HQ (4 Core) simd_sse 128 0.056655 2726.9456
Intel Core i7-4710HQ (4 Core) simd_avx 128 0.055232 2797.2128
Intel Core i9-9880H (8 Core) memory 128 0.038570 4005.5441
Intel Core i9-9880H (8 Core) simd_sse 64 0.041884 3688.6061
Intel Core i9-9880H (8 Core) simd_avx 128 0.027279 5663.5644

Review

A review of the AVX variant

Memory Bottleneck

The memory access should not be the bottleneck. There are many indicator for this.

First one being that the Intel Core i9-9880H performs better than the AMD Ryzen 5 3600 even though in has a memory bandwidth of only 39.74 GiB/s compared to 47.68 GiB/s.

Second one being that the alignment of the memory in the AVX step, did not change the performance in any noticeable way. One can test it out by replacing _mm256_load_si256 with _mm256_loadu_si256 and _mm256_store_si256 with _mm256_storeu_si256 and reverting the changes to align the memory.

Lastly doing a calculation of the theoretical amount of transferred data, we are below the available bandwidth.

pixel = 27000*6000 = 162000000
duration = 30ms = 0.03s
pixel_per_iteration = 32
bytes_per_pixel = 3
iterations = pixel / pixel_per_iteration = 5062500
bytes_read_per_iteration = 128 // it is not bytes_per_pixel*pixel_per_iteration=3*32=96, because we are effectively reading so many bytes in this sequence: 32 - 16 - 32 - 16. But because each read is 32-bytes, it results in 4*32=128 bytes read. Because the CPU address width is 8-byte there are no considerations here with 32-byte aligned memory.
bytes_read = bytes_read_per_iteration * iterations = 128 * 5062500  = 648000000
bytes_written = pixel * bytes_per_pixel = 162000000 * 3 = 486000000
bytes_transferred = bytes_read + bytes_written = 648000000 + 486000000 = 1134000000
transfer_rate = bytes_transferred / duration = 1134000000 (byte) / 0.03s = 37800000000 b/s = 35,20 Gb/s

Latency and Throughput

Each SIMD functions has a different latency and throughput. Latency means how many clock cycles it takes for the calculation to be complete and throughput means how much of a clock cycle the operations takes. Taking _mm256_load_si256 as example on the Haswell architecture. It has a latency of 1 and throughput of 0.25. This mean we can load 4 independent datasets in a single clock cycle. This is a source of optimization, that was not done here. It could also be the source of the different benchmark results for the different algorithms between the CPUs. Instead functions were selected purely on being able to arrange the bytes in a way that was needed. The linked intrinsic guide is for Intel, so one for AMD would need to be found first.

Number of Threads

This is something that can be further investigated. Currently they were just discovered through trial and error without putting much thought behind them.

Conclusion

Grayscale conversion is not suited to be computed with the GPU due to transfer 4 bytes of data for each pixel, which are 5 floating point operations in order to convert it to grayscale. The CPU on the other hand is very suited with the easiest performance improvement being to parallelize it and grouping the memory access. This can be easily done because each calculation is independent from another one. SIMD can be used to further improve it, but only in the very smallest margins at the cost of huge developer overhead.