Cross entropy or Hinge loss
tell you how many bits you need to tranmit the messeges
p: actual probability
q: predicted probability
when p = q, the cross entropy has its minimum. It penalize the prediction that is highly confident but inaccurate.
For example, if one example belong to class 1, then the actually probability of class one is 1, class two is 0, then the cross entropy will be -1log(1)+-0log(0) log(1) is zero and log(0) is -Inf, therefore, the cross entropy is 0
but on the other hand, if the classifier predict it is clas two while the true label is class one the cross entropy will be Inf
def cross_entropy(X,y):
"""
X is the output from fully connect layer (shape with n_example, n_classes)
y is labels (n_example, 1)
"""
m = y.shape[0]
p = softmax(X)
log_likelihood = -np.log(p[range(m), y])
loss = np.sum(log_likelihood)/m
return loss
For unbalanced classes, can use Focal Loss:
In simplified terms, it is a measure of the distrance of two distributions. One appication of KL divergence is the famous generative adversarial network (GAN). KL divergence from distribution Q to P:
From above, you can see that KL divergence = Entropy - Cross Entropy When the Entropy is constant, we only need to minimize the cross entropy in order to maxified the KL divergence. Why do we want a large KL divergence? When the difference is large, it is easier to seperate the two classes!
KL divergence is not symmetric, meaning, D(P||Q) is not equal to D(Q||P).
Example: KL Divergence in this example can be understand as the number of extra bits needed in avarage to transmit a value drawn from distribution P when we use a code that was designed for another distribution Q? Note that in this example, the frequence was set as 1/2 or 1/4. In reality, it doesn't need to be two to the power of n, which means the KL divergence is the lower bound of the extra average length to transmit data. When P is the same as Q, then obviously, this increase is 0.
Mutual information using KL-divergence: I(X;Y)=KL(p(x,y)||p(x)p(y)), x and y are two indepedent variables. Minimizing mutual information is equal to maximizing the KL-divergence.
Hinge loss all penalize those that are correct but not confident
Hinge loss is faster to train in gradient descent than cross entropy - real time desicion making
If accuracy is more important, use cross entropy
MSE, MAE or Huber loss
MAE (L1 loss), is more robust to outliers than MSE
Huber loss, even more robust to outliers
1.Gradient descent family
(1) fixed learning rate
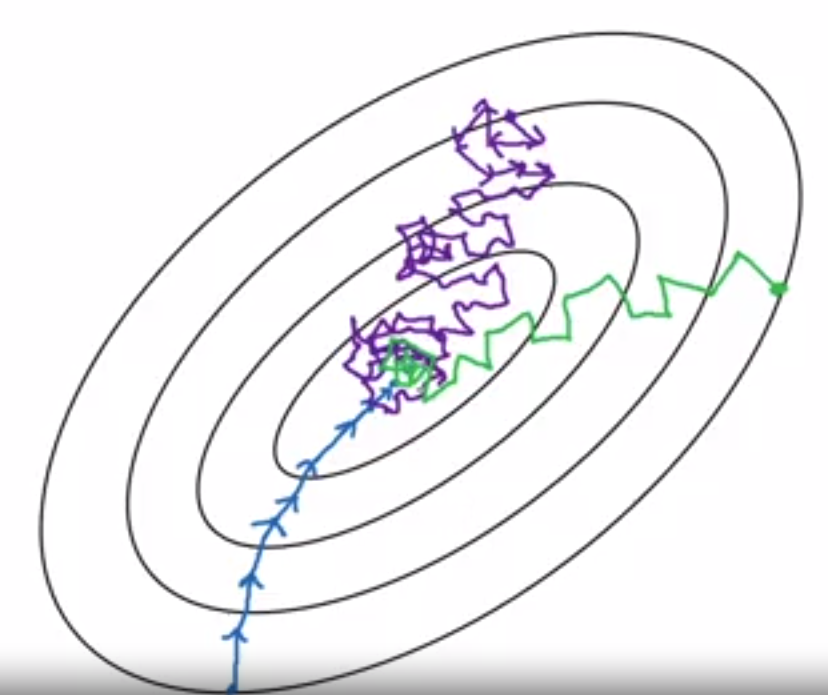
a. Blue: Batch gradient descent (vanilla) - update the whole training example in one iteration. It can take a long time for one iteration. When less than 2000 examples, use a.
b. Purple: Stochastic gradient descent - update one training example in one iteration. It can be slow due to the loss of the advantage of vectorization.
c. Green: Minibatch gradient descent - update one batch/ several examples in one iteration/epoch, it runs much faster than a. for a large dataset. Tips: when choosing the batch size, 2^n usually have been computational efficiency. It is the most commonly used among the three. Typical values of the batch size: 64, 128, 256 and 512. Make sure one batch fits into the GPU memorgy.
(2) adaptive learning rate
Before going into details, we need to first understand two concepts: exponentially weighted averages and bias correction.
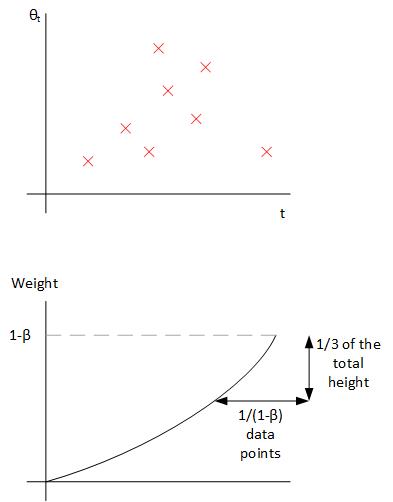
a. The exponentially weighted averages can be understand as the average of the original data (upper graph) multiplied by the weight (lower graph).
The exponentially weighted average: , where
is the calculated average at time point t, and
is the original data at time point t. The exponentially weighted average method can be understood as taking the average of the last
. For example, when
, it can be understand as averaging the last 20 data points. When
, it can be understand as averaging everying 50 timesteps.
The above means that for V100, the contribution of theta(100-9) is only 1/3 as the contribution fo theta(100).
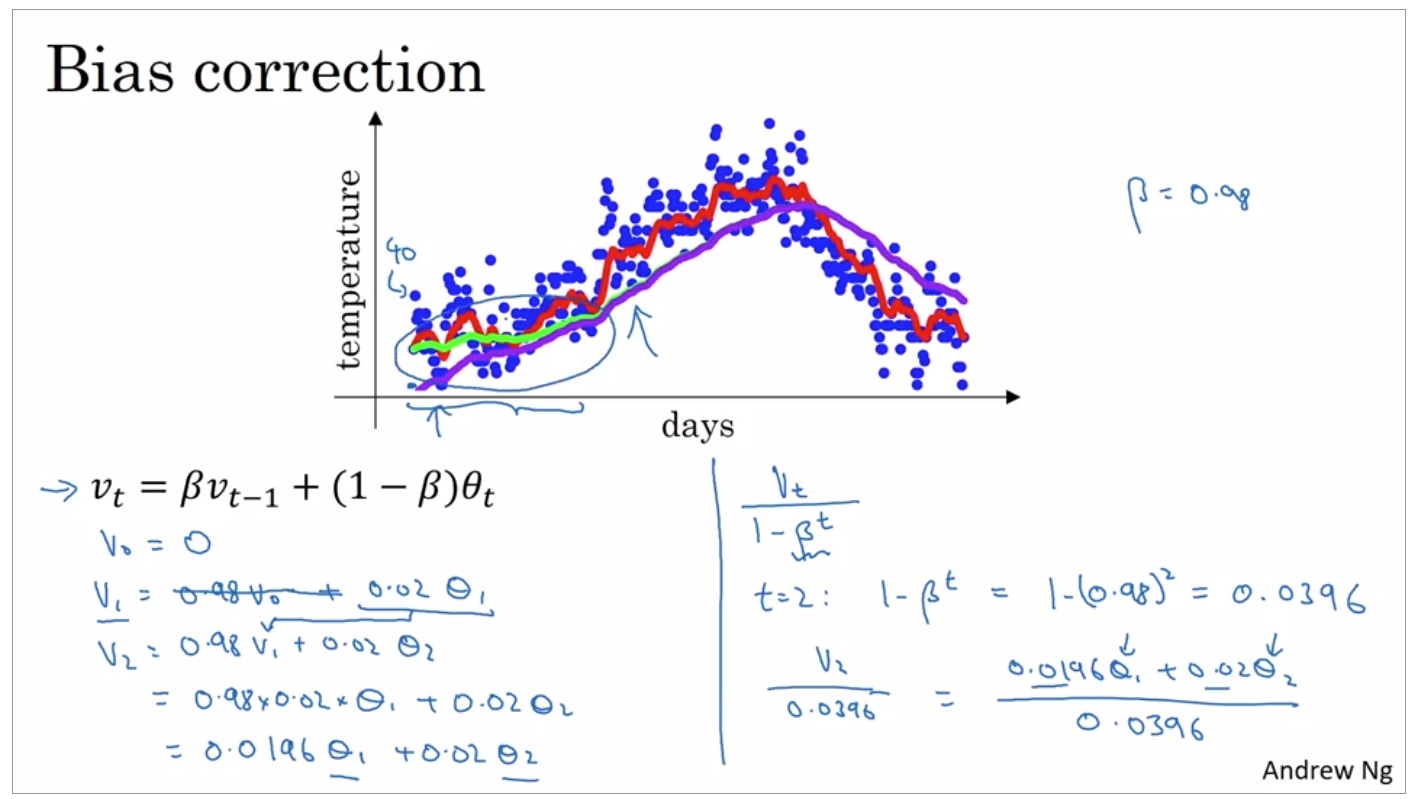
b. Bias correction In exponentially eighted average, we have the first average point V0 = 0, that means that at the beginining of the averaging point, the averaged is lower than what is ideal. As in the below group, instead of getting the green curve, we get the purple curve. Bias correction is a method to correct this effect. However, in DL, bias correction is not always applied as we may only care the later values but not the initial values. (The red curve is by conventional averaging method).
- Gradient descent with momentum
Applying the weighted decay averaging concept into the weight update in NN training, we have:
-
LeNet: Use conV net (shared weight)
-
AlexNet: ReLU, dropout, Data augmentation
-
VGG-16/19 Stage-wise training - requried Xavier/MSRA initation
-
GoogleNet Multiple branches, shortcuts, bottleneck
Use Batch Norm
- ImageNet Deep residual learning 1x1 conv has lower time complexity than VGG-16/19