SimPL-Interpreter

Ziteng Yang

1. Overview

This is the implementation document of an interpreter for the programming language SimPL (pronounced simple), which is a simplified dialect of ML and can be used for both functional and imperative programming.

See project.pdf for the specification of this language and the original goals.

The project has been uploaded to https://github.com/Youngzt998/SimPL-Interpreter

2. Project Architecture

2.1. Files Structure

2.1.1. Source code

The entry of the main Java class was in src/simpl/interpreter/Interpreter.java. Besides, other code files are listed:

src/simpl/parser/: the parser generator and parser used in this project for SimPL
- ./ast/*.java: Classes representing the abstract syntax tree for SimPL
src/simpl/interpreter/
- ./*Value.java : The value class and all its subclass, used for evaluation steps
- ./lib and ../pcf: Several predefined functions
- State.java, Env.java, ... : Classes representing the environment of a SimPL program evaluation
src/simpl/typing/*.java: Classes representing the types of SimPL

2.2.2. Other Files

Readme.md : this file
project.pdf: a specification of SimPL, i.e. the original goal of this project
structure.pptx: a graphic structure showing the sub-tying relations among all Java classes

2.2. Test the Interpreter

A packaged .jar file was uploaded to the examples file, i.e. ./examples/SimPL.jar. There are also some SimPL program. See factorial.spl as an example:

let fact = rec f => fn x => if x=1 then 1 else x * (f (x-1))
in  fact 4
end
(* ==> 24 *)

To test the interpreter, open the terminal in this file and run the following code in command line (Java environment was required):

java -jar ./SimPL.jar ./factorial.spl

If every thing goes right, we will get the output:

int
24

3. Implementation Details

3.1. Principle Data Structures

3.1.1. Symbols and Expressions

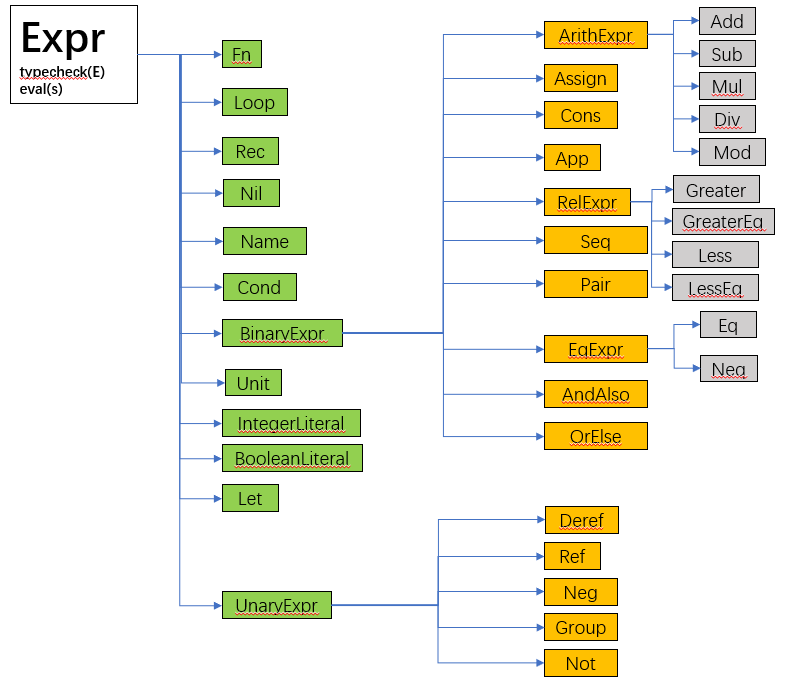
Any valid program of SimPL would be parsed into a Java abstract class Expr [defined in src/simpl/parser/ast/Expr.java], which has several subtype, defined as follows:

public abstract class Expr {

    public abstract Expr replace(Symbol x, Expr e);
    public abstract TypeResult typecheck(TypeEnv E) throws TypeError;
    public abstract Value eval(State s) throws RuntimeError;
}

Three member function are declared:

replace: Replace a variable x in this expression with another express e
typecheck: Check the type of this expression and throw TypeError if it has type error.
eval: Evaluate the expression following the operational semantics in the Specification

A Symbol x can be considered as a variable expression, but it should be encapsulated in Name(x) as an expression.

The next figure suggest the sub-typing structures of all expressions:

3.2. Abstract Syntax Tree (AST)

3.2.1. Arithmetic and Boolean Expressions

We use Add (arithmetic) and Not (boolean) expression as examples.

Add expression was inherited from ArithExpr expression that implements several common features of arithmetic expressions. Again ArithExpr was inherited from binary expression BinaryExpr.

In Java, it can be implemented as the following (eval method was left in evaluation part):

public abstract class BinaryExpr extends Expr {

    public Expr l, r;
    public BinaryExpr(Expr l, Expr r) {
        this.l = l;
        this.r = r;
    }
}

which states that a binary expression consists of two expressions, and

public abstract class ArithExpr extends BinaryExpr {

    public ArithExpr(Expr l, Expr r) {
        super(l, r);
    }
    
    @Override
    public TypeResult typecheck(TypeEnv E) throws TypeError {
    	...
    }
}

that defines the same typing rule of all arithmetic expressions, and

public class Add extends ArithExpr {

    public Add(Expr l, Expr r) {
        super(l, r);
    }

    public String toString() {
        return "(" + l + " + " + r + ")";
    }

    @Override
    public Add replace(Symbol x, Expr e) {
        return new Add(l.replace(x, e), r.replace(x, e));
    }

    @Override
    public Value eval(State s) throws RuntimeError {
		...
    }
}

that defines the specific evaluation rules of Add.

The replace method was defined recursively.

Not expression is similar to Add , but it was inherited from UnaryExpr:

public class Not extends UnaryExpr {

    public Not(Expr e) {
        super(e);
    }

    public String toString() {
        return "(not " + e + ")";
    }

    public Not replace(Symbol x, Expr e) {
        return new Not(this.e.replace(x, e));
    }


    @Override
    public TypeResult typecheck(TypeEnv E) throws TypeError {
		...
    }

    @Override
    public Value eval(State s) throws RuntimeError {
		...
    }
}

3.2.2. Lambda Calculus and Functional Application

The Lambda calculus in SimPL was denoted by fn x => e

In Java implementation, it consist of a Symbol x and an Expr e:

public class Fn extends Expr {

    public Symbol x;
    public Expr e;
 
    /* specific method for Fn */
    ...
}

Note that the replace interface should compare this.x with x:

@Override
public Fn replace(Symbol x, Expr e) {
    if(this.x.toString().equals(x.toString())){
        return this;
    }
    else return new Fn(this.x, this.e.replace(x, e));
}

The functional application $e_1\ e_2$ was just a binary expression.

3.2.3. Let Expressions

The Let expression $let\ x = e_1\ in\ e_2$ also has a Symbol member representing the variable x

public class Let extends Expr {

    public Symbol x;
    public Expr e1, e2;
    /* specific method for Let */
    ...
}

3.2.4. List, Pair and Other Structures

The SimPL language also has some structures such as list and pair. The list was named Cons and the pair was Pair. The Java class of them are similar to the previous ones.

3.2.5. Imperative Features

SimPL also has imperative features such as while-loop, assignment and (virtual) memory location.

Loop was the while-loop $while\ e_1\ do\ e_2$ of SimPL.
Ref represents a unary operation $ref\ e$ denoting a memory reference to $e$ ; correspondingly, Deref represents a unary operation $!e$ that aim to get the value from the memory reference.
Assign represent an assignment $e_1\ :=\ e_2$ that change the value of the memory referred by $e_1$

All the Java classes' structure of the above expressions are similar to the previous ones, varying in their members as well as the replace, typecheck and eval method.

3.3. Type Checking with Polymorphism

[ Note: Although for the interpreter, type checking runs first, it might give a better understanding about the code to see evaluation step first. ]

Before running the program, we should do a type checking first to avoid some runtime error.

3.3.1. The Class Type

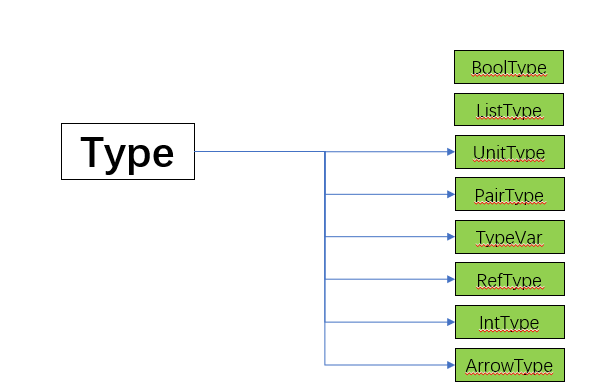
An abstract class Type was defined representing the data type of SimPL:

public abstract class Type {

    public abstract boolean isEqualityType();
    public abstract Type replace(TypeVar a, Type t);
    public abstract boolean contains(TypeVar tv);
    public abstract Substitution unify(Type t) throws TypeError;

    public static final Type INT = new IntType();
    public static final Type BOOL = new BoolType();
    public static final Type UNIT = new UnitType();
}

isEqualityType decide whether this type was comparable (such as $e_1 = e_2$)
replace change all occurrence of a type variable a in this type to some typet`
contains checks whether this type contains the type variable tv
unify gives a Substitutino structure stating that this type is equal to the type t, which would be used in the unification process

The following figure shows the sub-type relation of Type

3.3.2. The Class Substitution and Unification Algorithm

The Substitucion was a data structure that implements the unification algorithm in type inference.

It has a method apply, that transform one type to another type, i.e. $S(a) = t$ in unification process.

public abstract class Substitution {
    public abstract Type apply(Type t);
    /* Some methods and subtypes */
    ...
}

It has three subtype

Identity: the identity function, which means "do nothing": give the t, return the t

private static final class Identity extends Substitution {
    public Type apply(Type t) {
        return t;
    }

    public String toString(){
        return "Id";
    }
}

Replace: the single substitution $[a=t]$

private static final class Replace extends Substitution {
    private TypeVar a;
    private Type t;

    public Type apply(Type b) {
        return b.replace(a, t);
    }

    public String toString(){
        return a + " = " + t;
    }
}

Compose: the composition of two substitution $T * S(a)= T(S(a)) $

private static final class Compose extends Substitution {
    private Substitution f, g;

	...
    public Type apply(Type t) {
        /**
        *  The sequence is principle
        */
        return g.apply(f.apply(t));
    }
	...
}

3.3.2. Type Checking and Inference

The SimPL uses implicit type, and also has polymorphic types. Type inference was achieved, including Let-Polymorphism. Following cases of type checking for normal expressions and let expressions was used to suggest how to implement type inference by unification.

Arithmetic Expressions

The interface typecheck generates the implementation:

Expr l, r;
...
@Override
public TypeResult typecheck(TypeEnv E) throws TypeError {
	...    
}

Now we have expression l and r,, and current type environment E. We want to check whether l + r was a valid expression. The first thing is to check l under E:

TypeResult tr1 = l.typecheck(E);

A TypeResult consists of a Substitution s and a Type t. An principle issue is that, this might give new type environment, so we must check r in the new environment:

TypeEnv NewE = tr1.s.compose(E);
TypeResult tr2 = r.typecheck(NewE);

Now we have two result and two substitution. According to the constraint typing rule

/*
*  Compose two substitution to get a new substitution
*      then compose two substitution that {tr1.t = Int} and {tr2.t = Int}
*
*      G |- e1: t1, q1    G |- e2:t2, q2    bop \in {+, -, *, /}
*      ------------------------------------------------------------
*      G |- e1 bop e2: int, q1 U q2 U {t1 = int} U {t2 = int}
*/

we should give a new substitution composed by

the ones from l, r and
the hint l and r 's type should be INT

Substitution comp = tr1.s.compose(tr2.s);
Substitution s1 = comp.apply(tr1.t).unify(Type.INT);
comp = comp.compose(s1);
Substitution s2 = comp.apply(tr2.t).unify(Type.INT);
comp = comp.compose(s2);

return TypeResult.of(comp, Type.INT);

A crucial issue here is that comp.apply(tr1.t) would transform the last type result tr1.t to a more specific type $S(tr1.s)$ . This indeed realize the unification algorithm, without specially run it seperately.

Functional Application

For the function $fn.x => e_1$, it introduces a new variable x, but we do not know the type of it. So we create a new TypeVar variable to join the type inference.

TypeVar a = new TypeVar(true);

But we can still check the type of $e$, additionally with the assumption $[x: a]$ added to current environment.

TypeResult tr = e.typecheck(TypeEnv.of(E, x, a));

We should know the type of this expression is some ArrowType, so we return a new ArrowType with the substitution, yet we might not get the full information of $e$ 's type.

ArrowType arrow = new ArrowType(tr.s.apply(a), tr.s.apply(tr.t));
return TypeResult.of(tr.s, arrow);

Name

Name is an expression corresponding to the single variable expression. To check the type of a variable, we could do nothing more but refer to current type environment. If current variable was not bound to any type, then we found a type error.

@Override
public TypeResult typecheck(TypeEnv E) throws TypeError {
    // TODO
    if (E.get(x) == null)
        throw new TypeError("type error: symbol " + x + "not found");

    return TypeResult.of(E.get(x));
}

Let and Let-Polymorphysm

Most of the implementation are similar to the ones above by following the constraint typing rules, except Let since we wish to realize Let-Polymorphism by rule

/**
*  Rule CT-LETPOLY:
*      G |- e2[e1/x]: t2, q   G|- e1: t1
*      ---------------------------------
*      G |- let x = e1 in e2 end: t2, q
*/

which suggests us to replace x with e1 in e2 first and then do type checking instead of check e1 directly.

We still should run the typecheck

e1.typecheck(E);

because we do not wish $let\ x\ =\ <type\ error\ expr>\ in\ 1$ to pass the checking.

Then we can do the replacement and give the result:

TypeResult tr = e2.replace(x, e1).typecheck(E);
return TypeResult.of(tr.s, tr.s.apply(tr.t));

3.4. Evaluation

After type checking, the program should run normally and it's time to evaluate the it.

3.4.1. The Class Value

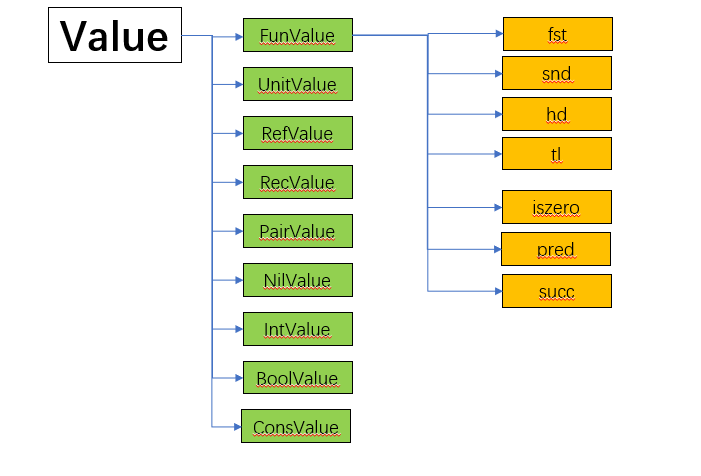
We use the class Value to represent the final value

public abstract class Value {
    public static final Value NIL = new NilValue();
    public static final Value UNIT = new UnitValue();

    public abstract boolean equals(Object other);
}

The member of Value was very simple with a method equals to check the equality.

The following figure shows the sub-type relation of Value

3.4.2 Evaluate the Expression

The implementation of evaluation was shown by the following representative examples.

Arithmetic Expression

Again the Add was used as an example, now we implement the eval interface in Add to realize this evaluation step under $e_1 + e_2$

@Override
public Value eval(State s) throws RuntimeError {
    // TODO
    /*
            Check Type ?
            Or type already checked here?
        */
    return new IntValue(((IntValue)l.eval(s)).n + ((IntValue)r.eval(s)).n);
}

The evaluation was taken recursively (using Big-step Semantics) : just evaluate the left and the right, then add them together.

Functional Application

In Lambda Calculus, the function $fn\ x=>e$ was just a value. So we just give a FunValue for the evaluation of Fn

public Symbol x;
public Expr e;
...
public Value eval(State s) throws RuntimeError {
    // TODO
    /**
         *  Just evaluate to a FunValue
         */
    return new FunValue(s.E, x, e);
}

Then we can implement the application $e_1\ e_2$ method App .

Firstly we know l must evaluate to a FunValue since it past the type check, then we evaluate r to a Value v2. Now the expression in the FunValue should replace its x with Value v2

public Expr l, r;
@Override
public Value eval(State s) throws RuntimeError {
    FunValue v1 = (FunValue) l.eval(s);
    Value v2 = r.eval(s);
    return v1.e.eval(State.of(new Env(v1.E, v1.x, v2), s.M, s.p));

}

Let Expression

The Let expression's evaluation step was very simple: evaluate the e1 to v1, then replace x in e2 by v1, while we do not replace it directly but update current environment instead to save computation and avoid renaming issues.

Value v1 = e1.eval(s);
return e2.eval(State.of(new Env(s.E, x, v1), s.M, s.p));

Imperative Expressions

If a Ref expression was evaluate, then a new memory unit was created, so the memory pointer should increase. After evaluation, the value of this expression should be stored in memory.

public Expr e;
...
@Override
public Value eval(State s) throws RuntimeError {
    int i = s.p.get();
    s.p.set(i + 1);
    Value v = e.eval(s);
    s.M.put(i + 1, v);
    return new RefValue(i + 1);
}

And if we want to get the memory content by Deref, we just get the memory pointer of v evaluated from e and search the (virtual) memory unit.

public Expr e;
...
@Override
public Value eval(State s) throws RuntimeError {
    // TODO
    /**
         *  e -> v where v = (ref vp)
         *  !e -> M(vp) where s = (E, M, p)
         */
    RefValue v = (RefValue) e.eval(s);
    return s.M.get(v.p);
}

3.5. Built-in Funtion

See fst as an example: it was a FunValue, and has a symble fst , and a special expression that return the first element of a variable named fst in current environment.

public class fst extends FunValue {

    public fst() {
        super(Env.empty, Symbol.symbol("fst"), getExpr());
    }

    private static Expr getExpr(){
        Expr e = new Expr() {
            @Override
            public Expr replace(Symbol x, Expr e) {
                return this;
            }

            @Override
            public TypeResult typecheck(TypeEnv E) throws TypeError {
                return TypeResult.of(new TypeVar(true));
            }

            @Override
            public Value eval(State s) throws RuntimeError {
                PairValue v =(PairValue) s.E.get(Symbol.symbol("fst"));
                return v.v1;
            }
        };
        return e;
    }

}