/fairness-in-credit-scoring

Primary LanguageJupyter Notebook

Explore Influence of Imbalance Dataset on Fairness

Measuring Potential Discrimination

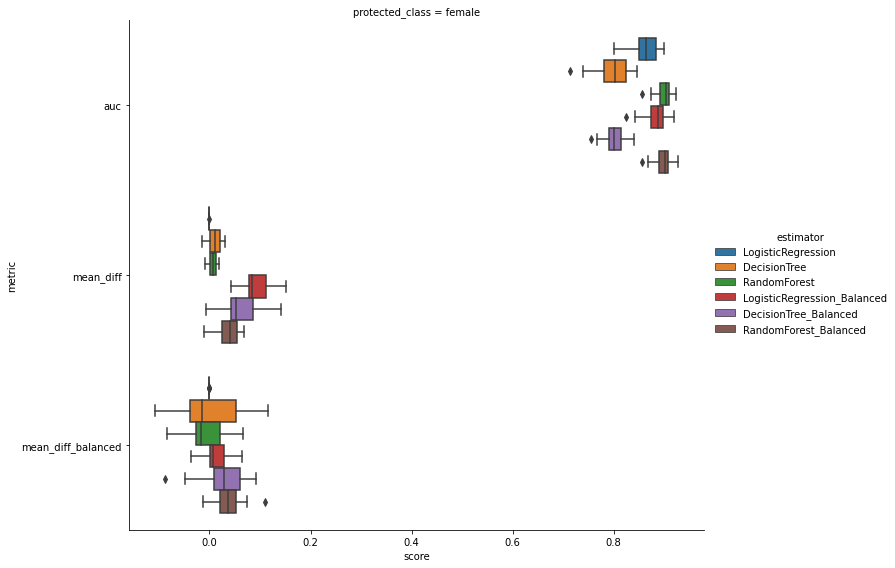
Firstly, we use mean difference as our measure of potential discrimination with respect to a binary target variable credit risk and two protected classes sex .

This metric belongs to a class of group-level discrimination measures that captures differences in outcome between populations, e.g. female vs. male . And we compute this metric on the original dataset.

Mean Difference: 1.46 - 95% CI [-0.03, 2.94]
Normalised Mean Difference: 1.88 - 95% CI [0.39, 3.37]

Below we use StratifiedKFold for 5-fold validation so that we can partition our data according to the protected class of interest and train the the following models:

  1. LogisticRegression

  2. DecisionTreeClassifier

  3. RandomForestClassifier

  4. LogisticRegression_Balanced

  5. DecisionTreeClassifier_Balanced

  6. RandomForestClassifier_Balanced

    LOGISTIC_REGRESSION = LogisticRegression(
    penalty="l2", C=0.001)
DECISION_TREE_CLF = DecisionTreeClassifier(
    criterion="entropy", max_depth=10, min_samples_leaf=10, max_features=10)
RANDOM_FOREST_CLF = RandomForestClassifier(
    criterion="entropy", n_estimators=50, max_depth=10, max_features=10,
    min_samples_leaf=10)

LOGISTIC_REGRESSION_Balanced = LogisticRegression(
    penalty="l2", C=0.001, class_weight="balanced")
DECISION_TREE_CLF_Balanced = DecisionTreeClassifier(
    criterion="entropy", max_depth=10, min_samples_leaf=10, max_features=10,
    class_weight="balanced")
RANDOM_FOREST_CLF_Balanced = RandomForestClassifier(
    criterion="entropy", n_estimators=50, max_depth=10, max_features=10,
    min_samples_leaf=10, class_weight="balanced")
    
estimators = [
        ("LogisticRegression", LOGISTIC_REGRESSION),
    ("DecisionTree", DECISION_TREE_CLF),
    ("RandomForest", RANDOM_FOREST_CLF),
    ("LogisticRegression_Balanced", LOGISTIC_REGRESSION_Balanced),
    ("DecisionTree_Balanced", DECISION_TREE_CLF_Balanced),
    ("RandomForest_Balanced", RANDOM_FOREST_CLF_Balanced)
]

Note that we construct balanced version of three models, i.e., LogisticRegression, DecisionTree and RandomForest, with a default parameter class_weight. For how class_weight works: It penalises mistakes in samples of class[i] with class_weight[i] instead of 1. For instance, given a 0-1 binary classification problem, we have a loss function loss = 0.5*[loss|Y=0]+0.5*[loss|Y=1]. If we set class_weight={ 0:0.8, 1:0.2 } # assume 200 samples with label 0, and 800 samples with label 1, the loss function will be loss = 0.5*0.8*[loss|Y=0]+0.5*0.2*[loss|Y=1].

We set class_weight="auto" or "balanced" , which is equivalent to simply assigning weight[0] = w0 = 2*N1/(N0+N1) and weight[1] = w1 = 2*N0/(N0+N1), where there are N0 data points belonging to class 0 and N1 data points belonging to class 1.

Preliminary results

Obviously, there are some preliminary results with class_weight in a most straightforward and rude way, and then, more sophisticated techniques for weighting in a sample level instead of class level will be implemented and validated.

1. Construct models using all attributes

Training models:
-----------------------------------------
LogisticRegression, fold: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

DecisionTree, fold: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

RandomForest, fold: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

LogisticRegression_Balanced, fold: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

DecisionTree_Balanced, fold: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

RandomForest_Balanced, fold: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
estimator auc mean_diff mean_diff_Balanced
DecisionTree 0.798433 0.018205 0.019376
DecisionTree_Balanced 0.800543 0.051310 0.021330
LogisticRegression 0.862700 -0.000016 -0.000327
LogisticRegression_Balanced 0.885321 0.091049 0.013597
RandomForest 0.899339 0.004725 0.007566
RandomForest_Balanced 0.901759 0.040864 0.028137

allvariable