MeshGPT

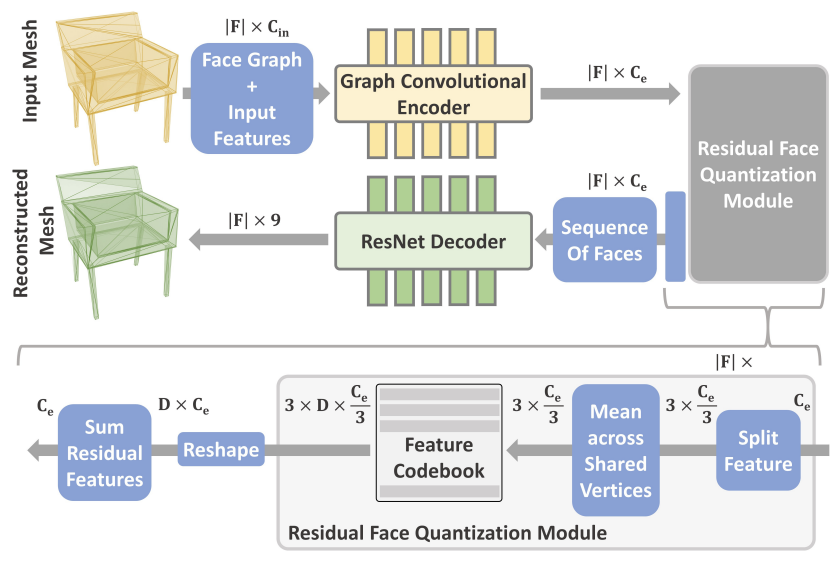
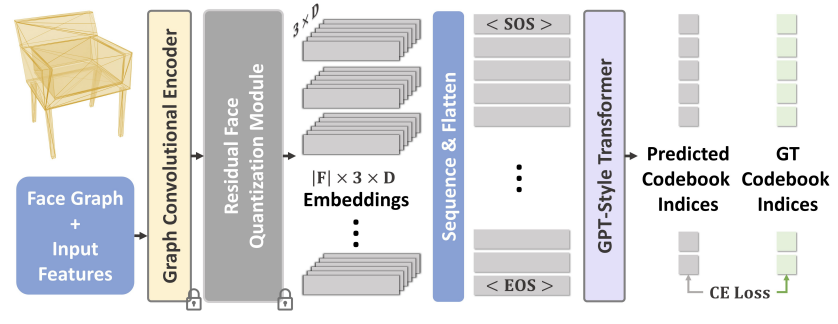
Pytorch Implementation of MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers

Dependencies

Requirements:

wget http://shapenet.cs.stanford.edu/shapenet/obj-zip/ShapeNetCore.v2.zip

Dataset
- ShapeNetV2, 55 categories.
- Trained on all 55 categories, finetuned on Chair, Table, Bench, Lamp
- Preprocess
  - Planar Decimation (Blender)
    - angle tolerance $\alpha \in [1,60]$
    - Hansdorff distance closest and below $\delta_{hansdorff}$
  - Filter
    - face num $\leq$ 800
    - resulting in 28980 in data size
  - Train Test Split
    - Chair, Table, Bench, Lamp 9:1
  - Normalization
    - centered at origin
    - longest side = 1
  - Augmentation
    - Scaling [0.75, 1.25] at each axis, keep longest side = 1
    - Jitter shift [-0.1, 0.1]
    - Planar Decimation (PolyGen), varying levels, keep below $\delta_{hansdorff}$
Model
- Codebook
  - Sequence ordering (PolyGen)
  - Face feature $f_i$
    - face = ${(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)}$
    - 9 coordinates (positonal embedded)
    - area
    - angles between its edges
    - face normal
  - Mesh $\mathcal{M} = (f_1,f_2,...,f_N)$
  - Encoder E (a stack of SAGEConv Encoders)
    - $Z = E(\mathcal{}M)$
  - Quantization (RQ)
    - D=6 codes per face, each vertex D/3 code, 3 vertex
    - mean pooling vertex, concatenate face
    - $T = RQ(Z)$
    - Stochastic Sampling, Exponential moving average
  - Decoder G (1D ResNet34)
    - $\mathcal{M} = G(Z)$
    - classification of 128
- GPT
Training
- Encoder-Decoder: 2 A100 2 days
- GPT2: 4 A100 5days
- Adam, LR=$10^{-4}$, BATCHSIZE=64