This book will be published jointly by Springer Nature and Tsinghua University Press. It will be printed probably in the second half of 2023.
I have received some comments and suggestions about this book from some readers. Thanks a lot and I appreciate it. I am still collecting feedback and will probably revise the draft in several months. Your feedback can make this book more helpful for other readers!
The lecture slides have been uploaded in the folder "Lecture slides".
The lecture videos (in Chinese) are online. Please check our Bilibili channel https://space.bilibili.com/2044042934 or the Youtube channel https://www.youtube.com/channel/UCztGtS5YYiNv8x3pj9hLVgg/playlists
The lecture notes and lecture videos are not complete yet. We will keep updating the videos and slides. Please stay tuned.
This is a draft of a new book entitled “Mathematical Foundations of Reinforcement Learning.” While there already exist many excellent studying materials about reinforcement learning (RL), why do I write a new book?
I have been teaching a graduate-level course on RL for four years. Along with the teaching, I have been preparing this book as the lecture notes for my students. The main reason for me to write this book and develop this course is that I personally think the existing studying materials for RL are either too intuitive or too mathematical.
There are many excellent studying materials that introduce RL topics in intuitive ways. In these materials, the mathematics behind these topics is kept to a minimal level to adapt for a broader readership. Intuitive introductions are good in the sense that readers can grasp the ideas of a topic quickly. However, if the readers would like to understand a topic better, they have to dig out the mathematics that is scattered in technical papers and other materials, which is a huge barrier to their study. On the other hand, there are also many excellent mathematical introductions to RL. These materials, however, usually involve intense mathematics and may require the readers to have professional background on, for example, control theories.
This book aims to provide a mathematical but friendly introduction to the fundamental concepts, basic problems, and classical algorithms in RL. Some important features of this book are highlighted as follows.
- The book introduces RL topics from a mathematical point of view in the hope that readers can better understand the mathematical root of an algorithm and hence why this algorithm is designed in the first place and why it works.
- The depth of the mathematics is carefully controlled to an adequate level. The ways that the mathematics is presented are also carefully designed to ensure the book is friendly to read.
- Many illustrative examples are given to help the readers better understand the topics. All the examples in this book are based on the grid-world task, which is very easy to understand and helpful in illustrating new concepts and algorithms.
- When introducing an algorithm, the book aims to separate its core idea from the complications that may distract the readers. In this way, I hope that the readers can better grasp the core idea of an algorithm.
- This book includes a Q&A section at the end of each chapter. This is motivated by the frequently asked questions on the Internet. I also sometimes contribute to answering some questions online. Although the answers to many frequently asked questions can be found in the main text of the book, they may not be easy to find. Therefore, I believe it is beneficial to list these questions and answers explicitly.
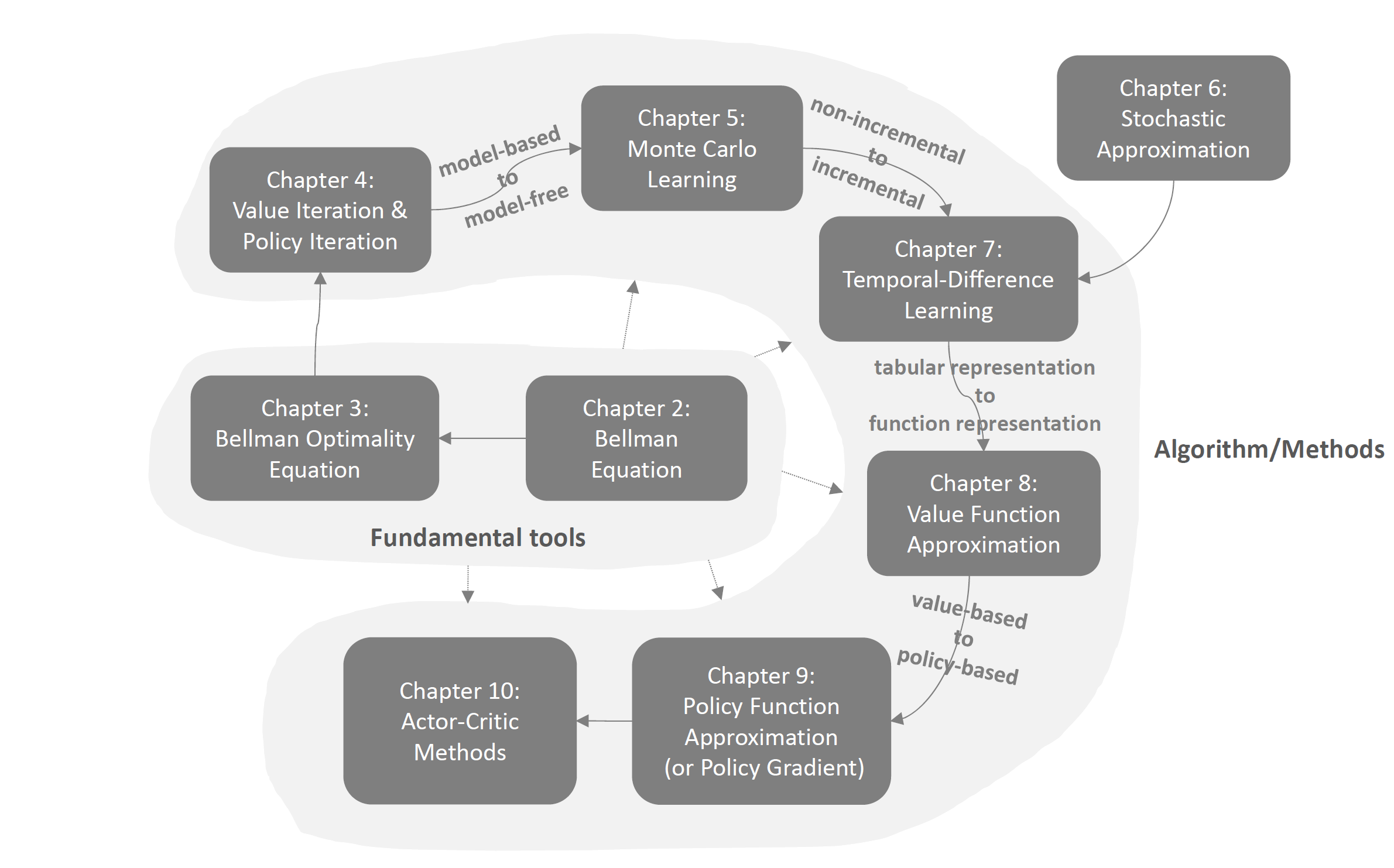
- The contents of the book are organized coherently. Each chapter is built based on the preceding chapter and lays a necessary foundation for the consequent chapters. The relationship between the contents of different chapters is shown below.
Here is a brief description of the relationship between the chapters in this book. Chapter 2 introduces the Bellman equation, which is a fundamental tool for analyzing state values. Chapter 3 introduces the Bellman optimality equation, which is a special Bellman equation. Chapter 4 introduces the value iteration algorithm, which is an algorithm solving the Bellman optimality equation. Chapter 5 introduces Monte Carlo learning, which is an extension of the policy iteration algorithm introduced in Chapter 4. Chapter 6 introduces the basics of stochastic approximation, which lays a foundation for introducing temporal-difference learning in Chapter 7. Chapter 8 extends the tabular temporal-difference learning methods to the case of value function approximation. While Chapter 9 switches to policy iteration, Chapter 10 introduces actor-critic methods, which are a combination of the contents in Chapter 8 and Chapter 9.
This book is aimed at senior undergraduate students, graduate students, researchers, and practitioners who are interested in RL.
It does NOT require the readers have any background on RL because it starts by introducing the very basic concepts of RL. However, if the readers already have some background in RL, I believe the book can also help them to understand some topics deeper or provide them with different perspectives.
This book, however, requires the readers to have some knowledge of probability theory and linear algebra. Some basics of the required mathematics are also included in the appendix of this book.
This book has not been finalized yet. A few more chapters will be added. The slides and videos for my course will also be uploaded online. The publisher of this book will be announced.
I am collecting feedback about this book. Any feedback will be appreciated. Please send feedback to zhaoshiyu[-at-]westlake.edu.cn.
You can find my info on my homepage https://www.shiyuzhao.net/ (GoogleSite) and my research group website https://shiyuzhao.westlake.edu.cn