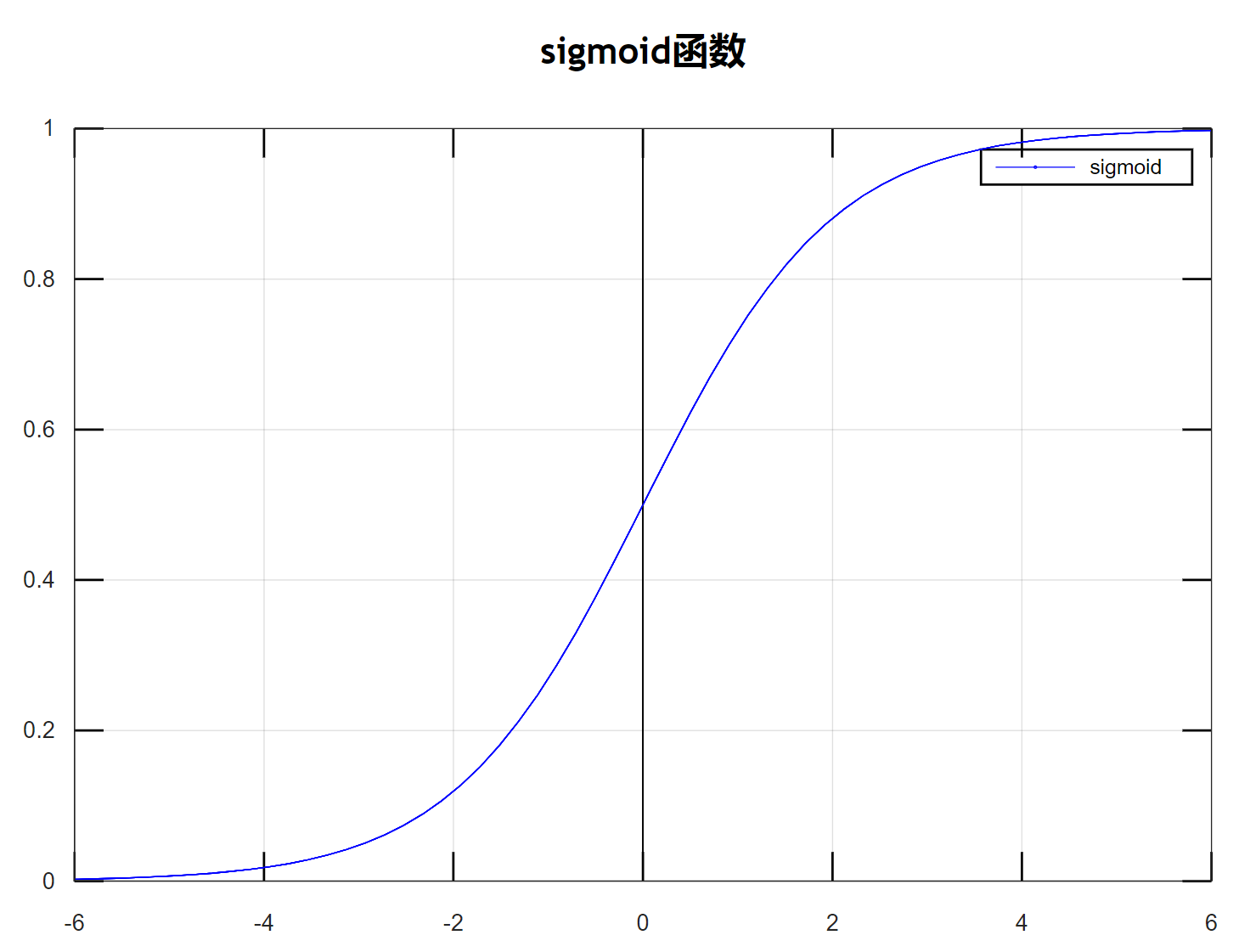
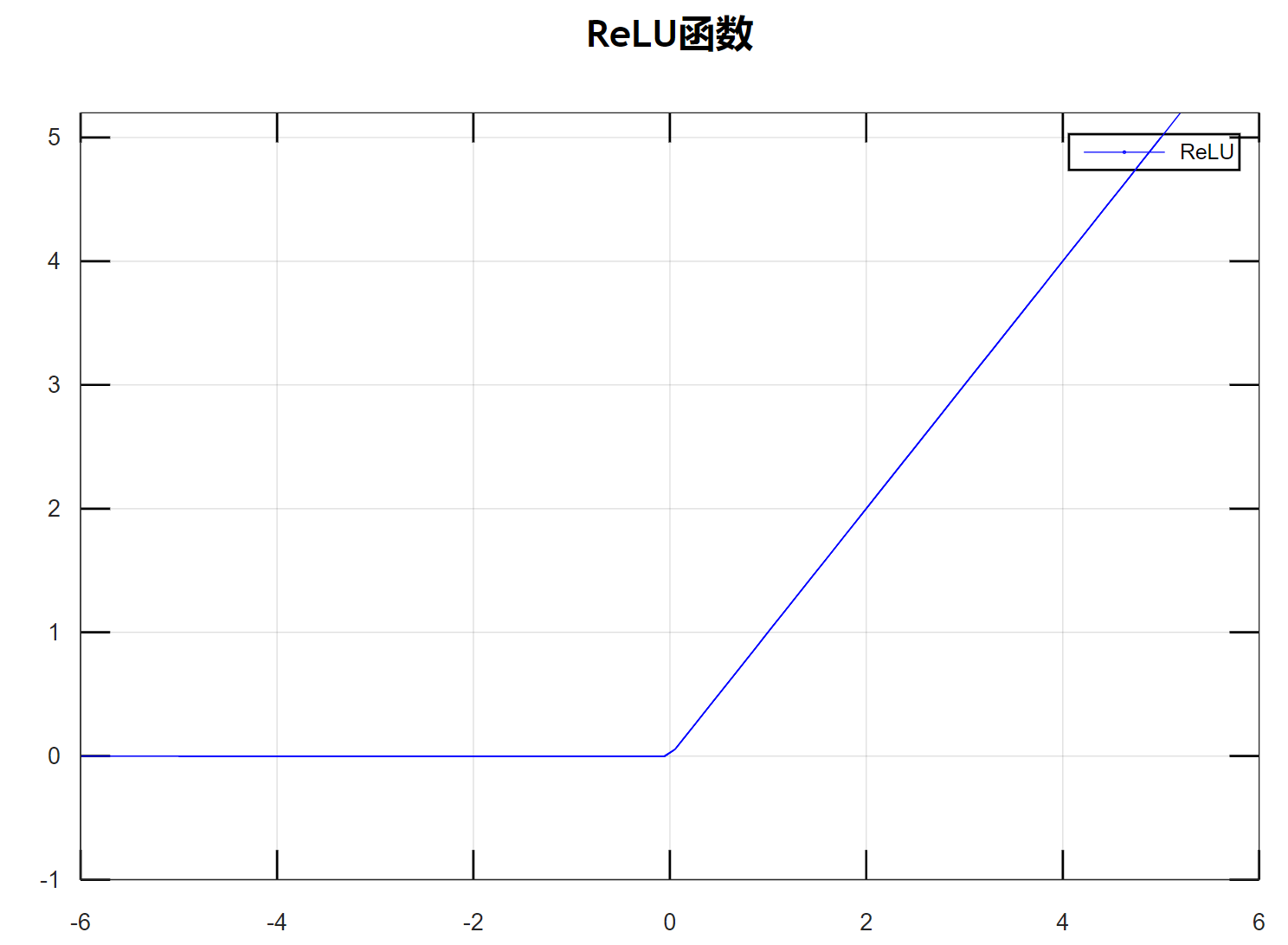
激活函数(Activation Function)是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。激活函数对于人工神经网络模型去学习、理解复杂的非线性函数,具有十分重要的作用。
如果不使用激活函数,每一层输出都是上一层输入的线性运算,无论神经网络有多少层,最终的输出只是输入的线性组合,相当于感知机。如果使用了激活函数,将非线性因素引入到网络中,使得神经网络可以任意逼近任何非线性函数,能够应用到更多的非线性模型。
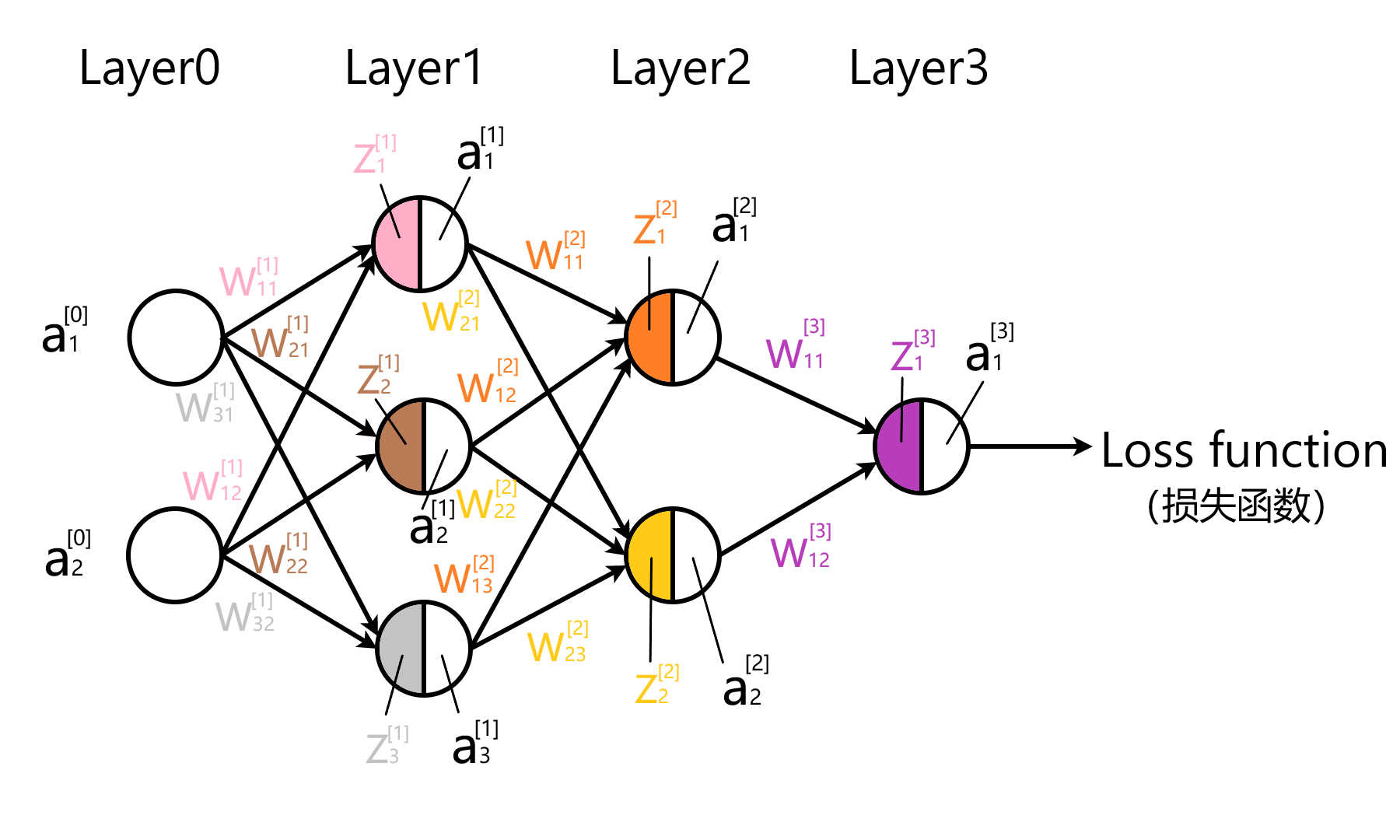
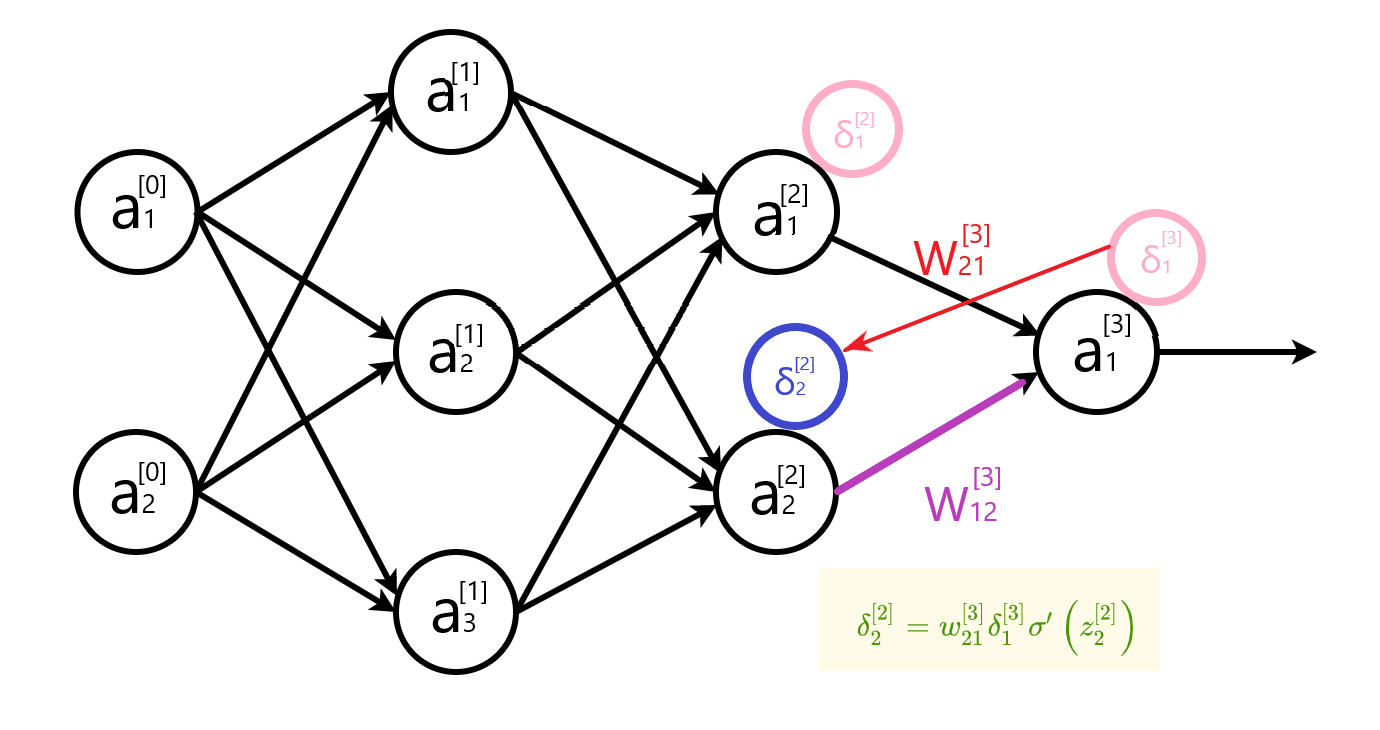
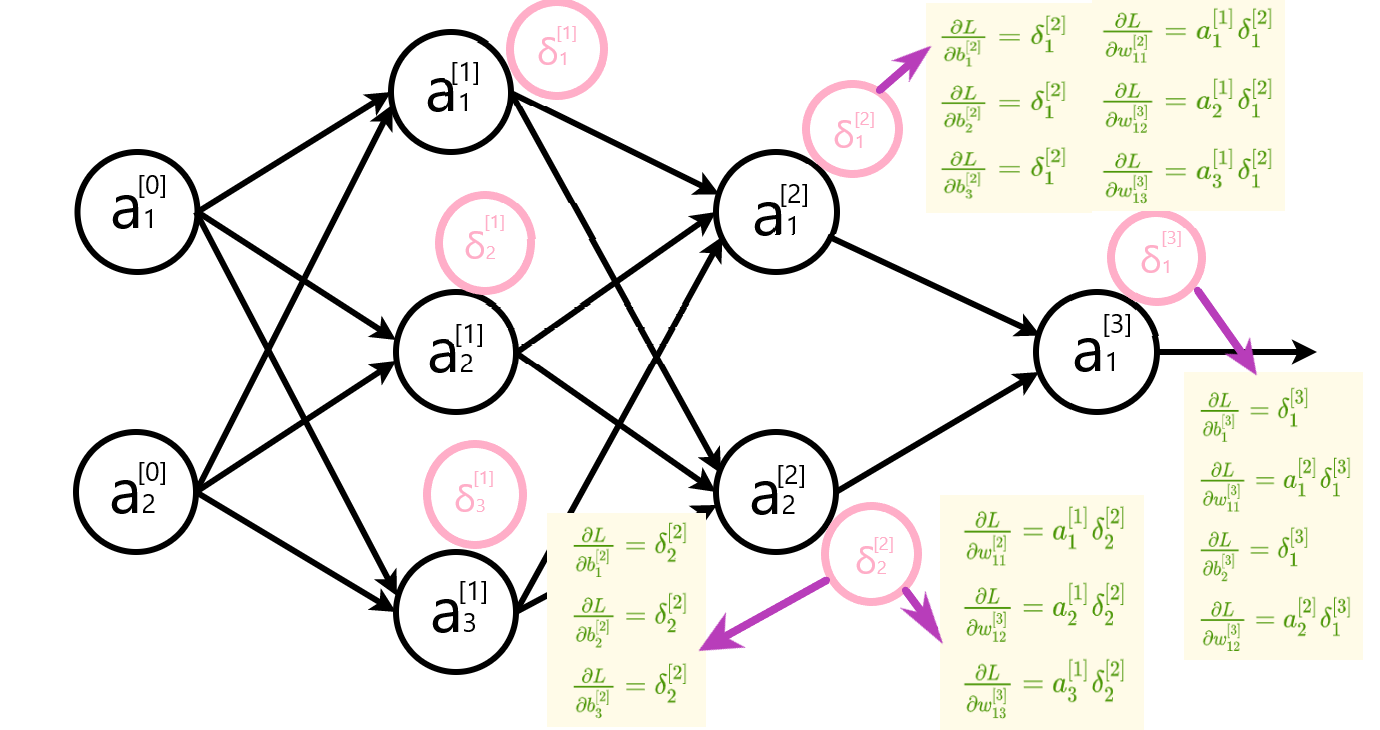
第0层是输入层(2个神经元),第1层是隐含层(3个神经元),第2层是隐含层(2个神经元),第3层是输出层。
$$
a_{j}^{[l]}=\sigma(z_{j}^{[l]})=\sigma\left(\sum_{k} w_{j k}^{[l]} a_{k}^{[l-1]}+b_{j}^{[l]}\right)
$$
$w^{[1]}=\left[\begin{array}{lll}w_{11}^{[1]} & w_{12}^{[1]} & \ w_{21}^{[1]} & w_{22}^{[1]} & \ w_{31}^{[1]} & w_{32}^{[1]}\end{array}\right]$ $w^{[2]}=\left[\begin{array}{lll}w_{11}^{[2]} & w_{12}^{[2]} & w_{13}^{[2]} \ w_{21}^{[2]} & w_{22}^{[2]} & w_{23}^{[2]}\end{array}\right]$
$b^{[1]}=\left[\begin{array}{l}b_{1}^{[1]} \ b_{2}^{[1]} \ b_{3}^{[1]}\end{array}\right]$ $b^{[2]}=\left[\begin{array}{l}b_{1}^{[2]} \ b_{2}^{[2]}\end{array}\right]$
进行线性矩阵运算。
$z^{[1]}=\left[\begin{array}{lll}w_{11}^{[1]} & w_{12}^{[1]} & \ w_{21}^{[1]} & w_{22}^{[1]} & \ w_{31}^{[1]} & w_{32}^{[1]}\end{array}\right] \cdot\left[\begin{array}{c}a_{1}^{[0]} \ a_{2}^{[0]}\end{array}\right]+\left[\begin{array}{l}b_{1}^{[1]} \ b_{2}^{[1]} \ b_{3}^{[1]}\end{array}\right]=\left[\begin{array}{c}w_{11}^{[1]} a_{1}^{[0]}+w_{12}^{[1]} a_{2}^{[0]}+b_{1}^{[1]} \ w_{21}^{[1]} a_{1}^{[0]}+w_{22}^{[1]}a_{2}^{[0]}+b_{2}^{[1]} \ w_{31}^{[1]}a_{1}^{[0]}+w_{32}^{[1]}a_{2}^{[0]}+b_{3}^{[1]}\end{array}\right]$
矩阵形状 (3,2) (2,1) (3,1) (3,1)
$z^{[2]}=\left[\begin{array}{ccc}w_{11}^{[2]} & w_{12}^{[2]} & w_{13}^{[2]} \ w_{21}^{[2]} & w_{22}^{[2]} & w_{23}^{[2]}\end{array}\right] \cdot\left[\begin{array}{c}a_{1}^{[1]} \ a_{2}^{[1]} \ a_{3}^{[1]}\end{array}\right]+\left[\begin{array}{c}b_{1}^{[2]} \ b_{2}^{[2]}\end{array}\right]=\left[\begin{array}{c}w_{11}^{[2]} a_{1}^{[1]}+w_{12}^{[2]} a_{2}^{[1]}+w_{13}^{[2]} a_{3}^{[1]}+b_{1}^{[2]} \ w_{21}^{[2]} a_{1}^{[1]}+w_{22}^{[2]} a_{2}^{[1]}+w_{23}^{[2]} a_{3}^{[1]}+b_{2}^{[2]}\end{array}\right]$
矩阵形状 (2,3) (3,1) (2,1) (2,1)
那么,前向传播过程可以表示为: $$ a^{[l]}=\sigma\left(w^{[l]} a^{[l-1]}+b^{[l]}\right) $$ 上述讲述的前向传播过程,输入层只有1个列向量,也就是只有一个输入样本。对于多个样本,输入不再是1个列向量,而是m个列向量,每1列表示一个输入样本。m个$a^{[l-1]}$列向量组成一个m列的矩阵$A^{[l-1]}$。
$A^{[l-1]}=\left[\begin{array}{cccc}| & | & \cdots & | \ a^{l-1} & a^{l-1} & \dots & a^{l-1} \ | & | & \dots & |\end{array}\right]$
多样本输入的前向传播过程可以表示为: $$ \begin{array}{c} Z^{[l]}=w^{[l]} \cdot A^{[l-1]}+b^{[l]} \ A^{[l]}=\sigma\left(Z^{[l]}\right) \end{array} $$ 与单样本输入相比,多样本$w^{[l]}$和$b^{[l]}$的定义是完全一样的,不同的只是$Z^{[l]}$和$A^{[l]}$从1列变成m列,每1列表示一个样本的计算结果。
在有监督的机器学习算法中,我们希望在学习过程中最小化每个训练样例的误差。通过梯度下降等优化策略完成的,而这个误差来自损失函数。
损失函数用于单个训练样本,而成本函数是多个训练样本的平均损失。优化策略旨在最小化成本函数。下面例举几个常用的损失函数。
- 绝对值损失函数(
$L_{1}$ 损失函数):
- 平方损失函数(
$L_{2}$ 损失函数):
- 交叉熵损失:
反向传播的基本**:通过计算输出层与期望值之间的误差来调整网络参数,使得误差变小(最小化损失函数或成本函数)。反向传播基于四个基础等式,非常简洁优美,但想要理解透彻还是挺烧脑的。
假设函数
$\nabla_{x} f(x)=\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_{1}} \ \frac{\partial f(x)}{\partial x_{2}} \ \vdots \ \frac{\partial f(x)}{\partial x_{n}}\end{array}\right]$
同理,假设函数
$\nabla_{A} f(A)=\left[\begin{array}{cccc}\frac{\partial f(A)}{\partial A_{11}} & \frac{\partial f(A)}{\partial A_{12}} & \dots & \frac{\partial f(A)}{\partial A_{13}} \ \frac{\partial f(A)}{\partial A_{21}} & \frac{\partial f(A)}{\partial A_{22}} & \dots & \frac{\partial f(A)}{\partial A_{2 n}} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial f(A)}{\partial A_{m 1}} & \frac{\partial f(A)}{\partial A_{m 2}} & \dots & \frac{\partial f(A)}{\partial A_{m n}}\end{array}\right]$
可以简化为:
$\left(\nabla_{A} f(A)\right){i j}=\frac{\partial f(A)}{\partial A{i j}}$
注意:梯度求解的前提是函数
矩阵相乘
矩阵 $A=\left[\begin{array}{cc}1 & 2 \ 3 & 4\end{array}\right]$,矩阵 $B=\left[\begin{array}{cc}-1 & -2 \ -3 & -4\end{array}\right]$
$A B=\left[\begin{array}{ll}1 \times-1+2 \times-3 & 1 \times-2+2 \times-4 \ 3 \times-1+4 \times-3 & 3 \times-2+4 \times-4\end{array}\right]=\left[\begin{array}{cc}-7 & -10 \ -15 & -22\end{array}\right]$
矩阵对应元素相乘
使用符号$\odot$表示:
$A \odot B=\left[\begin{array}{cc}1 \times-1 & 2 \times-2 \ 3 \times-3 & 4 \times-4\end{array}\right]=\left[\begin{array}{cc}-1 & -4 \ -9 & -16\end{array}\right]$
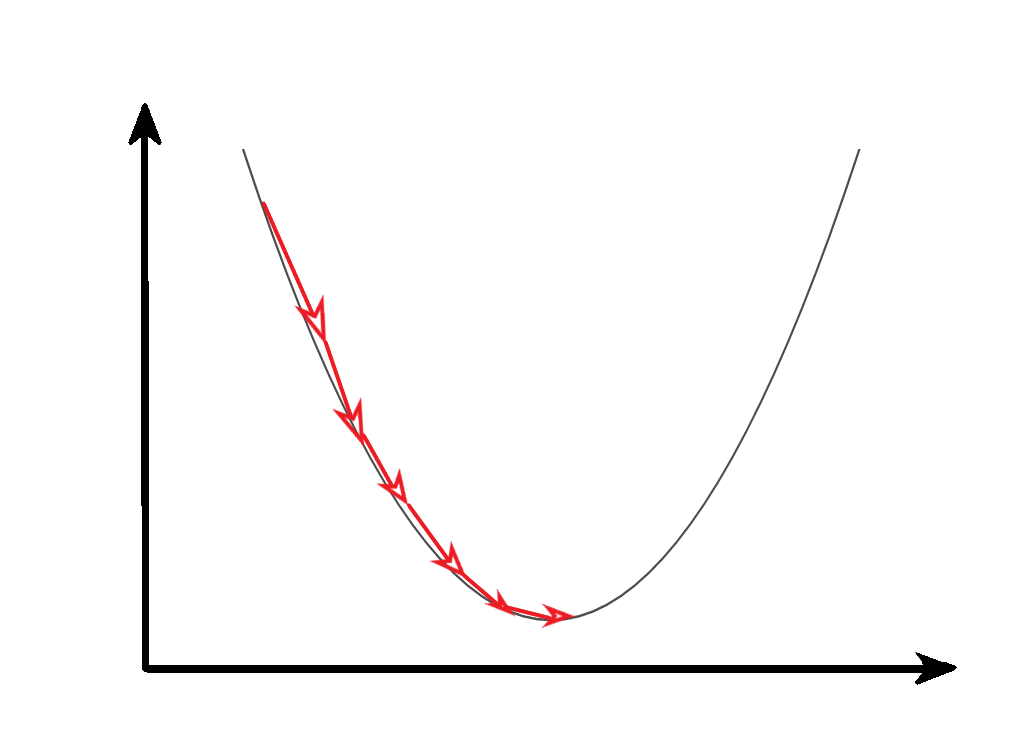
从几何意义,梯度矩阵代表了函数增加最快的方向,沿着梯度相反的方向可以更快找到最小值。
反向传播的过程就是利用梯度下降法原理,逐步找到成本函数的最小值,得到最终的模型参数。
要想最小化成本函数,需要求解神经网络中的权重
定义网络中第
其中
每一层的误差向量可以表示为:
$\delta^{[l]}=\left[\begin{array}{c}\delta_{1}^{[l]} \ \delta_{2}^{[l]} \ \vdots \ \delta_{n}^{[l]}\end{array}\right]$
L表示输出层层数。以下用
写成矩阵形式是:
$\delta^{[L]}= \left[\begin{array}{c}\frac{\partial L}{\partial a_{1}^{[L]}} \ \frac{\partial L}{\partial a_{2}^{[L]}} \ \vdots \ \frac{\partial L}{\partial a_{j}^{[L]}}\end{array}\right] \odot\left[\begin{array}{c}\sigma^{\prime}\left(z_{1}^{[L]}\right) \ \sigma^{\prime}\left(z_{2}^{[L]}\right) \ \vdots \ \sigma^{\prime}\left(z_{j}^{[L]}\right)\end{array}\right]$
表示成公式: $$ \delta^{[L]}=\nabla_{a} L \odot \sigma^{\prime}\left(z^{[L]}\right) $$
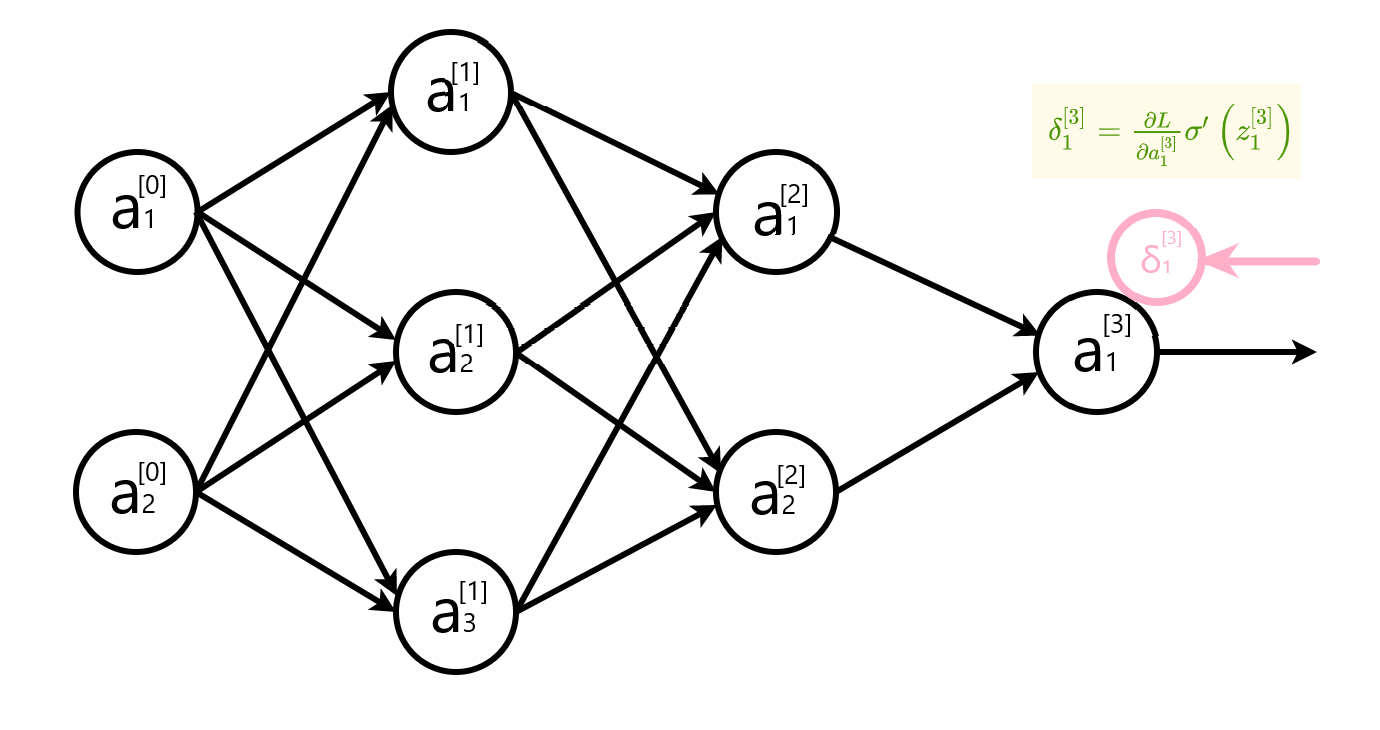
计算输出层的误差
输出层不一定只有一个神经元,可能有多个神经元。成本函数是每个输出神经元的损失函数之和,每个输出神经元的误差与其它神经元没有关系,所以只有$k=j$ 的时候值不是0。
当$k\neq j$ 时,$\frac{\partial L}{\partial z_{j}^{[L]}}=0$ ,简化误差
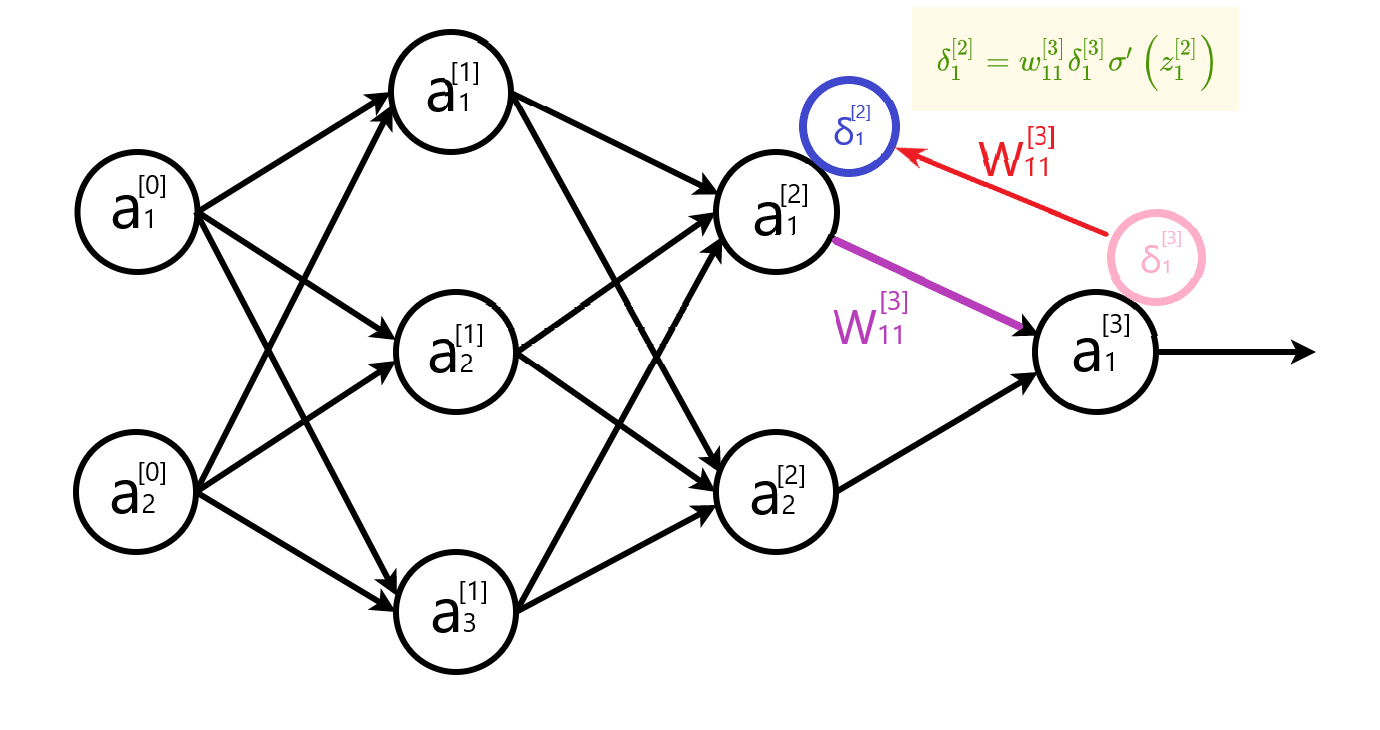
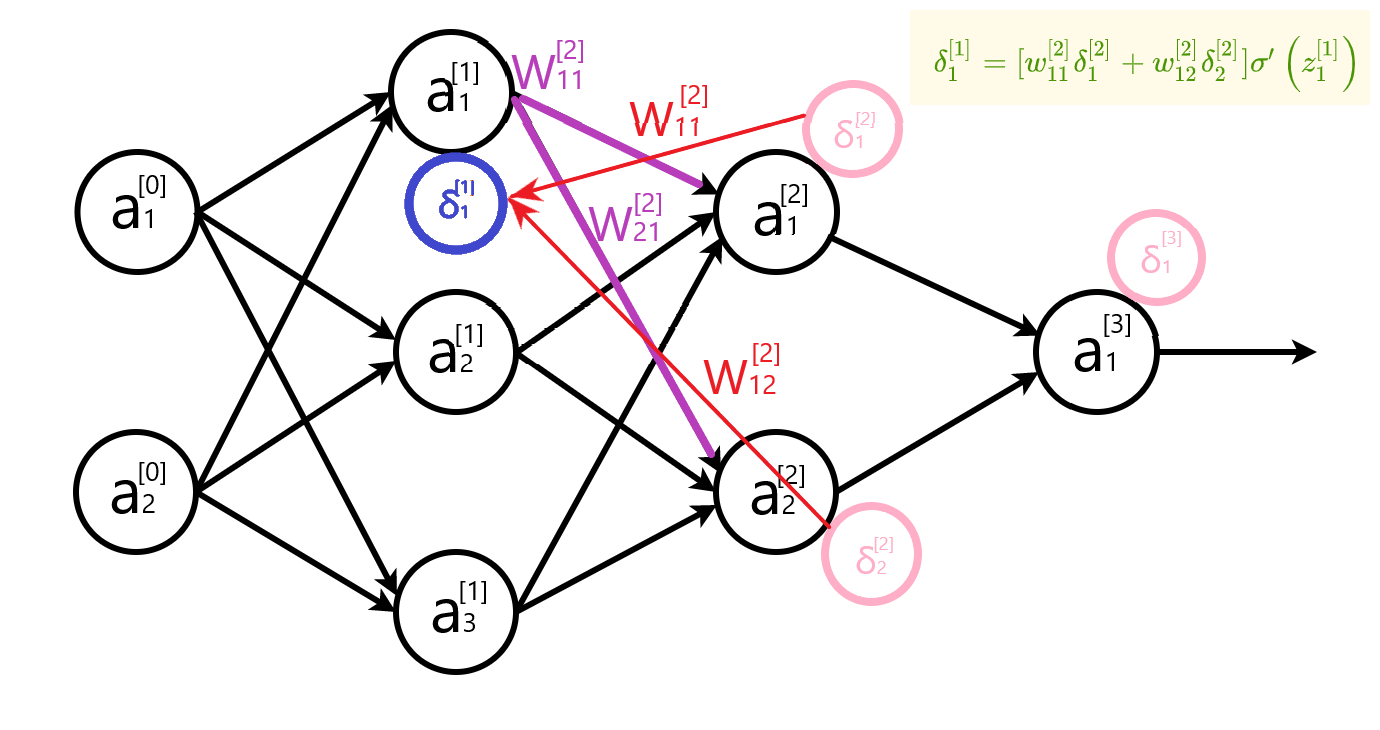
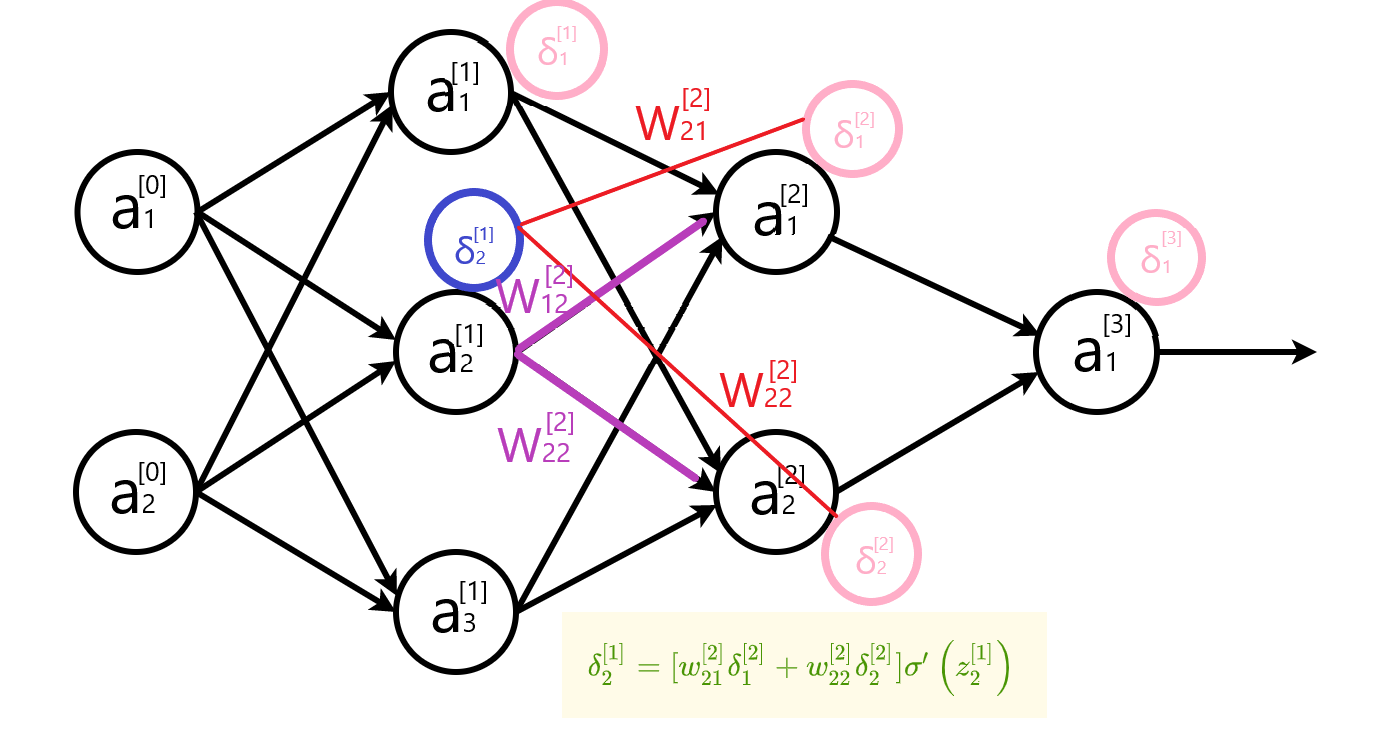
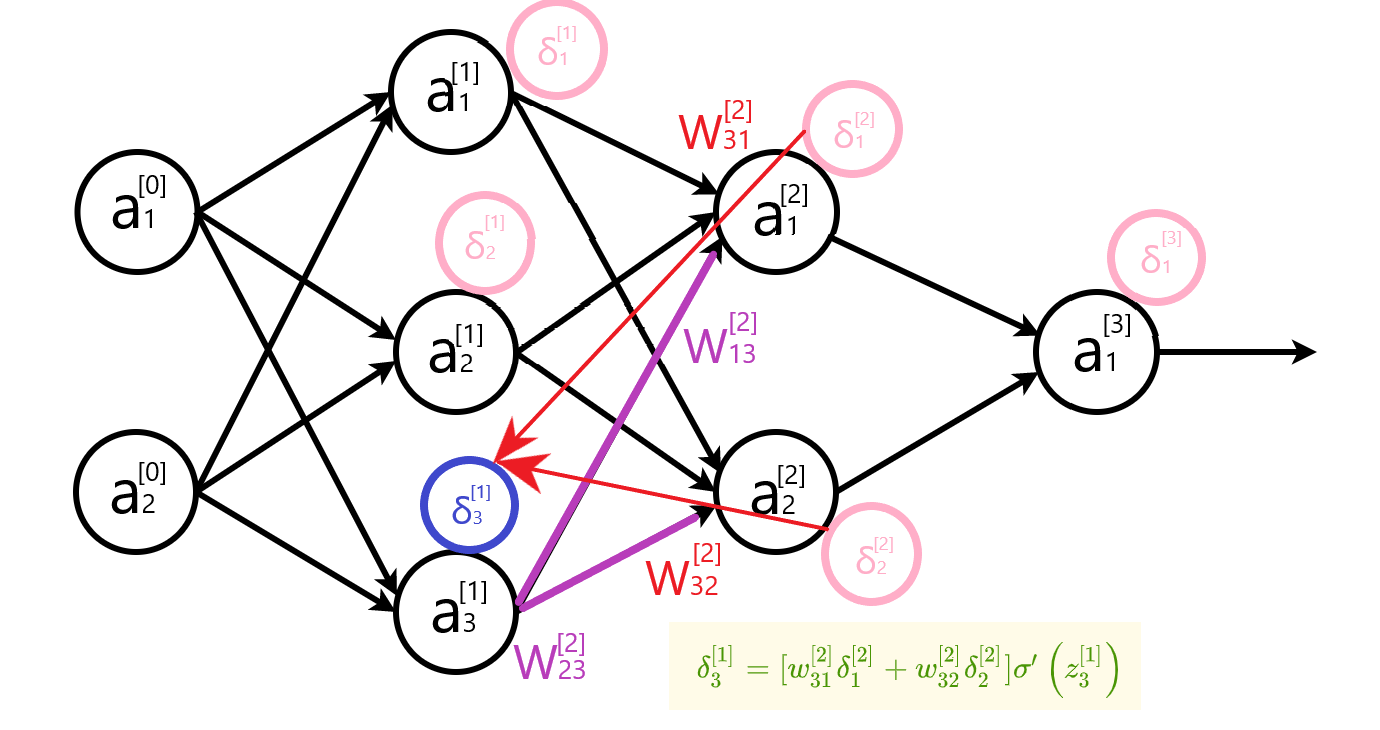
写成矩阵形式:
$\delta^{[l]}=\left[\begin{array}{lll} \left[\begin{array}{lll}w_{11}^{[l]} & w_{12}^{[l]} & \dots & w_{1k}^{[l]} \ w_{21}^{[l]} & w_{22}^{[l]} & \dots & w_{2k}^{[l]} \ \vdots & \vdots & \ddots & \vdots\ w_{j1}^{[l]} & w_{j2}^{[l]} & \dots & w_{jk}^{[l]} \end{array}\right] \left[\begin{array}{c}\delta_{1}^{[l+1]} \ \delta_{2}^{[l+1]} \ \vdots \ \delta_{k}^{[l+1]}\end{array}\right] \end{array}\right] \odot\left[\begin{array}{c}\sigma^{\prime}\left(z_{1}^{[l]}\right) \ \sigma^{\prime}\left(z_{2}^{[l]}\right) \ \vdots \\sigma^{\prime}\left(z_{j}^{[l]}\right)\end{array}\right]$
矩阵形状:(j,k) * (k,1)
权重矩阵的形状从(k,j)转置变成(j,k)。
表示成公式: $$ \delta^{[l]}=\left[w^{[l+1]^{T}} \delta^{[l+1]}\right] \odot \sigma^{\prime}\left(z^{[l]}\right) $$ 推导
对
根据链式法则
写成矩阵形式:
$\frac{\partial L}{\partial b^{[l]}}=\left[\begin{array}{c}\delta_{1}^{[l]} \ \delta_{2}^{[l]} \ \vdots \ \delta_{j}^{[l]}\end{array}\right]=\delta^{[l]}$
矩阵形状:(j,1)
$\frac{\partial L}{\partial w^{[l]}}=\left[\begin{array}{c}\delta_{1}^{[l]} \ \delta_{2}^{[l]} \ \vdots \ \delta_{j}^{[l]}\end{array}\right] \left[\begin{array}{c}a_{1}^{[l]} a_{2}^{[l]}\dots a_{k}^{[l]} \end{array}\right]$
矩阵形状:(j,1) * (1,k) = (j,k)
注意:$\frac{\partial L}{\partial w^{[l]}}$ 是一个dim
表示成公式: $$ \begin{array}{c} \frac{\partial L}{\partial b^{[l]}}=\delta^{[l]} \ \frac{\partial L}{\partial w^{[l]}}=\delta^{[l]} a^{[l-1] T} \end{array} $$ 推导
L 对
L 对
根据梯度下降法原理,朝着梯度的反方向更新参数
$$
\begin{array}{c}
b_{j}^{[l]} \leftarrow b_{j}^{[l]}-\alpha \frac{\partial L}{\partial b_{j}^{[l]}} \
w_{j k}^{[l]} \leftarrow w_{j k}^{[l]}-\alpha \frac{\partial L}{\partial w_{j k}^{[l]}}
\end{array}
$$
写成矩阵形式:
$$
\begin{array}{l}
b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial L}{\partial b^{[l]}} \
w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial L}{\partial w^{[l]}}
\end{array}
$$
这里的
计算输出层误差
计算隐藏层误差
隐藏层误差公式写成矩阵形式
计算参数变化率
最后更新每层的参数。
| 说明 | 公式 |
|---|---|
| 输出层误差 | |
| 隐含层误差 | |
| 参数变化率 | $\begin{array}{c}\frac{\partial L}{\partial b^{[l]}}=\delta^{[l]} \\frac{\partial L}{\partial w^{[l]}}=\delta^{[l]} a^{[l-1] T}\end{array}$ |
| 参数更新 | $$\begin{array}{l}b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial L}{\partial b^{[l]}} \w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial L}{\partial w^{[l]}}\end{array}$$ |
多样本输入使用的成本函数与单样本不同。假设单样本的成本函数是交叉熵损失函数。
那么,对于m个样本输入,成本函数是每个样本的成本总和的平均值。
单样本输入的每一层的误差是一个列向量
$\delta^{[l]}=\left[\begin{array}{c}\delta_{1}^{[l]} \ \delta_{2}^{[l]} \ \vdots \ \delta_{n}^{[l]}\end{array}\right]$
而多样本输入的每一层的误差不再是一个列向量,变成一个m列的矩阵,每一列对应一个样本的向量。那么多样本的误差定义为:
$dZ^{[l]}=\left[\begin{array}{c}\delta^{l} \delta^{l} \dots \delta^{l}\end{array}\right]=\left[\begin{array}{c}\delta_{1}^{l}&\delta_{1}^{l}&\dots&\delta_{1}^{l} \ \delta_{2}^{l}&\delta_{2}^{l}&\dots&\delta_{2}^{l} \ \vdots & \vdots & \ddots & \vdots \ \delta_{n}^{l}&\delta_{n}^{l}&\dots&\delta_{n}^{l} \end{array}\right]$
因为$dZ^{[l]}$的维度是
| 说明 | 公式 |
|---|---|
| 输出层误差 | |
| 隐含层误差 | |
| 参数变化率 | |
| 参数更新 | $\begin{array}{l}b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial C}{\partial b^{[l]}} \w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial C}{\partial w^{[l]}}\end{array}$ |