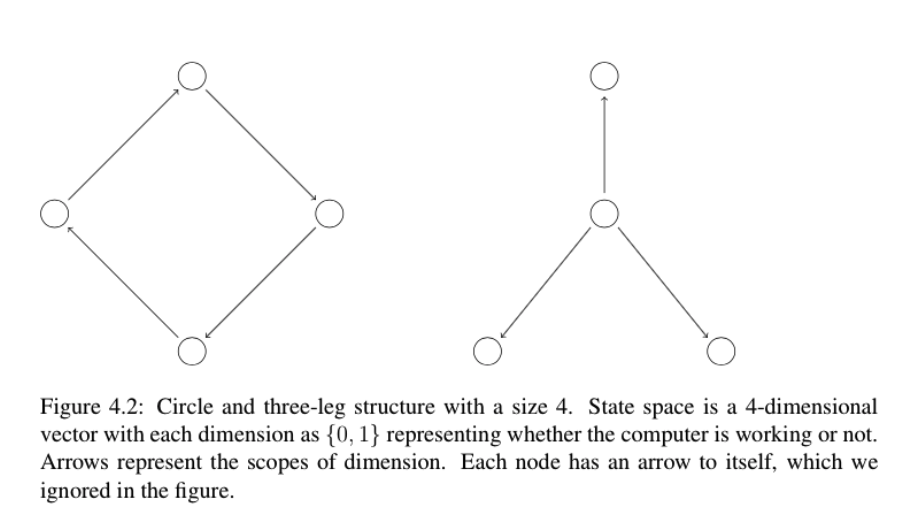
This repository is the code for the paper Reinforcement Learning in Factored MDPs: Oracle-Efficient Algorithms and Tighter Regret Bounds for the Non-Episodic Setting.
We implemented the approximate solution using the method in Efficient Solution Algorithms for Factored MDPs. The linear programing is solved by calling Pulp.
# required Python 3.7
pip install PuLP==2.1from fmdp import *
# generate a threeleg environment
# two parameters for the difficulties of each env
alpha1 = 0.1
alpha2 = 0.1
n_factor_s = 4
n_factor_a = 1; n_state = 2; n_action = n_factor_s + 1
mdp = generate_3leg(n_factor_s, n_factor_a, n_state, n_action, alpha1 = alpha1, alpha2 = alpha2)
# view transition and reward function
mdp.p
mdp.rWe compare three solutions here:
- Accurate solution using LP (Equ (7) in Guestrin 2003)
- Approximate solution using single basis function without variable elimination
- Approximate solution using single basis function with variable elimination (Figure 5 in Guestrin 2003)
Single basis function approximate value function using single basis funcitons: $$ f_i(x) = x_i\ f(x) = \sum_{i = 1}^m w_i f_i(x) $$
O = order(mdp) # generate orders for variables elimination
# Accurate solution
mdp.FactoredALP(O, basis = "accurate")
mdp.opt.lp_problem.solve()
lambda_star = mdp.opt.obj.value()
print(lambda_star)
# Approximate solution (fast)
mdp.FactoredALP(O)
mdp.opt.lp_problem.solve()
lambda_app1 = mdp.opt.obj.value()
print(lambda_app1)
# Approximate solution without variable elimination (slow)
mdp.FactoredDirect()
mdp.opt.lp_problem.solve()
lambda_app2 = mdp.opt.obj.value()
print(lambda_app2)
print(lambda_app1 == lambda_app2)Online learning experiments are implemented in simple_exp.py. Three algorithms are implemented:
- DORL (our method)
- PSRL
- Factored Rmax
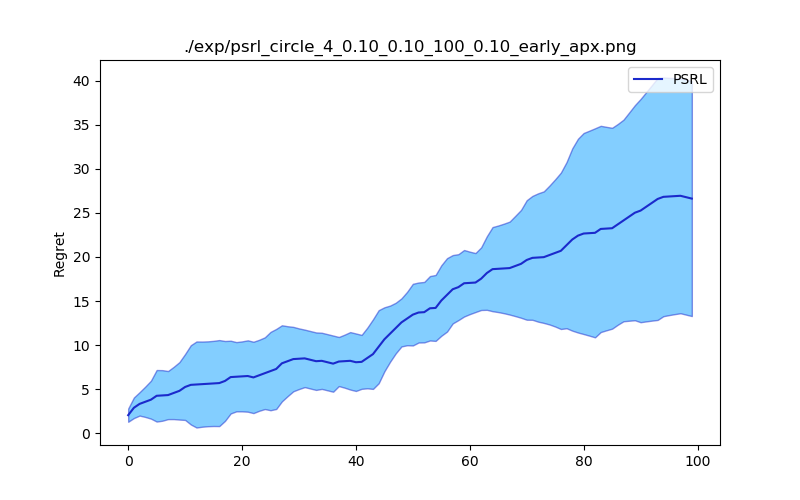
python simple_exp.py --alg psrl -t 100 -n 5Available hyper-parameters:
parser.add_argument("--alg", help="Algorithms to use: psrl, dorl, rmax", default = "psrl")
parser.add_argument("-p", help="Type of MDP to solve: circle or threeLeg", default = "circle")
# Two parameters for environment generating.
parser.add_argument("-a", help="alpha1", type = float, default = 0.1)
parser.add_argument("-b", help="alpha2", type = float, default = 0.1)
parser.add_argument("-s", help="Number of state factors", type = int, default = 4)
parser.add_argument("-n", help="Number of replicate", type = int, default = 20)
parser.add_argument("-t", help="Numer of steps for each replication", type=int, default = 100)
# Fixed horizon uses the stopping criterion in DORL paper. If it is set False, we use the criterion in Ouyang 2017.
parser.add_argument("-f", help="Whether to use fixed horizon", type = bool, default = False)
parser.add_argument("--acc", help="Whether to use accurate planner to calculate regrets. If it is set False, use approximate planner", type = bool, default = False)
parser.add_argument("--show", help="Show results every `show` steps", type = int, default = 100)
parser.add_argument("--seed", help="Random seed", type = int, default = 1)
parser.add_argument("-d", help="Directory to save results", default = "./exp/")
parser.add_argument("-c", help="Hyper-parameter c for DORL or PSRL", type = float, default = 0.1)
parser.add_argument("-m", help="m for Rmax", type = int, default = 100)Sample output.