AutoInv

Ben Mildenhall, Fall 2017

Summary

AutoInv can automatically invert (a subset of) functions written in native Python and Numpy.

Background

Consider the following program structure, which is a common occurence in code for manipulating arrays in image processing and scientific computing:

The T operators typically consist of array arithmetic and reshaping operations, and F is some sort of processing function. There are prime marks on the 1 and 0 in the last two boxes since T0->1 and T1->0 do not have to be perfect inverses - T1->0 could be the inverse of a differently parametrized version of T0->1.

Examples:

T0->1 takes an [H, W] image array to a [H/K, W/K, K^2] array by reshaping each K x K block of the image into a third channel. F decimates to a single [H/K, W/K] image, then uses a superresolution technique to recover all K^2 elements of the final channel. T1->0 reshapes from [H/K, W/K, K^2] back to [H, W].
T0->1 maps from pixel space for camera A to world space. F processes points in 3D (could be a no-op). T1->0 maps from world space to pixel space for camera B. Here, T0->1 and T1->0 are not perfect inverses, but T10 is still made up of a reversed list of the primitive functions used in T01, just with different parameters.

It is tedious and bug-prone to write out T1->0 automatically when it can be inferred from T0->1. The goal of this project is to provide a proof of concept for using an Autograd-like tracing system to do exactly this.

Approach

Recording the execution trace

AutoInv uses a simplified version of the Autograd model for recording the execution traces of functions.

Every use of the np.ndarray type is wrapped by a Box subclass, whose only additional members are node and _trace fields. The Node class is used to record the trace of a single wrapped Numpy function call, including fields

fun: the function being called,
args, kwargs: the args and kwargs provided,
value: the value returned by the function,
parent_argnums: argnums corresponding to the boxed arguments, and
parents: a list of pointers to the node fields of all such boxed args.

After executing a block of Python code that uses AutoInv's wrapped version of Numpy, the parents list for each boxed Numpy array will trace out the complete execution DAG.

This is a simplified version of the function wrapper we apply to the Numpy library:

def primitive(f_raw):

    def f_wrapped(*args, **kwargs):
        value = f_raw(*_args, **kwargs)

        # boxes is a list of pairs (argnum, boxed_arg)
        # with one entry for every boxed argument in args
        boxes, trace = find_top_boxed_args(args)
        parent_argnums = [a for a, _ in boxes]
        parents = [b.node for _, b in boxes]

        # box the output and record a Node 
        # if value is a numpy array
        if isinstance(value, _np.ndarray):
            # view() allows you to treat a numpy
            # array as any of its subclasses
            value = value.view(Box)
            value.node = Node(value, f_wrapped, args, kwargs, parent_argnums, parents)
            value._trace = trace
            
        return value
        
    return f_wrapped

The _trace field is used to keep track of which boxed arguments are "active" in the current trace: currently, AutoInv supports inversion for Python functions of a single Numpy array argument. Extraneous Numpy arrays that are used in computation but are not descendants of the function argument should not be traced for inversion. As in Autograd, this is implemented by seeding the function argument's _trace with an integer from a simple Python generator that returns n the n-th time it is called. So every time we start a new trace, we know that find_top_boxed_args should only look for the boxed args with the largest _trace value. Basic tracing code:

def trace(fun, x):
    with trace_stack.new_trace() as t:
        print 'New trace with value {}'.format(t)
        x.node = anp.Node(None, None, None, None, [], [])
    	x._trace = t
        end_box = fun(x)
        if isinstance(end_box, anp.Box) and end_box._trace == t:
            print 'Trace successful'
            return end_box
        else:
            warnings.warn("Output seems independent of input.")
            return end_box, None

Function inversion

After getting the function trace, we make a backwards pass over the stored DAG to create the inverse function (without necessarily calling it yet). We'd like to automatically replicate something like this:

We do this by hand-writing an inverse generator for each primitive function in the Numpy library we'd like to be able to invert. These generators are stored in a dictionary primitive_invs where the keys are function pointers. Thus the process to look up a function and generate its inverse when given a node works as follows:

Look up inv_gen_argnum = primitive_invs[node.fun]
Evaluate inv_gen = inv_gen_argnum(argnum) for argnum = node.parent_argnums[0].
Evaluate inv_fn = inv_gen(node.value, *node.args, **node.kwargs).
Return inv_fn, which will be passed y when the node inverse must be evaluated.

The outer wrapper with the argnum parameter allows us to use a different inverse generator depending on which function argument was boxed. Note: AutoInv currently only supports function inversion when a single argument is active in the trace, e.g., the inverse of x0 + x1 where x0 and x1 have the same _trace value cannot be calculated.

The inv_gen function in the third step takes the function output and all inputs and uses it to generate an inverse for that Numpy function given those values in the trace. For example, for roll, the inverse generator is

lambda ans, x, shift, axis=None  : lambda g: anp.roll(g, -shift, axis=axis))

The generator here uses the shift and axis values from args to instantiate an inverse that can reverse that particular call to roll. Once evaluated, the inner lambda can be stored in the node to be later run (perhaps many times) when the inverse function is actually called.

For a binary function like subtract, we need an inverse for both argnum=0 and argnum=1, so we use something like this:

def subtract_inv_gen_argnum(argnum):
    assert argnum < 2
    if argnum==0:
        return lambda ans, x, y : lambda g : g + y
    else:
        return lambda ans, x, y : lambda g : g + y

We can also invert more complicated functions, such as matmul, by taking advantage of Numpy's linear algebra capabilities:

lambda ans, A, B: lambda g : np.linalg.solve(A, g)

After generating the inverse function for each node in our execution trace, we can run the whole inverse by passing an input array through the each node inverse in backwards order. (See function backward_pass in core.py.)

Note: in order to create an inverse, we need an actual Numpy array with the correct shape to pass through the function, since the size of the input array can affect the inverses of individual node objects along the trace. Autograd does not need this since the gradient of a function takes inputs in the same "space" as the original function, whereas our inverse functions take inputs with the shape of the function's output.

Example applications

Visit the Jupyter notebook file AutoinvExamples.ipynb to see working code for all of these examples.

HDR+ merge: inverting array reshaping

The HDR+ algorithm jointly denoises a burst of B images. In order to provide robustness, it merges the images together one small tile at a time. These tiles overlap by 50% in each dimension, so every pixel is actually contained in 4 different merged tiles. A smooth windowing function is used to interpolate between the 4 tiles.

A simple first use case for AutoInv is inverting the code that patches up an image into NxN pixel tiles with a potential N//2 pixel offset in each dimension:

def hdrplus_tiled(noisy, c, sig, N):
    sh = noisy.shape[0:2]
    buffer = np.zeros_like(noisy[...,0])
    
    for i in range(2):
        for j in range(2):
    
            def patchify(noisy):
                # Apply offset
                patches = anp.roll(noisy, shift=anp.array([-N//2*i, -N//2*j]), axis=(0,1))
                # Reshape to isolate NxN tiles
                sh_ = [sh[0]//N, N, sh[1]//N, N] + list(patches.shape[2:])
                patches = anp.reshape(patches, sh_)
                patches = anp.swapaxes(patches, 2, 1)
                return patches
                
            depatchify = core.make_inverse(patchify, noisy[...,0])
            
            patches = patchify(noisy)
            merged_patches = hdrplus_merge(patches, c, sig)      
            merged = depatchify(merged_patches) 
            
            buffer += merged
            
    return buffer

Here hdrplus_merge applies the interpolation window and removes the final axis of length B corresponding to the image stack in the course of merging each stack of NxN pixel tiles.

Something interesting here -- the patchify function is written so that it operates on the first two dimensions of the input while leaving the rest alone. This allows us to apply it as the forward operator for the full image stack noisy and the inverse operator for merged_patches, which lacks the final axis of size B. This is specified to AutoInv by passing noisy[...,0], which has our final desired output size, as an example input for make_inverse.

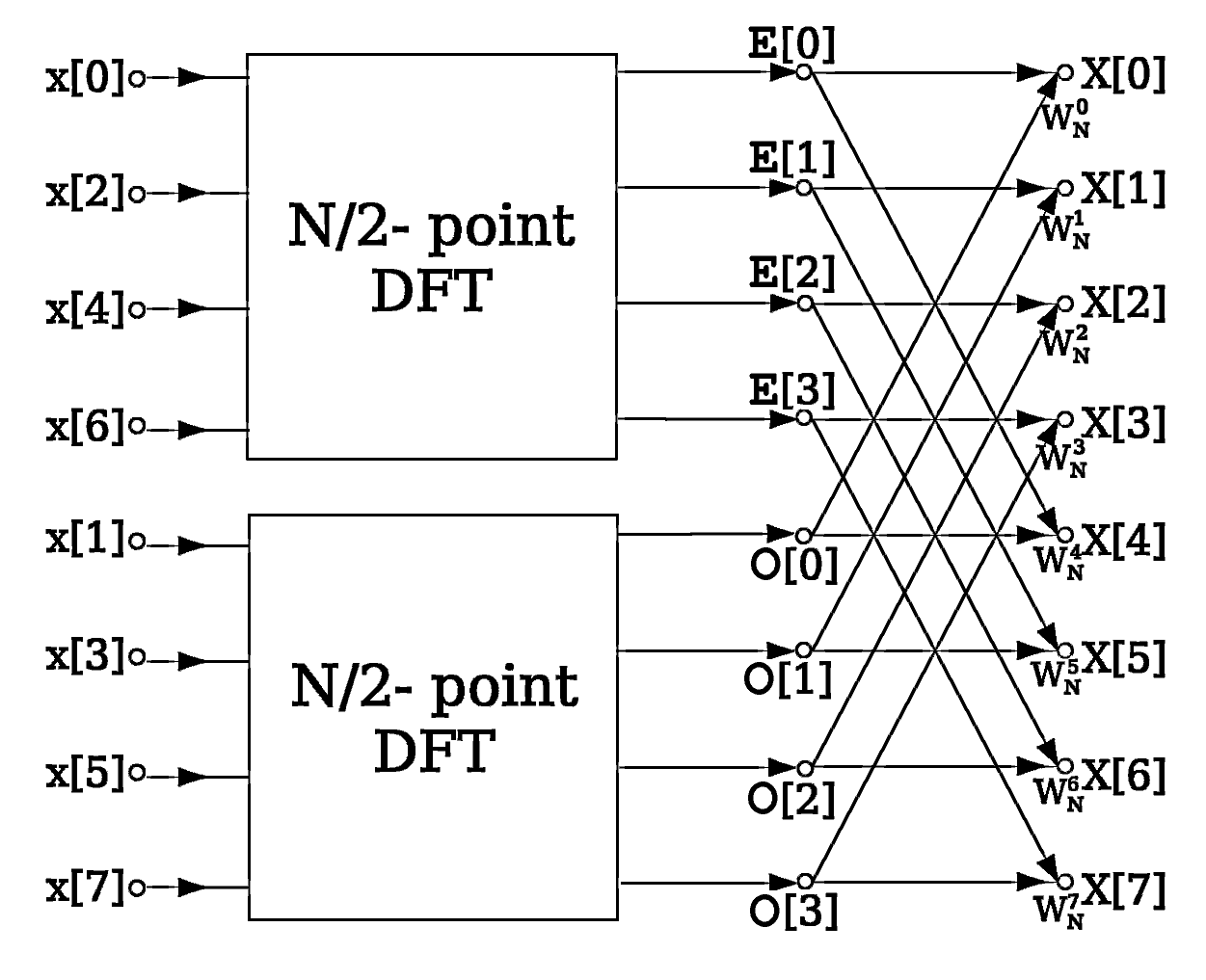
FFT: inverting through `matmul`

Here's a completely invertible implementation of the FFT "butterfly" algorithm that recurses on the even and odd halves of the input array as follows:

img credit

def twiddle(x):
    # Define the twiddle factors matrix
    N = x.shape[-1] + 0.
    omega = anp.exp(-2.j * anp.pi / (2*N) * anp.arange(0, N))
    a0 = anp.stack([anp.ones_like(omega),  omega], axis=-1)
    a1 = anp.stack([anp.ones_like(omega), -omega], axis=-1)
    a = anp.stack([a0, a1], axis=-2)

    # Merge 'even' and 'odd' halves with twiddle matrix
    x = anp.swapaxes(x, -1, -2)
    x = anp.expand_dims(x, -1)
    x = anp.matmul(a, x)
    x = anp.swapaxes(x, -2, -3)
    x = anp.reshape(x, list(x.shape[:-3]) + [-1])
    return x

# Cooley-Tukey 1D FFT over the last axis of x
def my_fft(x):
    if x.shape[-1] >= 2:
        # Separate 'even' and 'odd' halves of last axis
        x = anp.reshape(x, list(x.shape[:-1]) + [x.shape[-1]//2, 2])
        x = anp.swapaxes(x, -1, -2)
        # Recursively apply FFT to each half
        x = my_fft(x)
        # Use twiddle to merge the halves
        x = twiddle(x)
    return x

# 2D FFT on final two axes as two applications of 1D FFT
def my_fft2(x):
    x1 = my_fft(x)
    x2 = my_fft(anp.swapaxes(x1, -1, -2))
    x2 = anp.swapaxes(x2, -1, -2)
    return x2

M = 64
my_fft2_inv = core.make_inverse(my_fft2, anp.zeros([M,M]))
# my_fft2_inv is now an inverse for the 64x64 2D FFT

All the Numpy functions used above are invertible. In particular, matmul is invertible because each 2x2 twiddle factor matrix is nonsingular.

When tracing through the my_fft function, the recursive calls (and in fact, all function calls) are completely unrolled/inlined: as with Autograd, no control flow logic makes it into the trace. So the automatically generated inverse only works when applied to correctly sized inputs.

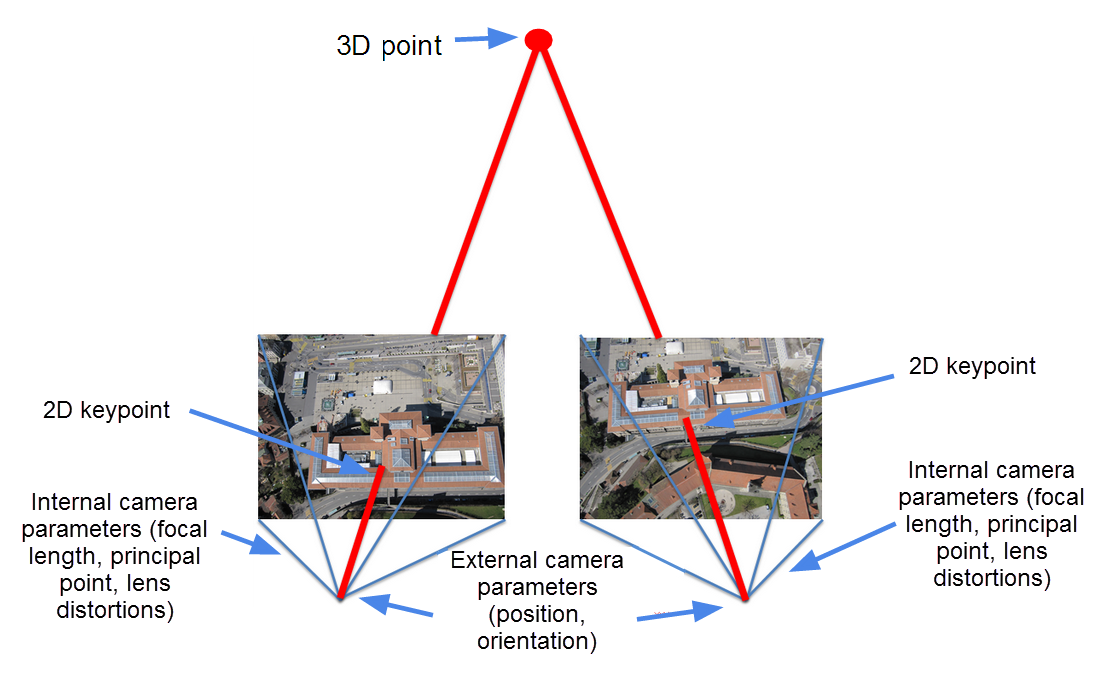
Camera projection: inverting with user-defined primitives

We can use AutoInv to invert a pixel space to world space reprojection function.