this is a simple simulation to gather various data from the system described and investigate how various variables and scheduling polcies impact system's behavior.
As we can see above Customers arrive with interarrival times that are exponentially distributed with a mean of 5(default) and we have an infinite queue that distributes the customer to one of the 5(default) servers chosen using round robbin or using a priority queue according to the policy. Each service follows a uniform distribution as shown in the figure. There a probability P that a customer who is not satisfied rejoins the queue and waits for him to serve again where variable I determines how many times the customer Is dissatisfied.
- python 3
- numpy
- simpy
- matplotlib
simply by coloning the repo and runing main.py using the below command.
"python3 main.py --iteration <> --numServers <> --arrivalTime <> --policy
- numServers is the number of servers working in parallel in our system.
- arrivalTime is the exponential interarrival mean of customers.
- iterations is the number of iteration the simulation will run and the reported the results is on the mean of all iterations to achieve more accurate results.
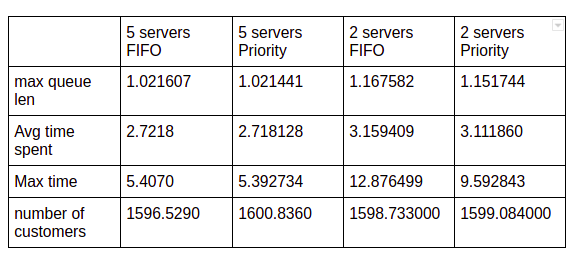
- if the number of servers increased suffciently then the policy won't make a difference since each customer that arrive to an empty queue.
- giving more priority to "dissatisfied" customers affects average time spent in system and effectively minimize it. Since serving "dissatisfied" customers will take less time. which is reflected when using Priority queue.
- we can mathematically prove, that the average service time should be arround 2.66 since in our setting we have 80% satisfied customer. \ we can assume if the num of servers is sufficent (no waiting in the queue) that time spent = 0.8*numCustomers*serviceTime(i=1) + 0.2*0.8*numCustomers*(serviceTime(i=1) + serviceTime(i=2)) + 0.2*0.2*numCustomers*(serviceTime(i=1) + serviceTime(i=2)+serviceTime(i=3)), we can neglect the remaining terms.