abel1231/vqe-qa

PyQPanda implementation of a variational quantum algorithm for finding the ground state energy of the molecule $H_6$

This is the official implementation of the VQE using the PyQPanda package for finding the ground state energy of the molecule $H_6$, whose geometry is given as:

geom = "H 1.300000 2.250000 0.000000, \
        H 3.900000 2.250000 0.000000, \
        H 5.200000 0.000000 0.000000, \
        H 3.900000 -2.250000 0.000000, \
        H 1.300000 -2.250000 0.000000, \
        H 0.000000 0.000000 0.000000"

whose FCI energy is -2.806471946359929.

Requirements

The code is based on python 3.8 and one can install all the required packages by

pip install -r requirements.txt

How to use

We use Jordan–Wigner transformation to get the Paili Hamiltonian of $H_6$ and save this Hamiltonian as numpy format in my_Hamiltonian.npz, so that it can be loaded directly without having to calculate it from scratch.

To run the code, one should run the script

python vqnet.py --layers 20

where the value of --layers must be 20, 48 or 65, indicating the number of parameters of the quantum circuit, and also indicating the layer counts of sub-circuits (i,e., singles or doubles ansatz) that need to be stacked to build the entire quantum circuit. A more detailed description is as follows.

We obtain the structural layout of the quantum circuit for solving the ground state energy of $H_6$, with the help of Adapt-VQE protocol which can be found in this site. We should mention that currently three available quantum circuits are provided, each of which has different number of parameters along with different structural layout. These information are saved in:

1. layer_20.txt
2. layer_48.txt
3. layer_65.txt

in which the first column serves as a counter, the second column represents the parameter of the corresponding ansatz to be estimated, and the remaining columns represent the qubits that the ansatz will control.

Results

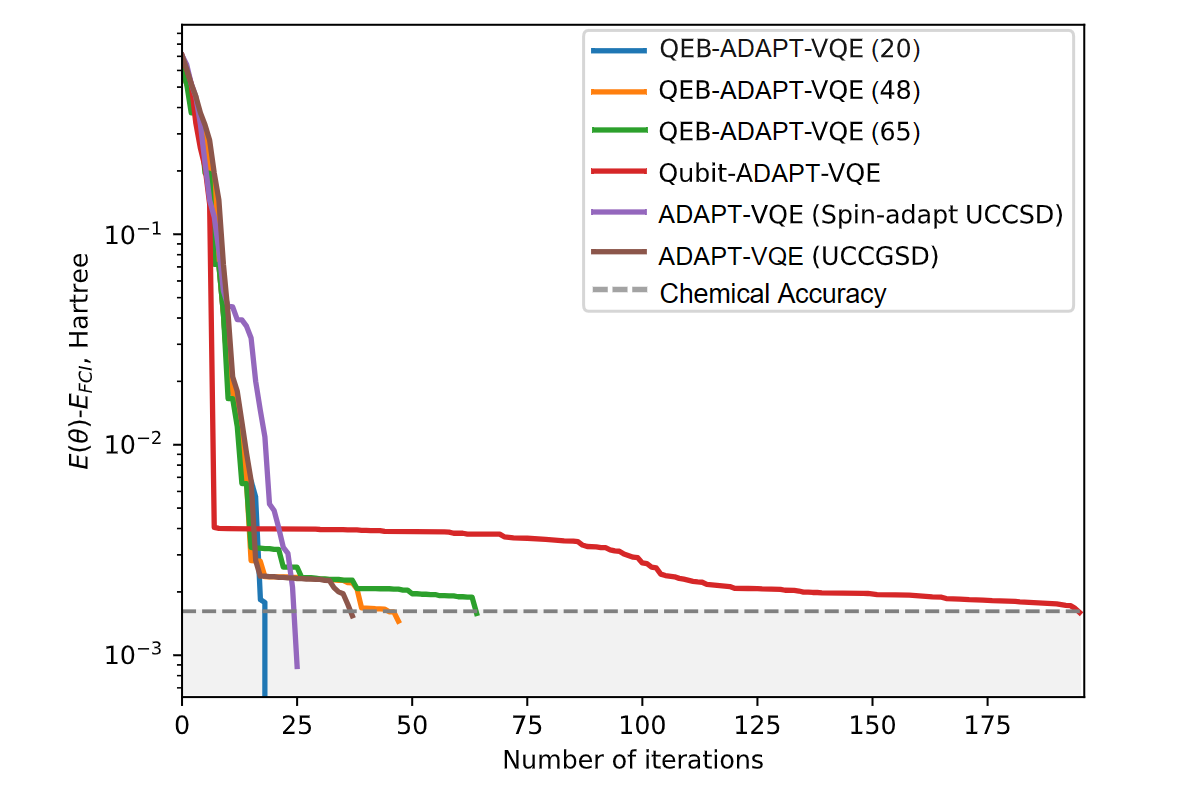
We report the ground state energy results and the running time (16 cores CPU) which are optimized by these three different quantum circuits:

	20-layer	48-layer	65-layer
Ground State Energy	-2.80650214	-2.80511892	-2.80540698
Time(s)	186s	531s	2880s

It can be seen that employing fewer layers results in reduced training time while maintaining chemical accuracy. Due to the resonable preprocess that sparcifies of the Hamiltonian matrix for faster convergence, the ground state energy of the 20-layer quantum circuit is noticeably lower than the FCI energy.

We also draw the curves of different quantum circuits for calculating ground state energy as the number of iterations increases