/visual_momentum

Visualizing gradient descent with momentum

Primary LanguageJupyter NotebookMIT LicenseMIT

Visualizing momentum

"Momentum" in optimization theory is usually introduced as an ad-hoc improvement over vanilla gradient descent. By leveraging moving averages over gradients, the optimizer manages not to get stuck in inflections or bad minimas. But momentum is so much more. Quoted from this brilliant article:

"For now — momentum is an algorithm for the book."

Reference: ME697 Advanced Scientific Machine Learning

Summary

Forget all about optimization and gradient descent for now and focus on basic mechanics.
If a object lies in a potential energy field, it experiences a force. The force acting at any point $x$ is proportional to $\nabla_x f(x)$ if the potential energy is given by $f(x)$.

Consider two worlds:

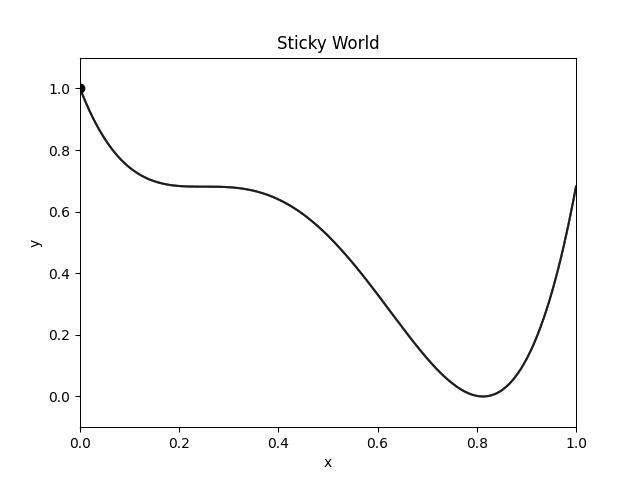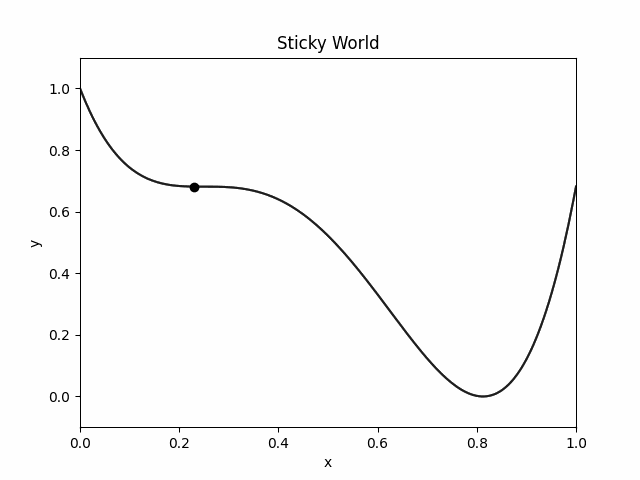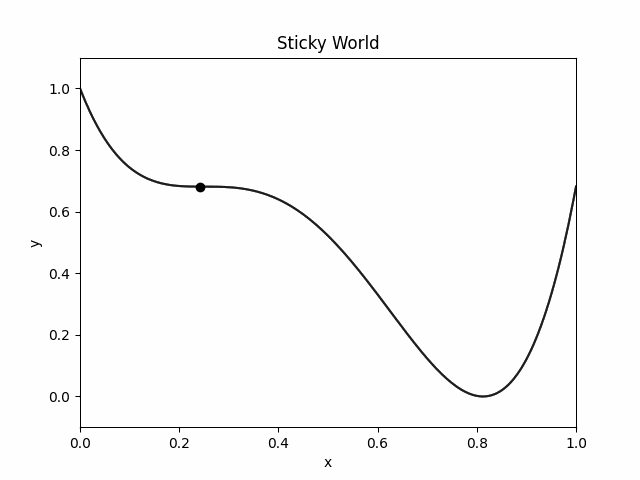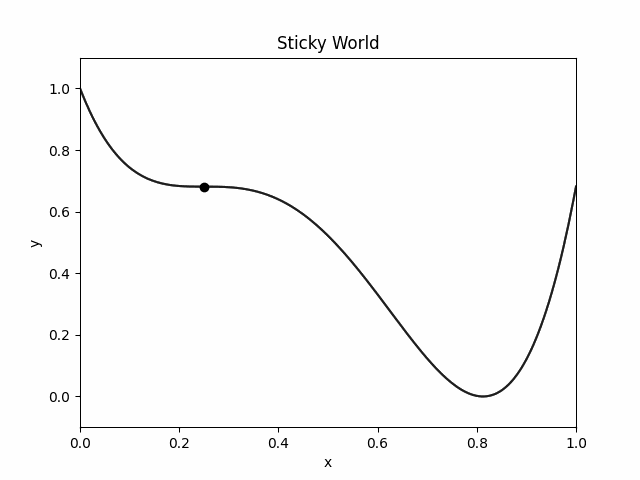
  1. Sticky World: The velocity of the object is proportional to the net force.
  2. Newton's World: The acceleration of the object is proportional to the net force.

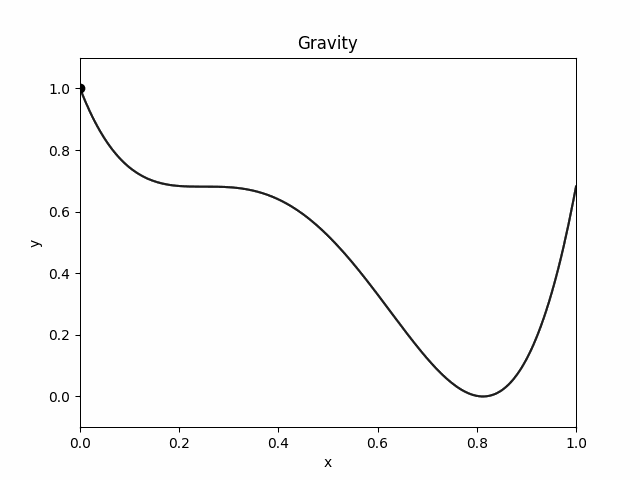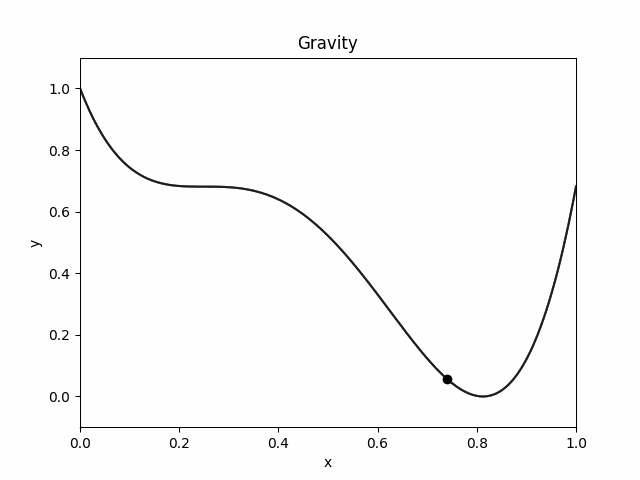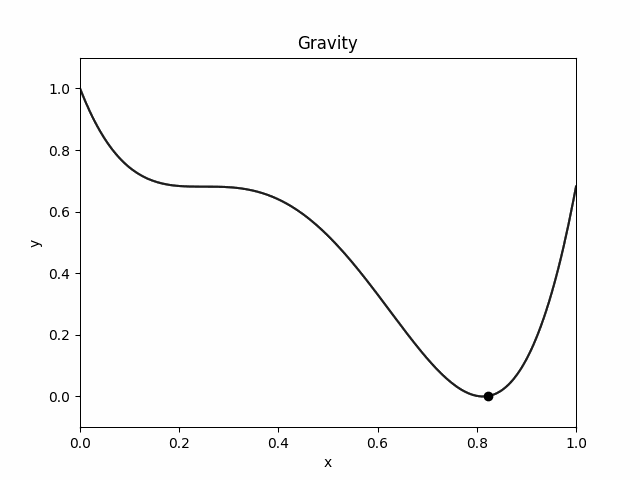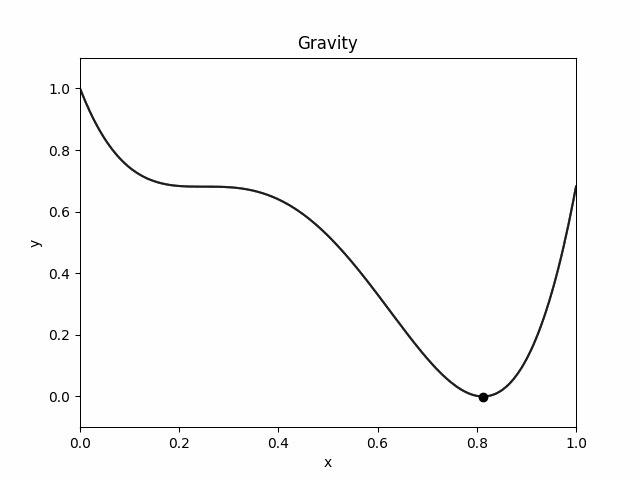
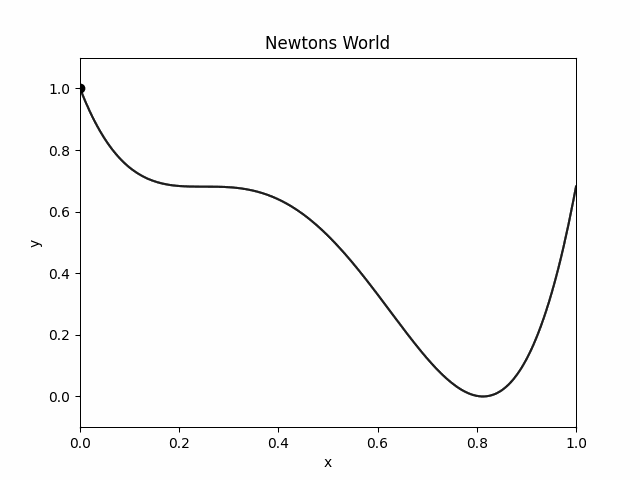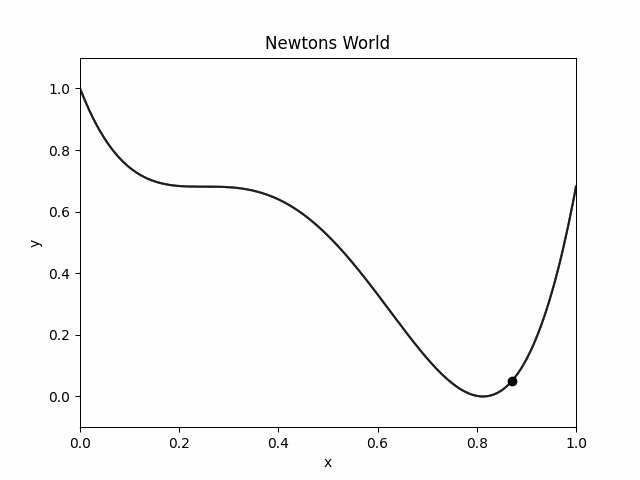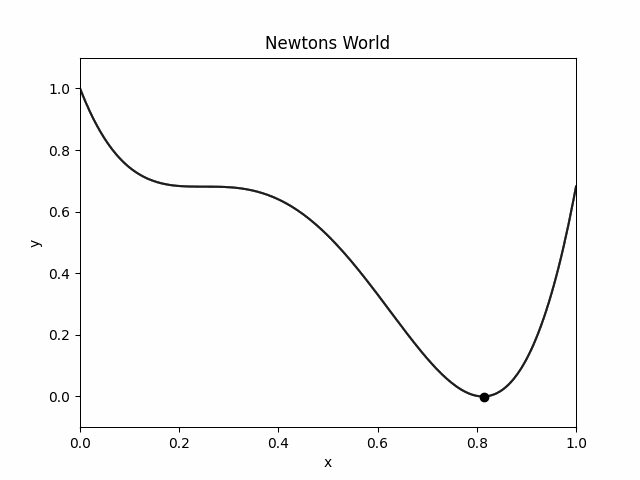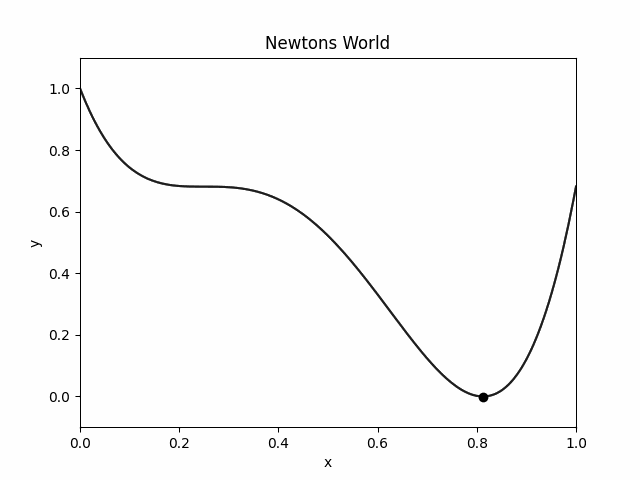
We imagine these world's in 1D and visualize them in 2D. On the X axis you have the position of the object. On Y axis you have the potential energy.

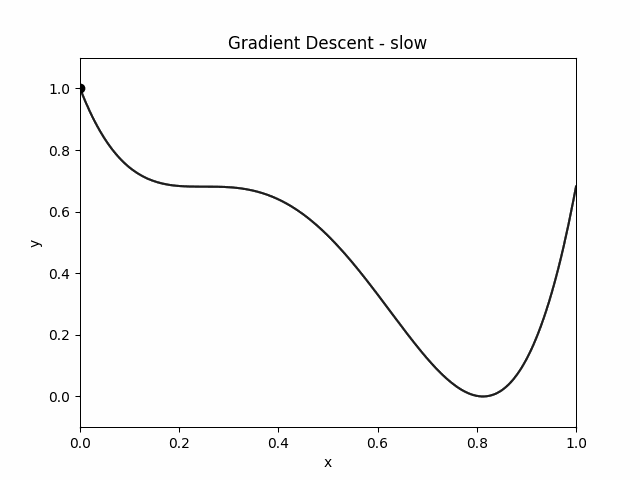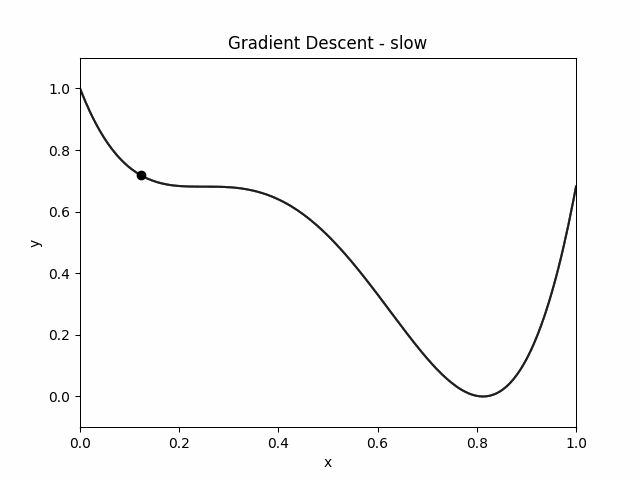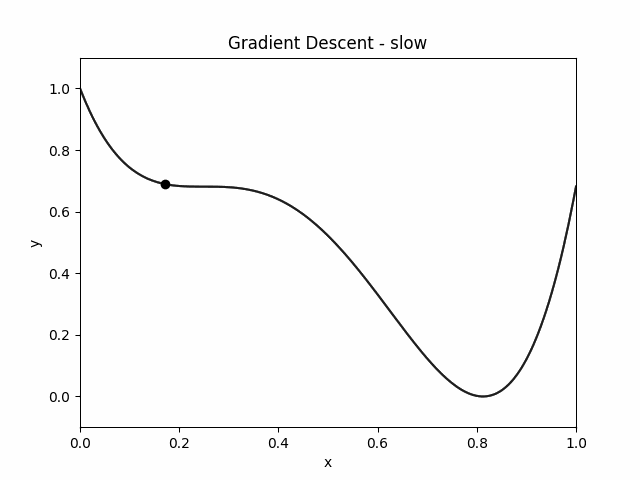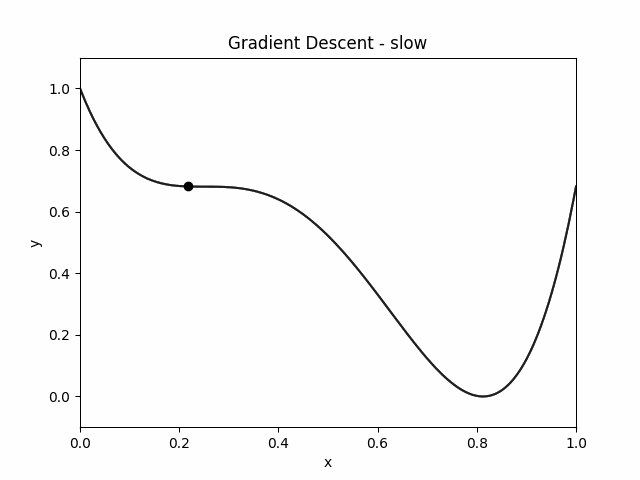
Here is how the object moves in `Sticky World':

alt text

Here is how the object moves in `Newton's World':

alt text Note: We have also employed a drag force here, acting in direction opposing the momentum, proportional to it.

Observations:

  1. There is no inertia in the sticky world. Any maxima, minima or inflection ($\nabla_x f(x) = 0$) makes the velocity/momentum of the object zero. The object stops.
  2. In newton's world, there is inertia. When force is zero, the object stops accelerating but it still moves.
  3. Newton's world has better chances of a object not getting stuck in shallows and inflections.

Conclusions:

  1. The sticky world is a direct analogy to gradient descent: $$m\dot{x} \propto -\nabla_x f$$ $$\dot{x} \propto -\nabla_x f$$ $$\lim_{{\delta t} \to 0} \frac{x_{t+\delta t} - x_t}{\delta t} \propto -\nabla_x f$$

Considering a discrete equivalent case: $$\frac{x_{n+1} - x_n}{\eta} = -\nabla_x f$$ $$x_{n+1} = x_n - \eta\nabla_x f$$

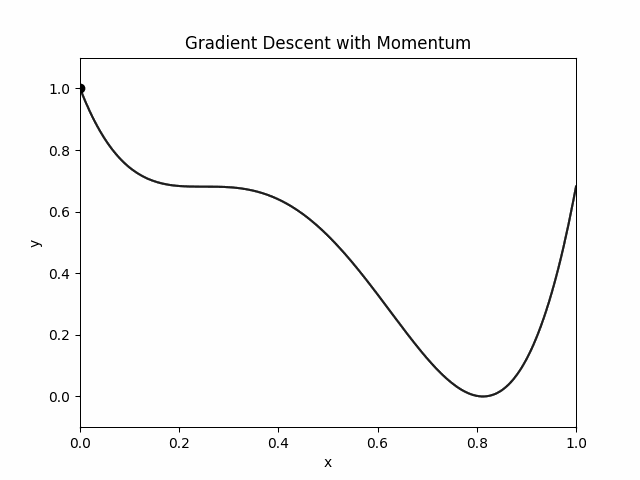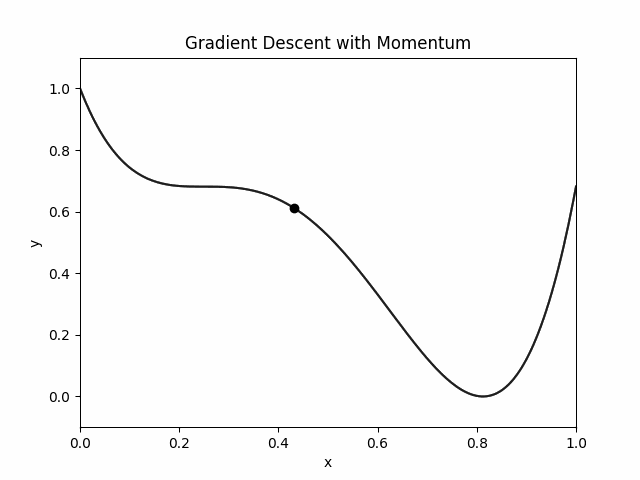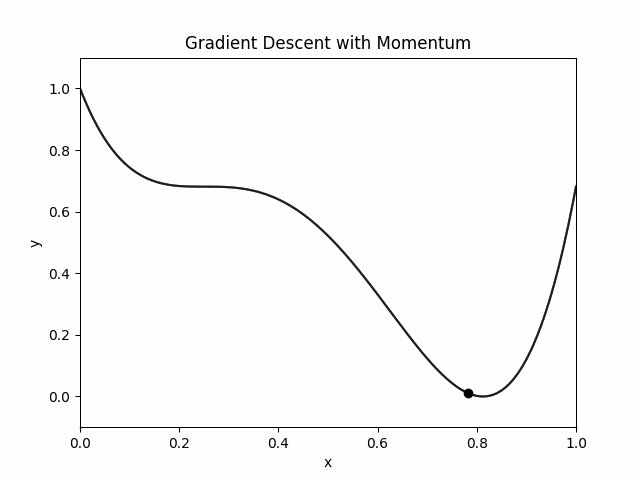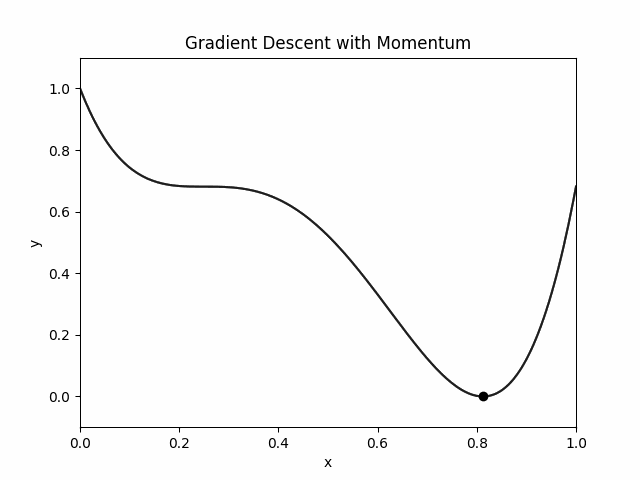
Let's just implement gradient descent on the potential energy function.

alt text

Doesn't this look identical to sticky world? It is important to note that these are two completely different solvers. The sticky world simulation was made by solving a ODE of a bead on a wire. This is just a iterative optimization animation.




2. Newton's world is an analogy to gradient descent with momentum: $$m\ddot{x} \propto \nabla_x f - \nu \dot{x}$$

This can be converted into a ODE, by chosing another variable $v = \dot{x}$, then solved, and then discretized as above, to show:

$$x_{n+1} = x_n + v_{n+1}$$ where, $$v_{n+1} = \beta v_n - \alpha \nabla f(x_n)$$

This is gradient descent with momentum!

alt text

Doesn't this look identical to newtons world? Again, note that these are two completely different solvers.

Visualizing optimization as a mechanics problem led to a better algorithm.



Incomplete

Full explanation

Newtonion Mechanics

For now, consider a body of mass $m$ at location $\textbf{x}$ with a force $\textbf{f}$ acting on it. Then Newton said we can say, $$m\ddot{\textbf{x}} = \textbf{f}$$ Now $f$ could be a single force, or it could be a vector addition of all the multiple forces acting on the body. It could also be a function of $\textbf{x}$, like in a spring.

Consider two forces, $\textbf{g}_x$ which is a function of space $\textbf{x}$ and another 'drag force' proportional to velocity $\dot{x}$ acting in the direction opposite to the movement.

$$m\ddot{\textbf{x}} = \textbf{g}_x - \nu \dot{\textbf{x}}$$

This is a pretty general mechanics problem statement - A free moving body operating under a force induced by a potential energy field and some friction. Consier, a 1-D space where each point $x$ ($x$ is a scalar now) has a potential energy given by a function, say $f(x)$. This induces on the particle a force proportional to $-\nabla_x f$ (or $\frac{df}{dx}$ or $f^{\prime}$, since we are dealing with scalars).

$$m\ddot{\textbf{x}} = -\eta \nabla_x f - \nu \dot{\textbf{x}}$$

Now for the hard part. You may have often tried to visualize a higher dimensional space in a lower dimension. I am going to ask you to do the opposite. Imagine this 1-D space in 2-D. The first dimension $x$ corresponds to the original $x$, the location of the point. The second dimension $y$ measures the potential energy of the body. Notice that this is still a 1D problem, since $y$ is completely known from $x$ using $y = f(x)$. The degree of freedom is still 1.

You can think of the body as a bead on a wire. The shape of the wire is $f(x)$. At any point the body experiences a force in the direction opposite to the slope of the wire, proportional to that slope. Simultaneously it also experiences a drag force opposite to the slope that is proportional to the speed of the bead $|\dot{x}\hat{i} + \dot{y}\hat{i}|$

(YET to complete)

alt text