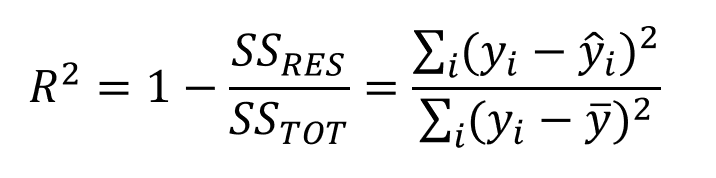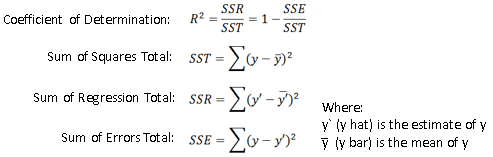Coefficient of Determination - Lab

Introduction

In the previous lesson we looked at the coefficient of determination, what it means and how it is calculated. In this lesson, we shall use the R-squared formula to calculate it in python and numpy.

Objectives

You will be able to:

Mathematically calculate R squared using a toy dataset
Calculate the coefficient of determination (R-squared) for a given regression line
Interpret the value of R-squared

Let's get started

Once a regression model is created, we need to decide how "accurate" the regression line is to some degree.

Here is the the equation for R-squared again:

potential new image

The equation is essentially 1 minus the division of the squared error of the regression (predicted) line, by the squared error of the mean y line .

The mean y line is quite literally the mean of all of the y values from the dataset. Thus, we do the squared error of the average y, and of the regression line.

The objective here is to learn how much of the error is actually just simply a result in variation in the data features, as opposed to being a result of the regression line being a poor fit.

Programming R-squared

Let's calculate R-squared in Python. The first step would be to calculate the squared error. Remember squared error is the sum of quares of difference between a given line and the ground truth (actual data points).

Create a function sq_err() that takes in y points for two lines as arrays, calculates the difference corresponding elements of these arrays, squares, and sums all the differences. The function should return the SSE value as we saw earlier.

# Calculate sum of squared errors between regression and mean line 
import numpy as np

def sq_err(ys_a, ys_b):
    """
    input
    y_a : regression line
    y_b : mean line
    
    return
    squared error between regression and true line (ss_tot)
    """
    pass

# Check the output with some toy data
Y_a = np.array([1,3,5,7])
Y_b = np.array([1,4,5,8])

sq_err(Y_a, Y_b)

# 2

Squared error, as calculated above is only a part of the coefficient of determination, Let's now build a function that would use sq_err() function above to calculate the value of r-squared by first calculating SSE and SST (SSres and SStot above) and then plugging these values into the R-squared formula. Perform following tasks

Calculate the mean of ys_real
Calculate SSE using sq_err()
Calculate SST using sq_err()
Calculate R-squared from above values using given formula.

# Calculate Y_mean , squared error for regression and mean line , and calculate r-squared

def r_squared(ys_real, ys_predicted):
    """
    input
    ys_real: real values
    ys_predicted: regression values
    
    return
    r_squared value
    """
    pass

# Check the output with some toy data
Y_real = np.array([1,3,5,7])
Y_pred = np.array([1,5,5,10])

r_squared(Y_real, Y_pred)

# 0.35

A very low value , but it was not from some real data. So now we have quite a few functions for calculating slope, intercept, bestfit line, plotting and calculating R-squared. In the next lab we'll put these all together to run a complete regression experiment.

Summary

In this lesson we saw how to calculate the R-squared value in python and numpy. Following lab will require you put all the functions from last few labs together to create a complete DIY regression experiment.