In this lesson, you'll get an introduction to some basic terminology regarding graphs and graph theory. To start, here's a graph!
You will be able to:
- Understand and explain fundamental concepts and terminology used in graph theory
- Describe a graph with its constituent components including nodes and edges
- Understand different types of networks with respect to their formations
To start, graphs are composed of two primary objects: nodes and edges. In the picture above, the nodes are the circles, while the lines that connect them are edges. Typically, nodes represent some entity such as a person, businesses, places, or webpages. In turn, edges then represent the relationships between these entities. For example, you might have a graph of a social network in which each node represents a person, and each edge represents whether those two individuals are connected or friends within the network.
As you can see, Jen is a well connected character in this scenario: she literally has a connecting edge with every other node in the graph! On the other hand, Jake is the least connected. He has no other connections other then Jen.
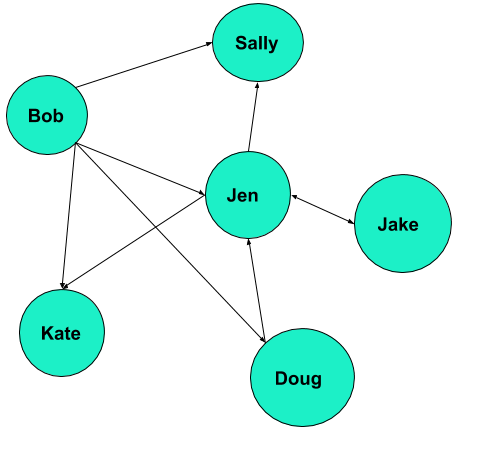
Another important concept in graph theory is the difference between directed and undirected graphs. The previous two examples have demonstrated undirected graphs. As the name implies, the edges in an undirected graph represent a mutual connection between two nodes. For example, the previous undirected graph could represent a mutual relationship such as "Friends" on Facebook or "Connections" on LinkedIn. In contrast, a direct graph looks like this:
As you can see, each of the edges now has an arrow indicating a direction. This scenario could represent an alternative type of social network such as Twitter in which individual's relationships are not necessarily mutual. Instead, Twitter users can follow other users to stay up to date with their activity. In the graph depicted above, Sally isn't following anyone. However, Both Bob and Jen are following Sally. There is also one mutual relationship depicted: Jake is following Jen and she is also following him.
Connectedness aims to quantify the number of edges attached to a node. In the diagrams above, Jen is undoubtedly the most connected of the individuals depicted. In the undirected graph, she was connected to everyone. Similarly, if your goal is to become an influencer, you're going to need to develop quite the following and become a very connected node. You'll explore more details in how connectedness is quantified in the upcoming lessons. For now, take some time to think about other implications of connectedness. For example, how might you be able to use connectedness to determine friend circles or cliques in social networks?
Path searching algorithms aim to find the shortest distance between any two nodes. This can then be used as a distance metric between nodes. Additionally, this can have interesting implications. For example, in a graph network of a website, a path searching algorithm might outline how many steps are required for a customer to move from the homepage, to browsing for an item, all the way through completing their purchase at checkout. You've actually already seen some basic examples of path searching algorithms in your work with traversing JSON files. There, you took a look at developing breadth-first versus depth-first recursive procedures to create an outline of the structure of an arbitrary JSON file.
In this lesson, you got a brief introduction to graph theory, including some basic definitions and foundational concepts. Remember that graphs are composed of primary objects called nodes and the relationships between those objects, known as edges. Additionally, graphs can be directed or undirected depending on the nature of the edges and the relationships between nodes.