Ankit Pensia, Shashank Rajput, Alliot Nagle, Harit Vishwakarma, Dimitris Papailiopoulos
This repository is the official implementation of Optimal Lottery Tickets via SubsetSum: Logarithmic Over-Parameterization is Sufficient .
Python 3.6.9, CUDA Version 10.2
Create a new python environment and install all package dependencies provided in requirements.txt. Once your environment is created, you can install the package dependencies by following the instructions below.
Only Experiment 1 from our paper uses a package called gurobipy, which is a package developed by Gurobi for modeling and solving optimization problems. gurobipy is installed differently depending on the package manager you're using:
- Install gurobipy with Anaconda
- Install gurobipy with pip
Once gurobipy is installed, a license is required to use the package; Gurobi offers unlimited free academic licenses. Information about downloading Gurobi and obtaining a license may be found at:
Gurobi also provides quickstart guides:
If you're using Anaconda, you just need to make sure that you add the Gurobi channel before installing from requirements.txt:
conda config --add channels http://conda.anaconda.org/gurobi
If you're using pip, see the above documentation to correctly setup gurobipy before installing it to your environment
Once you have completed the steps above, you may install all of the requirements to your environment with either of the following commands, depending on your package manager of choice.
pip install -r requirements.txt
or with
conda install --file requirements.txt
In both experiment directories, subset-sum and pruning, one or more bash scripts contain all commands to reproduce the results in the experiments provided in the paper. Please run
python main.py --helpin the terminal to see information about all arguments and their default values. In order to execute a script, run the following commands:
chmod u+x script.sh
only once to allow the script to be executable, and then run
./script.shto execute the script. If you would like to execute a script in the background and save all output to an output file, you may replace the above command with:
nohup ./script.sh > script.out &
Due to the hardness of the SubsetSum problem, it can take a long time to solve SubsetSum for all 397,000 parameters of a two-layer fully connected network. Our experiments use Gurobi's MIP solver. Our implemention will utilize all cores on a machine to solve each SubsetSum problem; to limit the core usage, we recommend running the experiment in the following way:
taskset -c 1-16 nohup ./run.sh > run.out &
This limits the number of cores used when executing run.sh to be between 1 and 16. Since every python script is run one at a time within run.sh, executing run.sh in this way will dedicate 1 to 16 cores to main.py. Nearly all of these cores will be dedicated to solving each SubsetSum instance once that part of the code is reached. The approximation of a two-layer fully connected network presented in our paper completed in about 21.5 hours on 36 cores of a c5.18xlarge AWS EC2 instance.
While most arguments to main.py are self-explanatory, there are a few arguments that would benefit from further explanation. Arguments --c and --epsilon determine the number of a_i coefficents used to approximate every weight in a target network via SubsetSum. The number of a_i coefficients is given by n = round(c * log2(1 / epsilon)). The --check_w_lt_eps argument, when enabled, will check whether a weight magnitude is less than or equal to epsilon before running SubsetSum on that weight value. If the magnitude is less than or equal to epsilon, the weight is approximated to be zero. This allows the script to terminate much earlier, have all weights approximations be within epsilon error, and the approximated target network will still have an accuracy very close to the target network.
In the subuset-sum directory, a run.sh script contains the necessary commands to reproduce our results.
Although most arguments used when running main.py are self-explanatory, some arguments and naming conventions deserve a more thorough explanation:
-
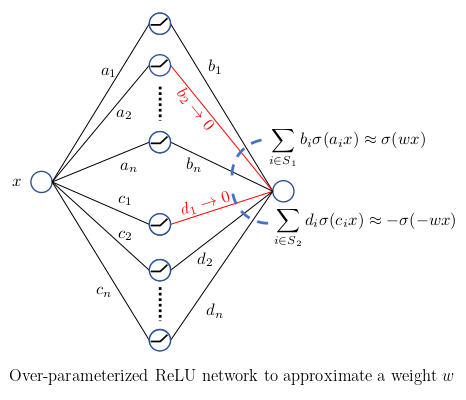
Throughout the code, the word "redundant" (sometimes shortened to the prefix "red") occurs frequently. This is a naming convention that refers to our structure. Essentially, our structure introduces some "redundancy" into a given architecture by replacing a single weight value with r different weight values, which are then pruned. The number of redundant units in a network with our structure is specified by the argument --redundancy. For example, running
python main.py --model "RedTwoLayerFC" --redundancy 5
instructs main.py to run an experiment for a two-layer fully connected network with our structure and 5 units of redundancy.
-
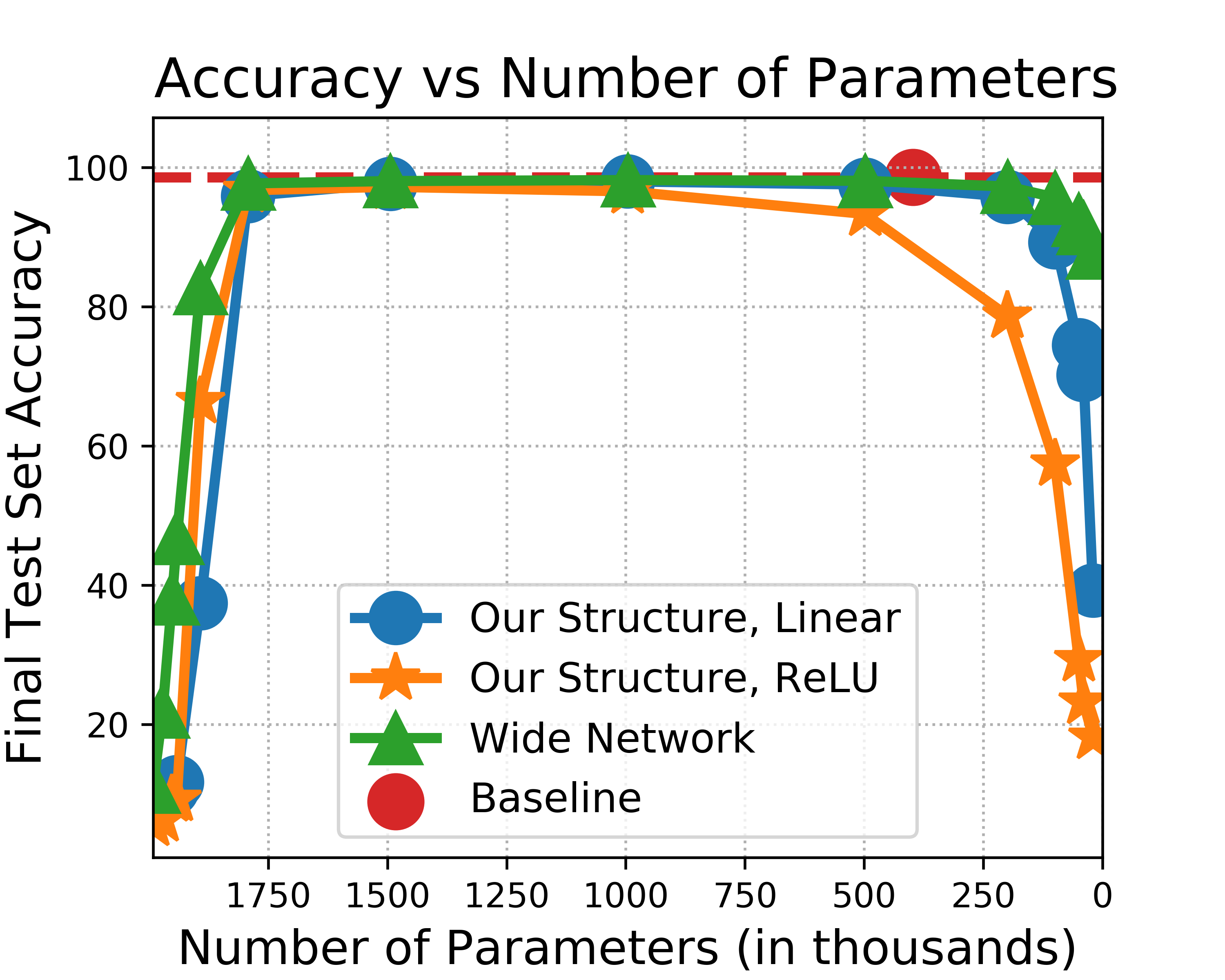
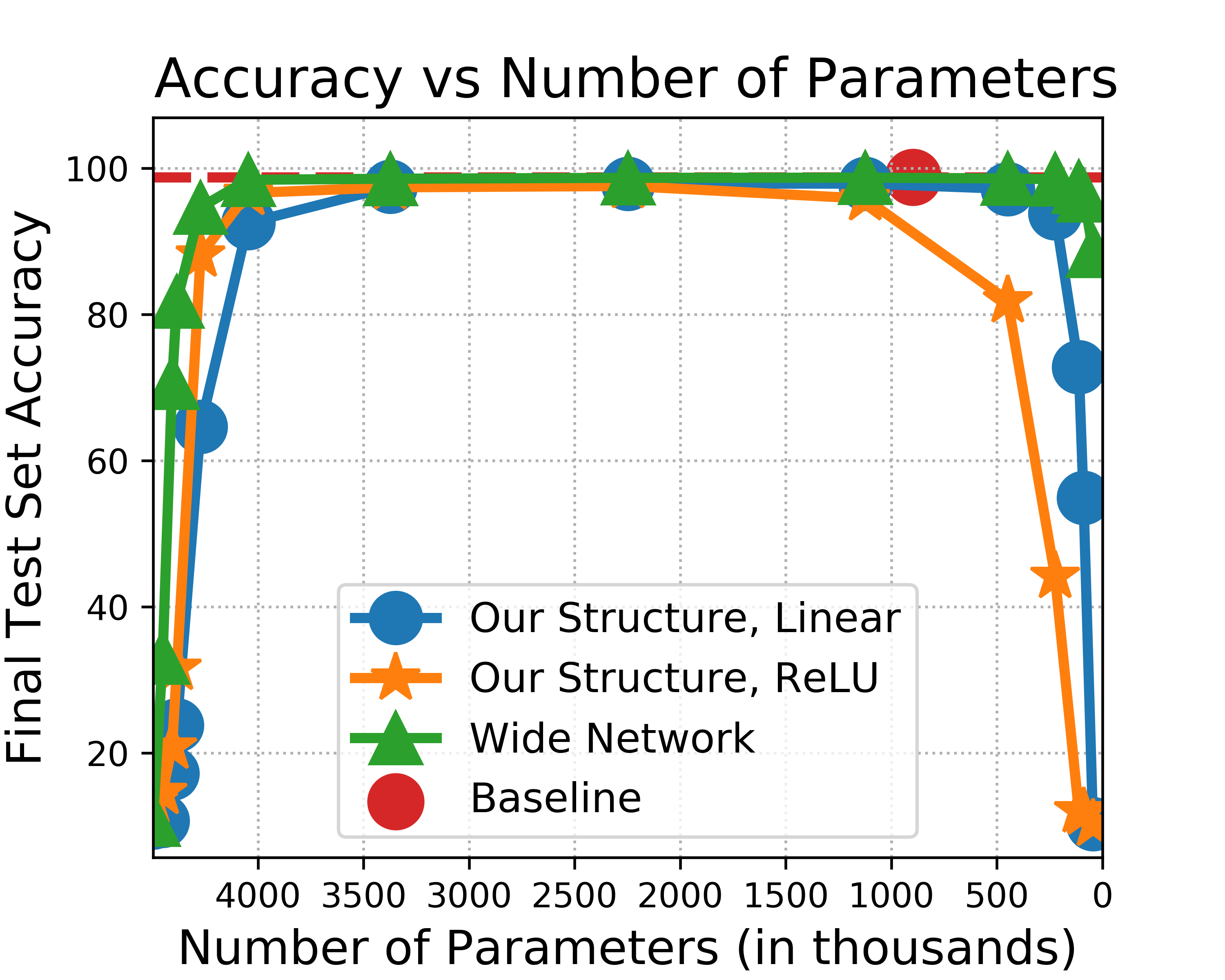
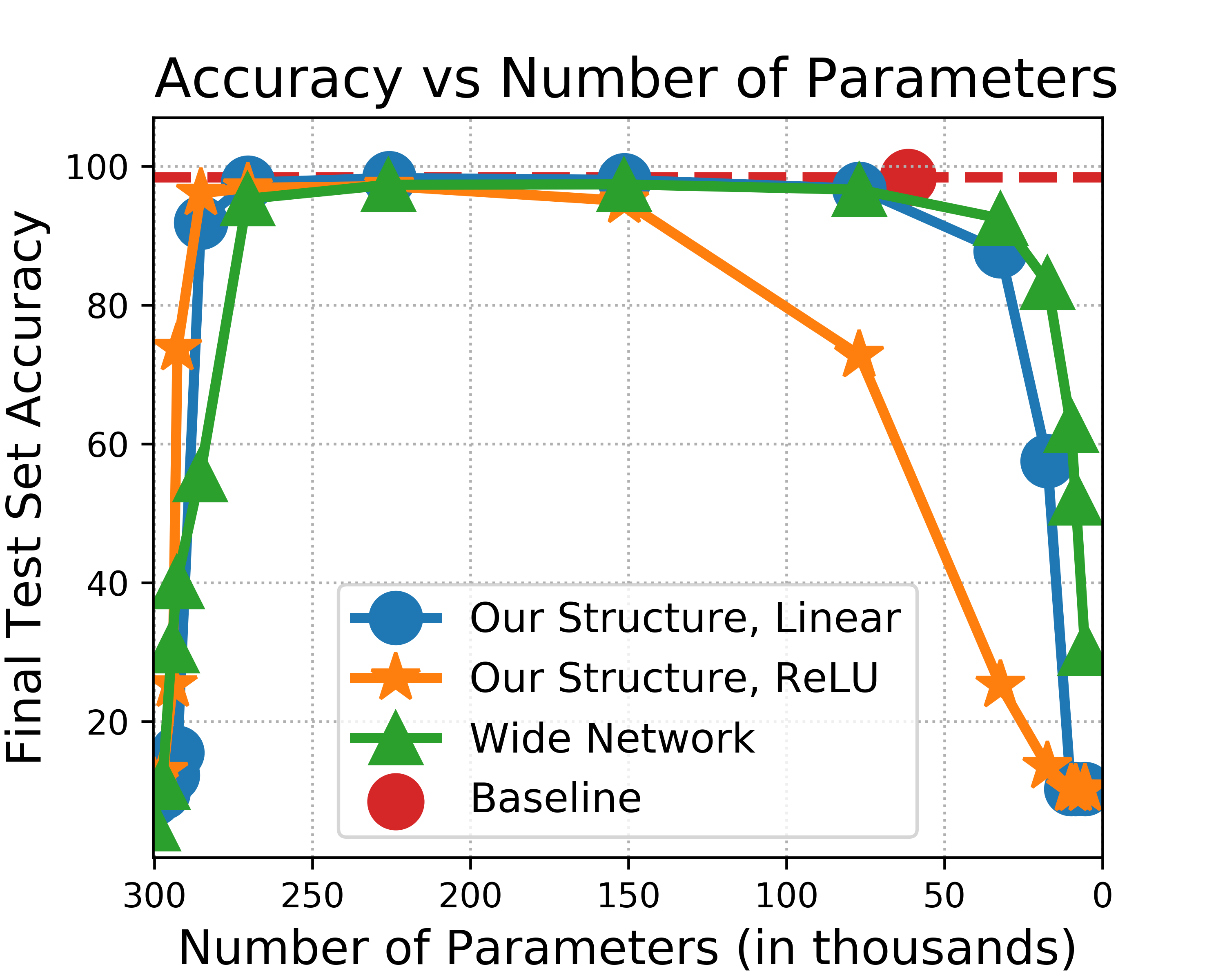
For networks that use our structure and for baseline networks, the argument --hidden-size works as one might expect: it specifies the number of hidden nodes in the fully connected layers of a network. There are two exceptions to this rule: (1) LeNet5 architectures have a predetermined number of hidden nodes based on the literature, so --hidden-size is ignored. (2) When pruning a wide network, such as "WideTwoLayerFC" (wide two-layer fully connected network), the number of hidden nodes in the architecture is calculated based off the value specified by --hidden-size and --redundancy. The the number hidden nodes are calculated this way so that the number of parameters in a wide network approximately match the number of parameters in a network that uses our structure. For example, if a "RedTwoLayerFC" (our network) is defined for --hidden-size 500 and --redundancy 5, then defining a "WideTwoLayerFC" with --hidden-size 500 and --redundancy 5 will prune a wide network with the approximately the same number of parameters as the "RedTwoLayerFC" network.
-
To avoid confusion, the sparsity argument has the following interpretation: a sparsity of 0 means "no sparsity" (i.e. "keep all the weights") and a sparsity of 1 means "complete sparsity" (i.e. "prune all the weights"). By this convention, a sparsity of 0.75 means "keep 25% of the weights."
In the pruning directory, there are three bash scripts for our experiments: (1) base.sh contains all the commands for our baseline network results, (2) fc.sh contains all the commands for two- and four-layer fully connected networks that use our redundant structure and the widened networks, and (3) lenet5.sh contains all the commands for our implementing our pruned redundant structure and the wide fully connected layers on LeNet5.
| Model | Inital Params | Remaining Params | Relative Size to Target After Pruning | MNIST Accuracy |
|---|---|---|---|---|
| Target Two-Layer FC | 397k | 397k | 1 (not pruned) | 97.19% |
| Pruned Two-Layer FC | 8.34M | 3.73M | 9.39 | 97.19% |
We thank Eddie Xiong for identifying a small bug in our code.
approx_test_acc = utils.test(model, device, criterion, test_loader, args.batch_size)on line 207 of subset-sum/main.py has been updated to
approx_test_acc = utils.test(approx_model, device, criterion, test_loader, args.batch_size)