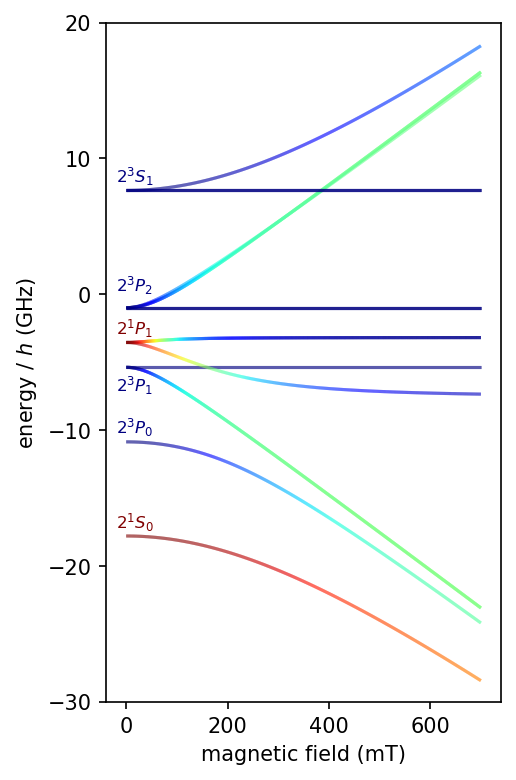
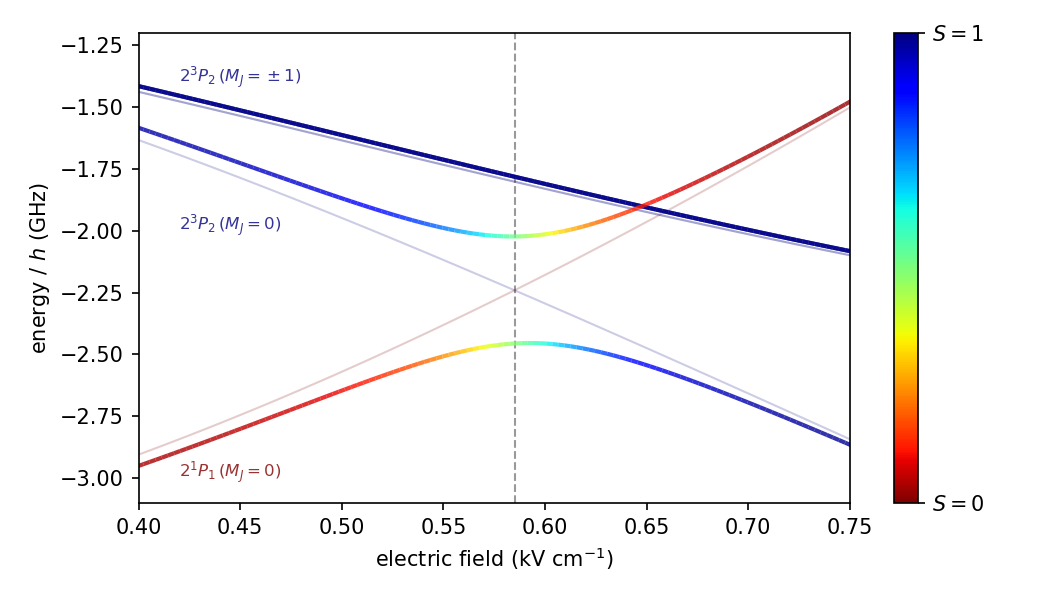
Positronium in parallel electric and magnetic fields.
Fine structure is included to first order using the formula given on page 117 of
Quantum Mechanics of One- And Two-Electron Atomsby Hans a. Bethe and Edwin E. SalpeterISBN 978-1-61427-622-7
with higher order terms for the S and P states from
A. Czarnecki, K. Melnikov, and A. Yelkhovsky, Phys. Rev. A 59, 4316 (1999)
The Stark and Zeeman matrices are constructed using the equations given in:
A. M. Alonso et al., Phys. Rev. A 93, 012506 (2016)
Radial wavefunctions are obtained using the Numerov method, as described by:
M. L. Zimmerman et al., Phys. Rev. A 20, 2251 (1979)
python 3.8+
The main requirements can be installed with conda:
conda install numpy scipy sympy tqdmOptional (speed up high-n calculations): Build and install numerov.
Some of the example notebooks use smtools.
Finally, clone the souce code and then install the package using setuptools.
git clone https://github.com/ad3ller/pypositronium
cd ./pypositronium
python setup.py installBasis is a list of instances of the dataclass State.
>>> from pyps import Basis, Hamiltonian
>>> basis = Basis.build(n_values=range(1, 4))
>>> print(f'number of basis states: {basis.num_states}')
number of basis states: 56
>>> # e.g., the 10th element of the basis set
>>> basis[10]
State(n=2, L=1, S=0, J=1, MJ=0)
>>> # ket notation
>>> print(basis[10])
❘ 2 1 0 1 0 ⟩
The Hamiltonian class is initialised using a basis.
>>> # initialize
>>> H = Hamiltonian(basis)
Calculate the eigenvalues in applied fields.
>>> electric_field = 10.1 # [V / m]
>>> magnetic_field = 0.1 # [T]
>>> en = H.eigenenergies(electric_field, magnetic_field, units="eV")
>>> print(en[:5])
[-6.80332213 -6.8024767 -6.8024767 -6.80247654 -1.70078788]
The methods stark_map() and zeeman_map() calculate the energy eigenvalues for a range of electric or magnetic fields.
See the notebooks for examples.
This code has not been tested extensively, although several published calculations have been reproduced.
S. M. Curry, Phys. Rev. A, 7 (2), 447 (1973) https://dx.doi.org/10.1103/PhysRevA.7.447
A. M. Alonso et al., Phys. Rev. A, 93, 012506 (2016) https://dx.doi.org/10.1103/PhysRevA.93.012506
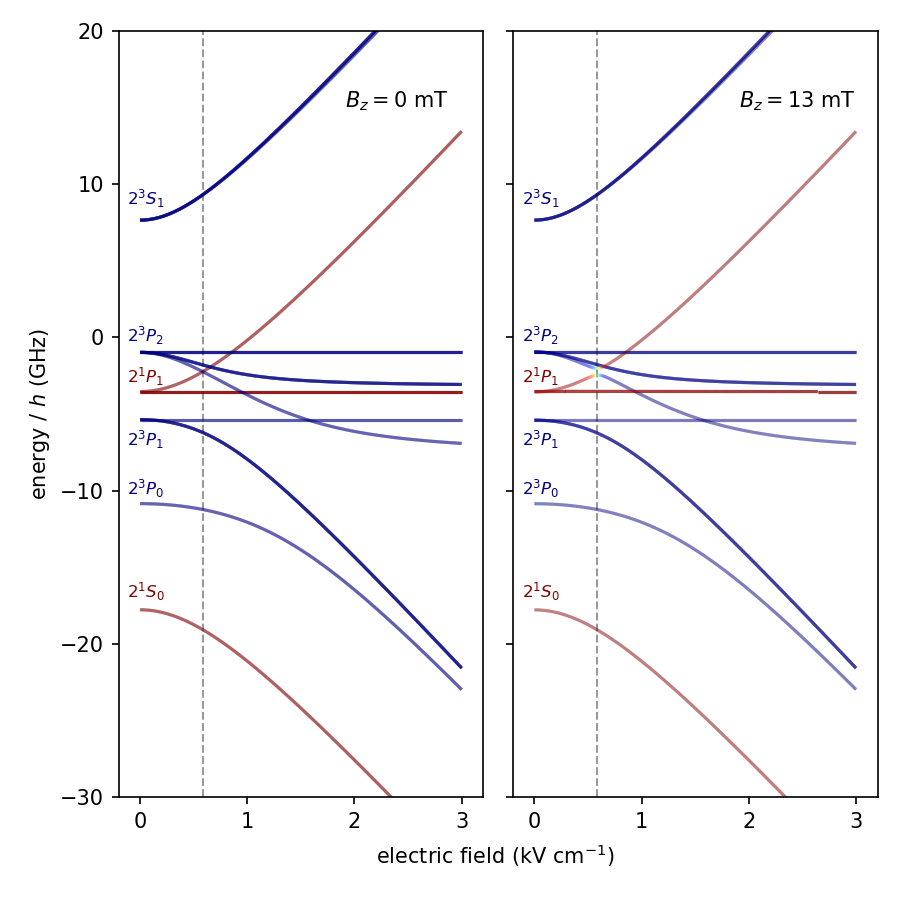
Fig. 6 a) & b) Dependence of the relative energies of all n=2 eigenstates in Ps on electric-field strength (a) in the absence of a magnetic field and (b) in a parallel magnetic field of B=130 G.
G. Dufour et al., Adv. High En. Phys., 2015, 379642 (2015) https://dx.doi.org/10.1155/2015/379642