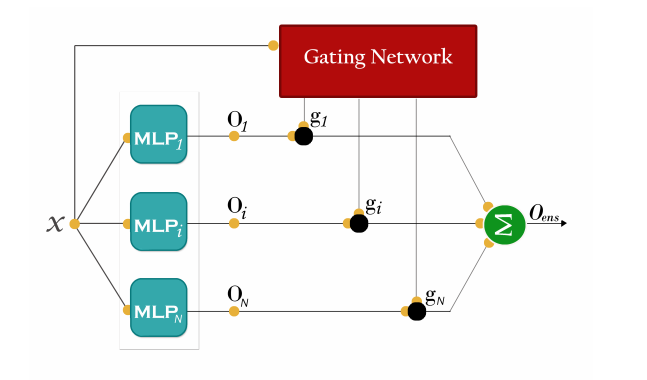
/MixtureOfExperts

Master Thesis. Code written in python. (Keras with Tensorflow backend)

Primary LanguagePythonMIT LicenseMIT

Mixture Of Deep Experts (MoDE)

Mixture of Experts (MoE) is a classical architecture for ensembles where each member is specialised in a given part of the input space or its expertise area. Working in this manner, we aim to specialise the experts on smaller problems, solving the original problem through some type of divide and conquer approach.

My master thesis report can be found here. MoE

Reproducing Collabert et al.

In the paper the author proposes and new approch to scale SVM (almost linear time) as the number of examples increase. SVMs dont scale as the number of examples incerease.

  • Benchmark dataset : Forest
  • Change to binary classification problem
  • Parameter of the kernel is chosen by cross validation
  • Cost function mean square error
  • Termination Condition : Validation Error goes up or Number of iterations
  • Configuration
  • Notebook
  • Code
  • Grid Search Results
SNo. Experiment Train Error Test Error Seq Par Comments
1 One MLP 11.72 14.43 13
2 One SVM 9.85 11.50 25
3 Unifrom SVM 16.98 17.65 15 10
4 Gater 4.94 9.54 140 64 Seq has verbose info, timing might be longer as it has verbose info
5 Gater MLP 17.27 17.66 137

Loss Curves Expert Improvement

Multiclass MLPs

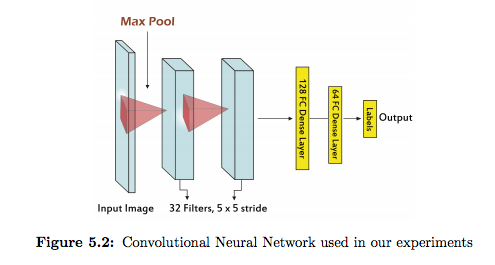
Now we replace our experts with MLP. We use a modified version of LeNet as described below.

LeNet 5

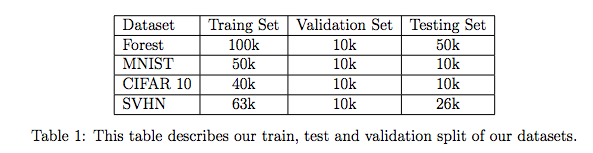
Datasets

Dataset used in our experiments can be seen below.

Data Set

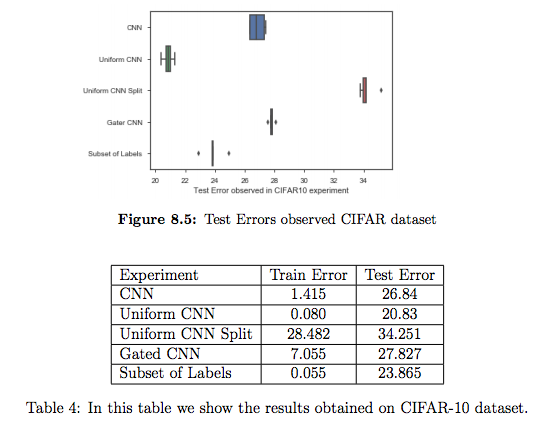
Results for CIFAR10

We consider Uniform CNN split as our baseline since since each expert gets 1/10 of the data. Uniform CNN as our gold standard as all expoers get all the data . Our MOE do suprising well on our data set even when these expert only recieve 1/10 of the data.

Cifar 10

Conclusion

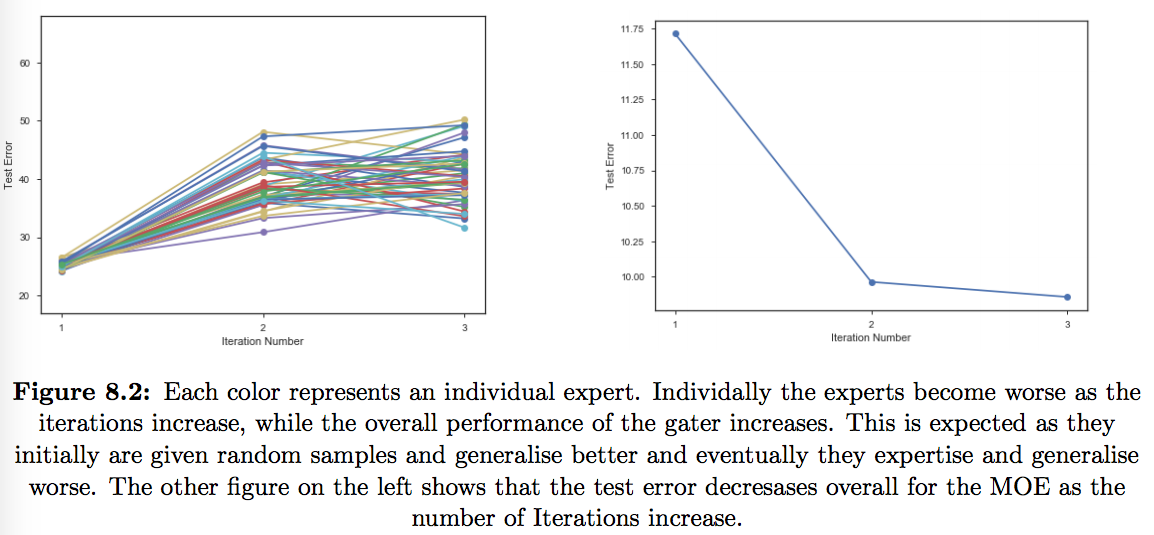
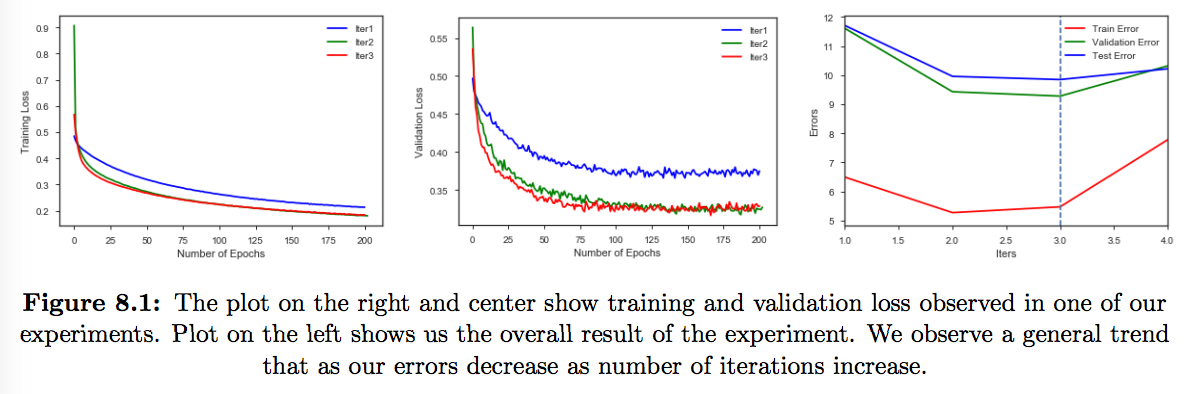
We already highlighted the need for more data to train experts. For MLP as experts we observed convergence within 3 iterations mostly. Also Plot 8.3 showed us there is almost a linear decrease in error as the number of training observations increase. Despite these issues we observe that our MoE and subset of labels have a comparable performance to uniform ensemble of CNN trained on complete data. Subset of labels does a better job than MoE in all the experiments because of the advantage of having more data.