Poincare Embeddings
Paper: Poincaré Embeddings for Learning Hierarchical Representations, 2017, by Facebook AI Research
We used gensim to train and infer our model. They provide awesome, easy-to-use APIs.
Tested code on system with following requirements:
- Python 3.6.5
- Gensim 3.4.0
- Plotly 2.5.1
Concept
Poincare embeddings are a method to learn vector representations of nodes in a graph. The input data is of the form of a list of relations (edges) between nodes, and the model tries to learn representations such that the vectors for the nodes accurately represent the distances between them.
The learnt embeddings capture notions of both hierarchy and similarity:
- Similarity by placing connected nodes close to each other and unconnected nodes far from each other.
- Hierarchy by placing nodes higher in hierarchy near origin and lower hierarchy nodes farther from origin.
The model achieves this by defining a loss function that penalises low distances between unconnected nodes and high distances between connected nodes, and then training over the list of connected nodes, along with randomly sampled negative examples, using gradient descent. Main innovation in these embeddings is that they are learnt in Hyperbolic space, as supposed to commonly used Euclidean space. The reason presented for this is that hyperbolic spaces are more suitable for capturing hierarchical relationship inherently present in graph. Embedding space while accurately preserving the distance between the nodes usually requires large number of dimensions.
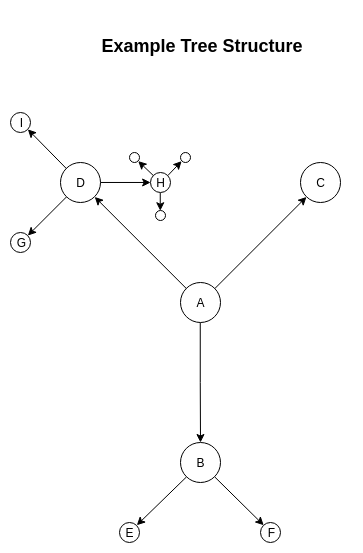
Here, the positions of nodes represent the positions of their vectors in 2-D euclidean space. Ideally, the distances between the vectors for nodes (A, D) should be the same as that between (D, H) and as that between H and its child nodes. Similarly, all the child nodes of H must be equally far away from node A. It becomes progressively hard to accurately preserve these distances in Euclidean space as the degree and depth of the tree grows larger. Hierarchical structures may also have cross-connections (effectively a directed graph), making this harder.
There is no representation of this simple tree in 2-dimensional Euclidean space which can reflect these distances correctly. This can be solved by adding more dimensions, but this becomes computationally infeasible as the number of required dimensions grows exponentially. Hyperbolic space is a metric space in which distances aren't straight lines - they are curves, and this allows such tree-like hierarchical structures to have a representation that captures the distances more accurately even in low dimensions.