Alejandro F Queiruga Lawrence Berkeley Lab 2015-2018
Cornflakes and popcorn are a new general purpose scientific package. It's designed to enable super-quick design of standard scientific codes with a flexible architecture suitable for both prototyping and deployable code. It supports the Scipy backend for interactively designing problems, inspecting matrices, etc., and then the same code can be used with a PETSc or LIS backend for high performance execution. Cornflakes contains the methods for assembling vectors and matrices from the kernels created by the accompanying Domain Specific Language popcorn. In that sense, cornflakes is the runtime to the popcorn DSL. The popcorn repository can be found at https://github.com/afqueiruga/popcorn.
Computational science codes are often broken down into repetitive applications of a kernel to a small chunk of data, e.g., a finite difference stencil applied nine nodes. Cornflakes abstracts the organization of the individual operators into a hypergraph. Each hyperedge of the graph represents one instance of applying the kernel calculation to the data.
Every hypervertex in the graph represents a location with associated data., e.g., the fields values on the finite difference grid points. The edge is the set of vertices containing data required to calculate the kernel. The value of the hypervertex is used to index into a global vector using a DofMap for each of the arguments of the kernels; e.g. vertex 2000 maps to degrees of freedom {6000,6001,6002} in the global vector. A large class of computations can be described by this abstraction, such as
- Finite Element meshes: the edge is an element
- Finite difference grids: the edge is a stencil
- Particle methods: the edge is a neighbor list
Or, in pictures, comparing each of those typical ideas on the left to the abstract hypergraph on the right,
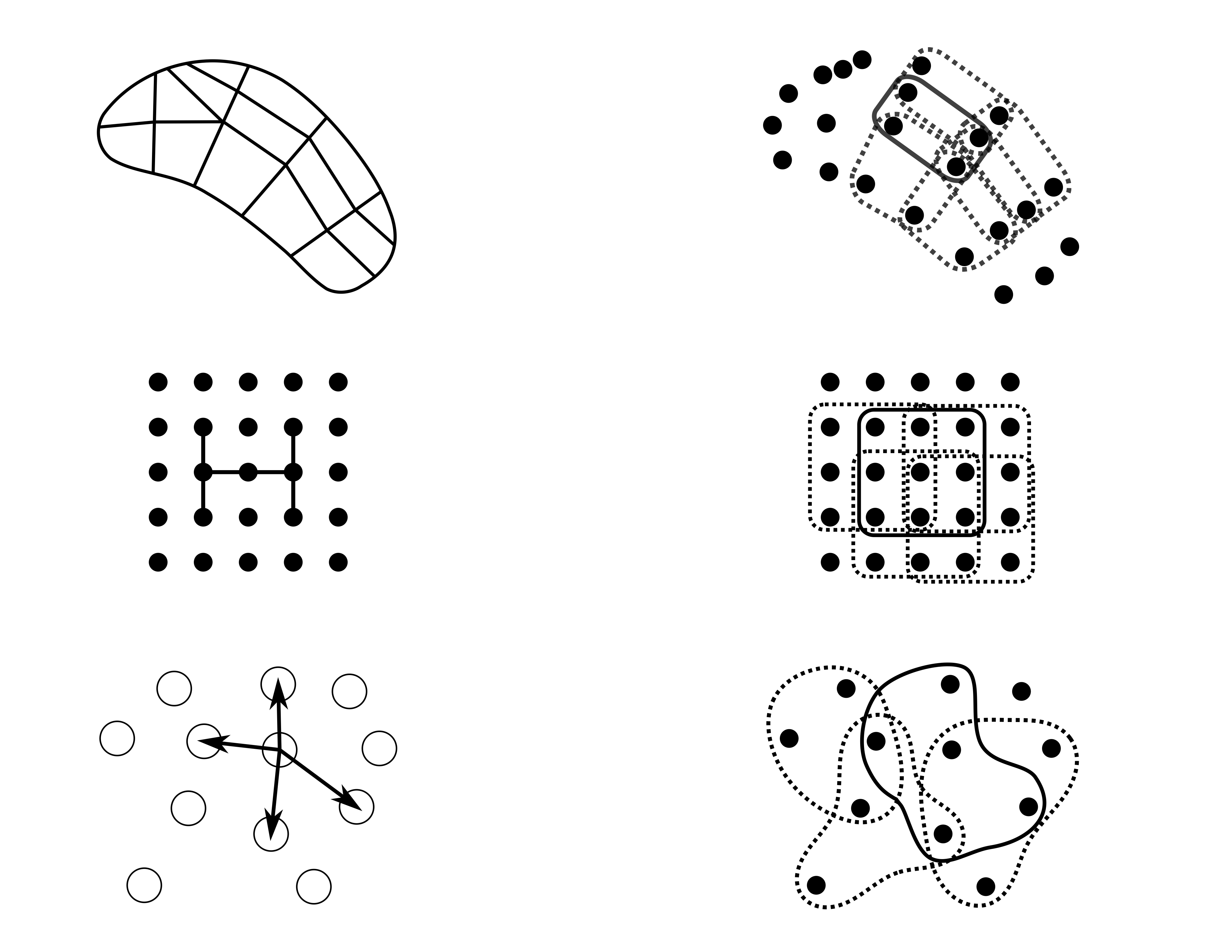The result of each edge computation is a contribution to the global system whose local results are put together in the "big A" assembly:
The
Assemble and solutions of the resulting system of equations.
Cornflakes also includes helpers for forming graphs by loading from a finite element mesh or building a
neighbor list for a particle cloud, and writing out data to VTK or silo files.
Cornflakes is designed to be run in parallel, but, like many things, I haven't gotten to that part yet. (I might just rewrite it all in Julia first.)
The architecture is designed to force data locality and map-apply operations upon the developer's thought process.
assemble() was running with OpenMP, but it wasn't updated.
The popcorn DSL is agnostic to the target processor, and the architecture is designed with GPU execution in mind.
The current project goal is to write a PETSc backend for the hypergraph types and manage ghost zones and distributed matrices through the Vec and Mat types automatically.
The hypergraph of the problem is used to distribute the computations in parallel by assigning edges to processors using the overlap of vertices to minimize the communication.
The parallel vectors can then be distributed by figuring out where vertices ended up.
However, the architecture is still in flux and I cannot commit the manhours to actually implementing any of these parallel models yet.
What does that mean? Well, this is a very simple kernel:
from popcorn import *
Vector = DofSpace(2,0,2) # vector on each vertex
Param = DofSpace(1,-1) # global
i_x = Input('x',Vector) # original position
i_y = Input('y',Vector) # new position
i_k = Input('k',Param) # stiffness
x0,x1 = i_x.Vertex_Split()
y0,y1 = i_y.Vertex_Split()
norm = lambda a : sqrt( (a.T*a)[0,0] )
f = i_k[0] * (norm(y0-y1)-norm(x0-x1))/(norm(y0-y1) * (y1-y0)
R = Matrix([f,-f])
K = R.jacobian(i_y) # <---- Take a symbolic derivative!
o_R = Output('R',[Vector],1)
o_K = Output('K',[Vector],2)
Kernel("spring_force",
listing=[
Asgn(o_R,R,'='),
Asgn(o_K,K,'=')
])
Husk('spring')and this is a script that uses it to solve problem:
import cornflakes as cf
import numpy as np
import husk_spring
dm_scalar = cf.Dofmap_Strided(1)
dm_vector = cf.Dofmap_Strided(2)
x = cf.PP.init_grid(10,10,[0,0],[1,0],[0,1])
y = x.copy()
H = cf.Graphers.Build_Pair_Graph(x,0.2)
data = {
'x':(x,dm_vector),
'y':(y,dm_vector),
'k':(np.array([1.0]),dm_scalar)
}
K,R = cf.Assemble2(husk_spring.kernel_spring_force,
H,data,
{'R':(dm_vector,),'K':(dm_vector,)},
ndof=x.size)
marked_bot = cf.select_nodes(x, lambda a:a[1]<0.0001)
bcdofs = dm_vector.Get_List(marked_bot)
bcvals = np.zeros(bcdofs.shape,dtype=np.double)
cf.Apply_BC(bcdofs,bcvals, K,R)
marked_top = cf.select_nodes(x, lambda a:a[1]>1.0-0.0001)
loaddofs = dm_vector.Get_List(marked_top).reshape(len(marked_top),2)[:,1] # Just the y's
R[loaddofs] -= 0.5
import scipy.sparse.linalg as splin
u = splin.spsolve(K,R)
y -= u.reshape(y.shape)That's all the code it takes to solve (one Newton iteration) of a nonlinear spring network.
See the example notebook for a walk through: /examples/spring_example.ipynb
More examples can be found in the examples directory. Those are split up into two files, the popcorn specification and the cornflakes script.
The computational kernels (like "spring_force") are the building blocks of
scientific programs. Popcorn solves the problem of both doing the mathematical derivations
and writing the code for complex equations. Note how above we just took the tangent
of the residual in one line. We can even make
Cornflakes assembles those computational kernels into the things we need, systems of
equations. Cornflakes does not tell you how to layout data nor does it help you
solve the systems of equations. (That's PETSc's job.) The data layout is seperate from the
kernel implementation. It is possible to reuse the same popcorn kernels and change the
Dofmap objects to assemble kernels from different projects with different numerical
methods into the same linear system, with an interwoven layout for cache optimization and
fill-reducing ordering.
Cornflakes also does not care about the underlying data types.
The CFData and CFMat objects wrap numpy, scipy, PETSc, and LIS objects, and are
extensible. At the Python level, it is possible to seemlessly use Numpy and Scipy types.
These are the current guiding points to the architecture design:
- The user must retain control of main.
- Agnostic to how the kernel was written. It just has to have the kernel struct. The first DSL was already replaced (kerngen).
- The code generation should run pre-compile time, not just-in-time. It gets expensive. Some of my kernels take 5 minutes to run. The production code should be given already compiled shared object files.
The main idiom is that a single calculation is at a minimum two files:
- method_pop.py: the popcron file specifying one or more kernels
- simulation.py: the actual calculation that imports the husk, uses cornflakes to describe a hypergraph and assemble a result by applying the kernels to the hypergraph, and uses another library to solve the matrices of your choice.
Cornflakes is heavily inspired by FEniCS. (If you just need to do FEM, use FEniCS! Cornflakes isn't ready for you.) My dissertation involved extensive modifications to FEniCS in both Dolphin and FFC to express the multiphysics, nonlinear contacts between elements. I managed to express the integrals in the DSL but saw the limitations to express anything further. With dolphin, I had to copy-and-paste a lot of code, and felt that I could make it more general. I was further working on coupling Discrete Elements to FEniCS for particle-laden flow, but I realized there must be a better way.
Cornflakes and popcorn were first written to perform the studies in "Numerical experiments on the convergence properties of state-based peridynamic laws...", where I needed a new DSL system to describe, automatically derive, and differentiate general Peridynamic calculations.
So far I've cornflakes and popcorn to program:
- Finite Elements
- Peridynamics
- Bonded Particles
- Reproducing Kernel Particle Method
- Fully coupled Peridynamics + 2D FEM + 1D dynamically mesh FEM, all in cornflakes
- FEM in cornflakes coupled to an externally linked finite difference code
The design of cornflakes is similar to the following libraries:
- FEniCS - difficult to generalize past finite elements
- MOOSE - No control over main; no DSL
- PyOp2 - Assembler only. It seems great, but it was developed in parallel to cornflakes! It's only been used for FEniCS kernels, and seems married to the interpretation as a physical mesh.
Tensorflow has a similar idea to describing calculations as a graph, but the graph entities represent different things. In cornflakes, each Hypergraph represents kernel calculations that can happen in parallel, with the graph connectivity representing how small bits of data overlap. The purpose of the cornflakes description is to facilitate communication-minimizing graph partitioning across HPC systems. E.g., the use case is to distribute tens of millions of calculations representing elements of a mesh across an HPC system, which will have to be evaluated millions of times. In TensorFlow, the graph nodes represent larger computations that are chained together in a Directed Acyclic Graph, whose edges describes the interdependencies for the ordering for the calculations. The concepts are not mutually exclusive. On another front, I'm interested in writing a TensorFlow op for calling cornflakes assemblies (to train codes), and an cornflakes assemble interface for calling TensorFlow models (to use those codes.)
The following packages are the minimum: gcc cmake python numpy scipy swig gsl.
Just install them with your package manager.
Cornflakes currently only runs in Python 2.7, a design decision due to other interacting libraries that were still on 2.7 when development started.
(Everything is slowly getting ported to Python 3, but the Swig interface is a hassle!)
Popcorn should be installed in the same path. Vtk and silo files are the primary output format. PETSc and LIS support is optional.
The easiest way is to just pull the docker image, which is automatically built by the docker cloud:
docker pull afqu/cornflakesThen, run it with
docker run -ti -v `pwd`:/home/user afqu/cornflakesThe directory superbuild contains another CMakeLists.txt, which will automatically install and download LIS, PETSc, and popcorn, and install them alongisde cornflakes. This makes it easy to keep environments the same for the multiply linked environments. I use the superbuild provided by cornflakes to derive the superbuild for a much larger suite that is built upon cornflakes, as well as to manage the Dockerfile.
Cornflakes uses cmake to compile. The wrappers to LIS and PETSc are optional; use the options in the configuration to point cmake to their install locations. A superbuild and a dockerfile is coming soon. This is the general build process:
- mkdir build
- cd build
- ccmake /path/to/cornflakes/repository
- set CMAKE_INSTALL_PREFIX to somewhere local
- Set USE_LIS or USE_PETSC
- make
- make test
- make install
Cornflakes installs an env.bash.conf and an env.csh.conf to the install prefix.
Source the one corresponding to your terminal to load cornflakes into the path.
After installing cornflakes, use the setup.py in popcorn install it in the prefix (stored in the environment variable $CORNFLAKES_DIR.)
Things on OSX are tricky. You'll need to know where to link things. Here is how to determine the locations for a macports based system:
- set CMAKE_C_COMPILER and CMAKE_CXX_COMPILER gcc-mp-5
- set SWIG_EXECUTABLE: /opt/local/bin/swig
- Set EXTRA_INCLUDES: port contents numpy | grep include
- Set PYTHON_INCLUDE_DIR port contents python27 | grep include
- Set PYTHON_LIBRARY port contents python27 | grep libpython2.7
The macports and homebrew toolchains will be included with the aforementioned superbuild.
Copyright (C) Alejandro Francisco Queiruga, 2015-2018 Lawrence Berkeley National Lab
Cornflakes is released under version 3 of the GNU Lesser General Public License, as per LICENSE.txt.
Cite this repository if you refer to the code or use it.
Initial development was primary supported by Laboratory Directed Research and Development (LDRD) funding from Berkeley Lab, provided by the Director, Office of Science, of the U.S. Department of Energy. Continuous development on cornflakes/popcorn occurs to support various projects at Lawrence Berkeley National Lab.