En este repositorio se recogen ejemplos prácticos de aprendizaje computacional realizados
siguiendo la lectura del libro Python Machine Learning de Sebastian Raschka y Vahid Mirjalili.
-
Objetivo - Aprender un modelo a partir de datos de entrenamiento etiquetados, que permite hacer predicciones de futuro.
-
Ejemplos - Filtro de correo no deseado. Este es un ejemplo de tarea de clasificación con asignación de etiquetas. Otro ejemplo podría ser de este tipo de aprendizaje la regresión, donde el valor predicho puede ser un valor continuo.
-
Objetivo - Desarrollar un agente que mejore su rendimiento basado en interacciones con el entorno. En este caso, durante el periodo de aprendizaje los resultados no se contrastan con la etiqueta o el valor correcto de los datos de entrada, sino con una función de recompensa.
-
Ejemplos - Motor de ajedrez, donde el agente elige entre una serie de movimientos y la recompensa se puede definir como la victoria o la derrota al final del juego.
-
Objetivo - Explorar la estructura de un conjunto de datos de entrada sin etiquetar para extraer información significativa de ellos.
-
Ejemplos - Descubrir grupos de clientes basados en sus intereses con el fin de desarrollar estrategias de marketing.
Algoritmo capaz de optimizar un conjunto de coeficientes de peso en base a los cuales realizar predicciones.
Durante la fase de entrenamiento se utilizan un conjunto de datos de entrada etiquetados. En una serie de iteracioneso o épocas realizadas sobre ellos, llamadas entrenamiento, el algoritmo es capaz de optimizar los pesos.
Esta optimización se realiza obteniendo el producto de los pesos con los valores de entrada, el cual se contrasta con una función escalón en base a la etiqueta de los valores de entrada.
La convergencia sólo está garantizada si las clases son linealmente separables y el rango de aprendizaje es suficientemente pequeño.
La diferencia con respecto al perceptrón reside en que los pesos se actualizan en base a una función de activación lineal (o función objetivo o función de coste), en lugar de hacerlo en base a una función escalón unitario. Minificar el coste de esta función lineal permitirá desarrollar algoritmos más avanzados.
Algunas de las estrategias para disminuir este coste son:
-
Optimizar el rango de aprendizaje - Experimentación con distintos rangos de aprendizaje en contraste con la convergencia y el número de errores obtenido.
-
Descenso de gradiente - Algoritmo de aproximación mediante sucesivas iteraciones.
-
Descenso de gradiente estocástico - Similar al descenso de gradiente, sin embargo la actualización de pesos se realiza de forma incremental para cada muestra de entrenamiento.
-
Escalado de características - Tratamiento de los datos de entrada que favorece la convergencia.
A pesar de su nombre, se trata de un modelo para clasificación, similar a los anteriores modelos.
Es muy similar al modelo Adaline, sin embargo en lugar de utilizar una función de activación lineal para la optimización de pesos, se utiliza una función sigmoide, que se interpreta como la probabilidad de que una muestra pertenezca a una etiqueta determinada.
Una de las ventajas de este modelo es que no sólo es capaz de predecir la etiqueta de la muestra, también la probabilidad de que ésto ocurra. Por este motivo es un módelo popular para predicciones metereológicas o cálculo de probabilidades de que un paciente padezca una enfermedad concreta en función a determinados síntomas.
Puede considerarse como una extensión del Perceptrón. Mientras que el objetivo del Perceptrón es minimizar los errores de clasificación, el objetivo de optimización de este modelo es maximizar el margen o distancia de los límites de decisión.
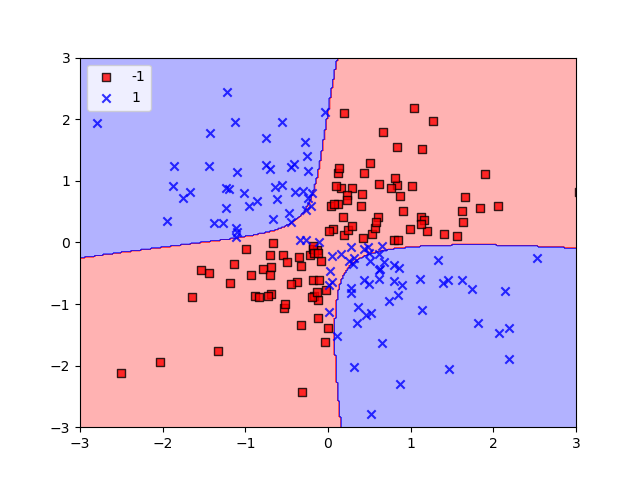
La ventaja de ampliar este margen es que estos modelos tienden a tener un error más bajo en la generalización, allí donde los modelos con márgenes más estrechos son más propensos al sobreajuste (éstos conceptos se desarrollan en el siguiente apartado), como se puede ver en el siguiente ejemplo:
Otro motivo para su utilización es que puede ser fácilmente kernelizada para resolver problemas de clasificación no lineal, como se puede ver en el siguiente ejemplo:
Utilizando el algoritmo de decisión, empezamos por la raíz y dividimos los datos en la característica que resulta en la mayor ganancia de información o IG.
En un proceso iterativo, repetimos este procedimiento de división en cada nodo hijo hasta que las hojas sean puras. Esto producirá un árbol muy profundo que puede provocar sobreajuste, por lo que una buena opción es podar el árbol ajustándolo a una profundidad máxima.
Las medidas de impurezas o criterios de división que normalmente se utilizan en árboles de decisión binarios son:
- Impureza de Gini
- Entropía
- Error de clasificación
Un bosque aleatorio se puede considerar como un conjunto de árboles de decisión. La idea es promediar la decisión de múltiples árboles que individualmente sufren una elevada varianza, para crear un modelo más robusto.
A partir de una muestra aleatoria de tamaño n se crea un árbol de decisión, y así sucesivamente hasta llegar al número total de árboles que componen el bosque. Al tratarse de una muestra aleatoria, existirá una gran diversidad entre los árboles que componen el bosque, y la clasificación se realizará por mayoría de votos.
El único parámetro que debemos tener en cuenta para solucionar problemas de ajuste es el número de árboles. Cuanto más alto es éste número, el rendimiento será mejor a expensas de un mayor coste computacional. En menor medida, otros parámetros a tener en cuenta son el tamaño de la muestra y el número de características a tener en cuenta para cada división.
Se trata de un algoritmo vago, ya que en lugar de obtener una función discriminativa, memoriza el conjunto de datos de entrenamiento.
Su estrategia es elegir una muestra y una distancia, encontrar los k-vecinos más cercanos dentro de esa distancia y asignar una etiqueta a la muestra por mayoría de votos en base a la clasificación de sus vecinos.
La principal ventaja es que carece de coste de entrenamiento y se adapta inmediatamente cuando se recogen nuevos datos de entrenamiento. Sin embargo, el coste computacional crece linealmente con las nuevas muestras y el espacio de almacenamiento puede llegar a ser un problema.
La elección del número de vecinos y de la distancia para obtenerlos será crucial encontrando un buen equilibrio entre el sobreajuste y el subajuste.
En los modelos paramétricos, a partir de un conjunto de datos de entrenamiento obtenemos una función que pueda clasificar nuevos datos sin necesidad del conjunto de datos de entrenamiento original. Algunos ejemplos son:
- Perceptrón
- Regresión logística
- Máquina de vectores de soporte (SVM)
Contrariamente, en los modelos no paramétricos el número de parámetros crece con los datos de entrenamiento, como se puede ver en:
- Árboles de decisión
- Bosques aleatorios
- SVM kernelizada
- K-vecinos más cercanos
El sobreajuste es un problema común en el que un algoritmo funciona bien durante el entrenamiento pero no generaliza correctamente con los datos de prueba. En este caso se dice que el modelo tiene una alta varianza, causada generalmente por un modelo demasiado complejo.
De forma parecida, un modelo puede no ser lo suficientemente complejo para capturar correctamente el patrón en los datos de entrenamiento, provocando una situación de subajuste o underfitting.
Estos problemas se dan en modelos de decisión no lineales, y una estrategia de compensación es la denominada regularización.
Al enfrentarse a un problema no lineal, una de las estrategias para encontrar un modelo que se ajuste adecuadamente es proyectar las características originales hacia un espacio de dimensiones mayores.
Un ejemplo es transformar un conjunto de datos bidimensionales en un nuevo conjunto de características tridimensionales y encontrar un hiperplano lineal que se convierta en un límite de decisión, para volver a proyectar las características en el espacio original.
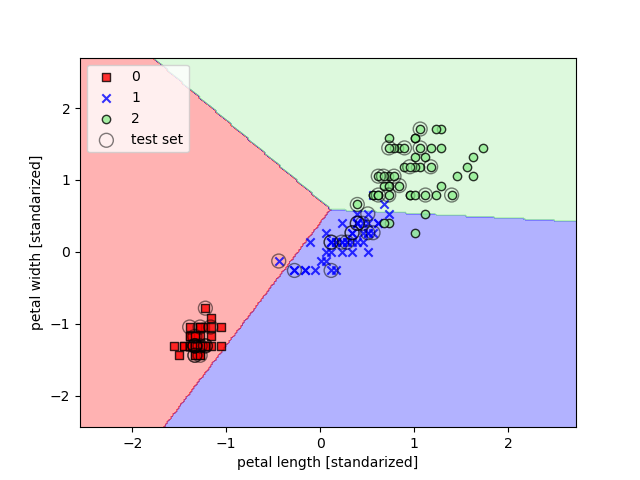
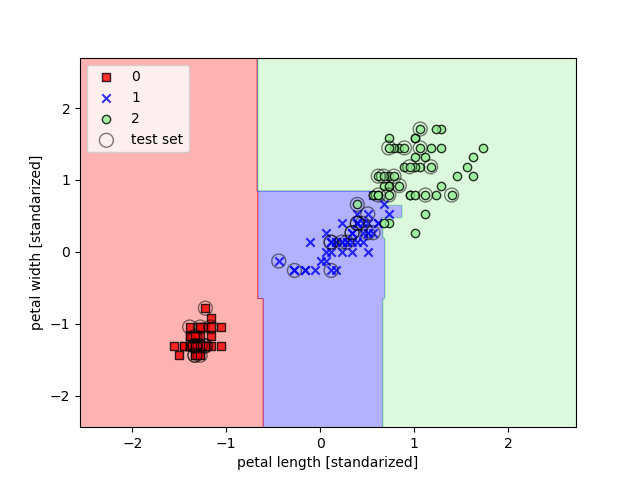
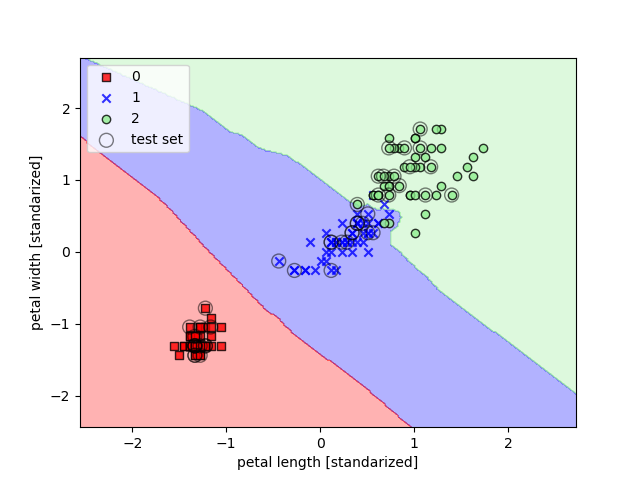
A continuación se muestran dos ejemplos de kernelización para resolver el clásico problema de clasificación de flores
Iris, en el primero, el parámetro gamma o parámetro de corte para la esfera Gaussiana tiene un valor bajo, lo
que genera un modelo de límites más suaves:
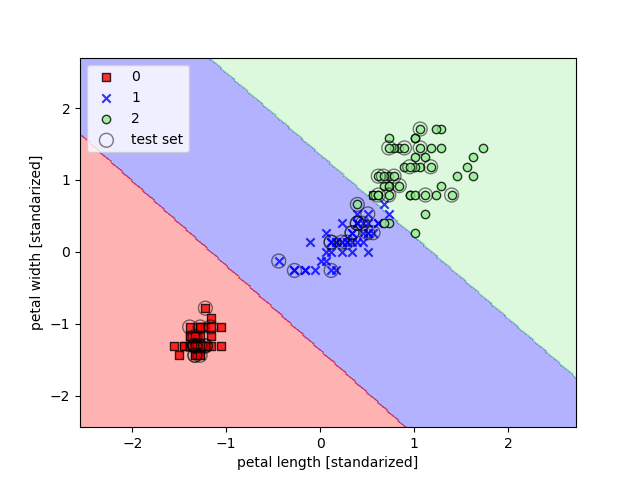
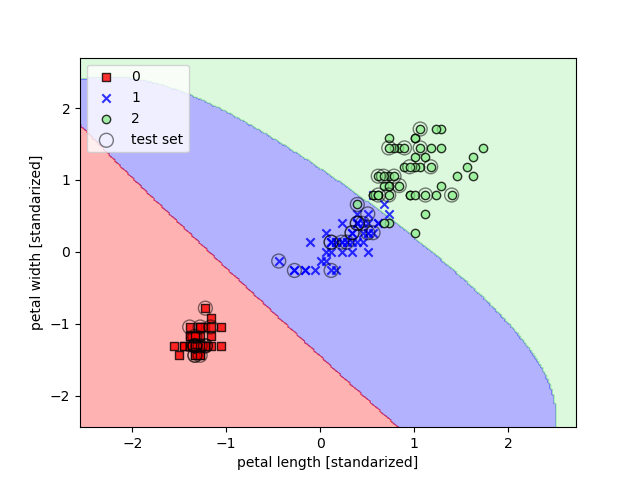
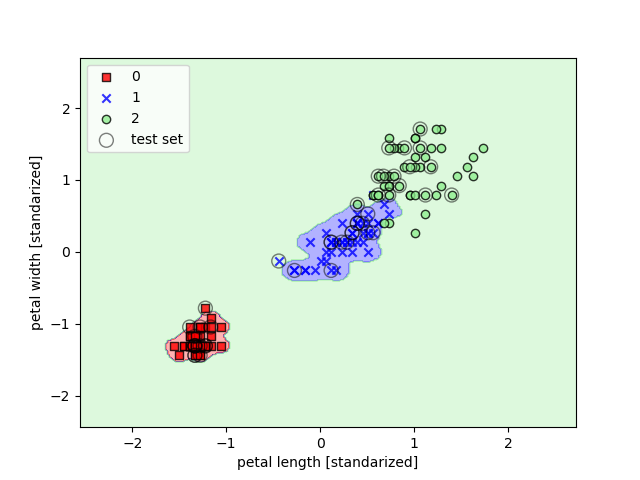
En el segundo ejemplo, este valor es más elevado, con lo que los límites son más ajustados:
La cantidad y calidad de los datos con los que se entrena un algoritmo determinan lo bien que puede aprender. A continuación se describen una serie de técnicas básicas para potenciar estas cualidades en la información manejada.
Algunas muestras pueden carecer de uno o más valores, lo que puede provocar que el algoritmo no pueda manejar estas muestras o bien genere resultados impredecibles. Las opciones para solventar este problema son:
-
Eliminar muestras incompletas - Este enfoque permitirá unos resultados previsibles, sin embargo eliminar demasiadas muestras puede conllevar a resultados poco fiables o a la incapacidad para realizar una buna discriminación entre clases.
-
Imputar valores ausentes - Se utilizan distintas técnicas de interpolación (como la media o el valor más frecuente de una característica concreta) para asignar un valor.
Tanto las características nominales (valores no numéricos sin relación de orden entre ellos) como las ordinales (valores no numéricos con una relación de orden entre ellos) se deberán transformar en valores enteros para poder ser procesados por el algoritmo.
En caso de las características nominales, una simple asignación de números enteros aleatorios a cada uno de los posibles valores podría producir resultados poco óptimos si el algoritmo interpreta que existe una relación de orden entre ellos.
Una solución a este problema es la codificación en caliente, que crea una nueva característica ficticia para cada valor único en la columna de características nominales.
Por lo general no es interesante colocar demasiados datos en el conjunto de prueba, sin embargo, cuanto menos sea el tamaño de este conjunto, menos precisa será la estimación del error de generalización.
Las proporciones que se utilizan con más frecuencia se encuentran dentro del rango 60:40-80:20, sin embargo para grandes conjuntos de datos el rango 90:10-99:1 podría ser adecuado.
Es habitual entrenar al algoritmo con los datos de prueba una vez realizada la primera estimación para mejorar el rendimiento. Sin embargo, si el modelo es demasiado pequeño este rendimiento puede verse devaluado. Otro de los inconvenientes es que sin datos de prueba no se puede evaluar el modelo predictivo final.
Los árboles de decisión y los bosques aleatorios son dos de los pocos algormitmos que no se ven afectados por la escala Los árboles de decisión y los bosques aleatorios son dos de los pocos algormitmos que no se ven afectados por la escala de las características. Sin embargo, la mayoría de ellos tenderán a ajustar sus pesos en torno a aquella característica que se encuentra en una escala mayor, ignorando el resto de características.
Los dos enfoques más importantes en el ajuste de escalas son:
-
Normalización min-max - Reescalado de características en un rango de [0, 1], útil cuando se necesitan valores en un intervalo limitado.
-
Estandarización - Centra las características en torno a una media con una desviación estándar de 1, indicado para algoritmos con descenso de gradiente o para aquellos que inicialicen sus pesos a valores cercanos a 0, como la regresión logística y las SVM.
La tabla siguiente muestra la diferencia entre las dos técnicas de escalado:
| Entrada | Estanzarizada | Normalizada min-max |
|---|---|---|
| 0.0 | -1,46385 | 0.0 |
| 1.0 | -0,87831 | 0.2 |
| 2.0 | -0,29277 | 0.4 |
| 3.0 | 0,29277 | 0.6 |
| 4.0 | 0,87831 | 0.8 |
| 5.0 | 1,46385 | 1.0 |
Cuando un modelo indica problemas de sobreajuste, las soluciones más frecuentes para reducir el error de la generalización son las siguientes:
- Recoger más datos de entrenamiento.
- Introducir una penalización para la complejidad mediante la regularización.
- Elegir un modelo más sencillo con menos parámetros.
- Reducir la dimensionalidad de los datos.
La regularización da como resultado unos valores menos extremos, mientras que con la reducción de dimensionalidad se modificarán las características dando como resultado modelos menos complejos, lo que es especiamente útil en algoritmos que no aceptan regularización.
Dentro de la reducción de dimensionalidad existen dos técnicas muy diferentes. Una es la selección de características, que elimina características en función de su relevancia, y otra es la extracción de características, que comprime las características en lugar de eliminarlas.
Estas soluciones no sólo son aplicables a problemas de sobreajuste, también sirven para reducir la complejidad computacional durante el entrenamiento o minimizar los costes de recopilación de datos en caso de ser requerido.
Un ejemplo de reducción de dimensionalidad es el proceso de selección de características llamado SBS o selección secuencial hacia atrás. Este algoritmo elimina secuencialmente cada una de las características y compara los resultados para determinar cuales de ellas son irrelevantes.
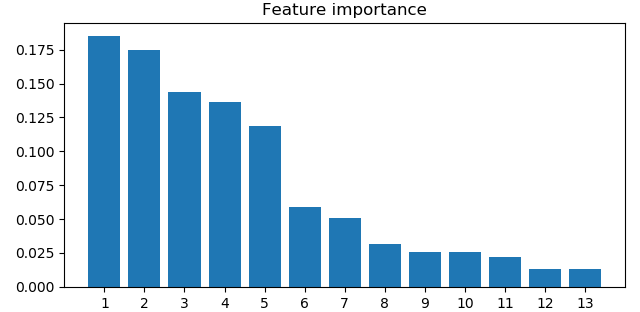
Otro ejemplo es el uso de bosques aleatorios para determinar las características más relevantes en la generalización
de un modelo predictivo y en qué porcentaje afectan a los resultados. Así, en el conjunto de datos Wine, podemos
obtener los siguientes resultados:
A continuación se verán las tres técnicas fundamentales en la extracción de características, que permitirán resumir el contenido informativo de un conjunto de datos en otro de menor dimensión.
Al igual que en la selección de características, estas técnicas serán útiles en la optimización del coste de almacenaje y del coste computacional de datos, además de mejorar el rendimiento productivo del algoritmo.
Además, estas técnicas son especialmente idóneas trabajando con modelos sin regularizar.
Encuentra las direcciones de varianza máxima en datos de alta dimensión y las proyecta en un nuevo subespacio con dimensiones menores o iguales al original.
Encuentra el subespacio de características que optimice la divisibilidad de las clases. A diferencia del anterior, este es un algoritmo supervisado.
Si tratamos con problemas no lineales, las dos alternativas anteriores no serán la mejor elección. Mediante esta técnica proyectaremos el problema en un nuevo espacio donde las clases pasan a ser separables linealmente, para luego aplicar el ACP.
Uno de los pasos clave en la creación de un modelo de aprendizaje automático es estimar su rendimiento en datos no vistos previamente. Un modelo puede sufrir subajuste (sesgo elevado) si es demasiado simple, o sobreajuste (alta varianza) si es demasiado complejo. Para encontrar una compensación sesgo-varianza adecuada se utilizan los siguientes métodos.
Mediante el método de retención, dividimos el conjunto de datos en un conjunto de prueba y otro de entrenamiento. En aplicaciones de aprendizaje automático ajustar y comparar diferentes parámetros para mejorar el rendimiento (este proceso se conoce como selección de modelos). Sin embargo, si reutilizamos el mismo conjunto de datos de prueba, terminará formando parte de los datos de entrenamiento.
Una solución es separar los datos de prueba en tres conjuntos: entrenamiento, validación y prueba. Será sobre el conjunto de validación sobre el que se realizará la selección de modelos.
Un inconveniente de este método es que la estimación del rendimiento puede ser muy sensible a cómo se divida el conjunto de entrenamiento en los subconjuntos de validación y de entrenamiento.
Dividimos aleatoriamente el conjunto de datos de entrenamiento en k iteraciones sin reemplazo, donde k - 1 iteraciones se utilizan para el entrenamiento y una para la evaluación. Este proceso se repite k veces para obtener k modelos y estimaciones de rendimiento. Después se calcula el rendimiento medio de los modelos.
Un buen valor estándar para k es 10, sin embargo, trabajando con conjuntos relativamente pequeños puede ser útil aumentar el número de iteraciones, aunque aumentar este valor provocará un tiempo de ejecución del algoritmo. Por otro lado, para conjuntos grandes de datos un valor de 5 puede ser adecuado y evitar un alto coste computacional.
Dos herramientas pueden ayudar a mejprar el rendimiento de un algoritmo de aprendizaje: curvas de aprendizaje y curvas de validación. La primera permite evaluar si exiten problemas de sobreajuste (alta varianza) o subajuste (sesgo elevado), mientras que la segunda posibilita la corrección de dichos problemas.
Para analizar un texto debemos convertir las palabras en formato numérico. La técnica bolsa de palabras permite representar texto como vectores de características numéricas. Los pasos son los siguientes:
- Crear un vocabulario a partir de un conjunto de documentos.
- Construir el vector de características de cada documento en base a la frecuencia en que cada palabra del vocabulario aparece.
En Python se puede utilizar la clase CountVectorizer para este fin.
Existen un conjunto de palabras que aparecen con frecuencia en los documentos pero que carecen de relevancia o
importancia discriminatoria. Mediante la técnica frecuencia de término - frecuencia inversa de documento se pueden
identificar estas palabras y asociarles un peso menos dentro del vector de características.
Éste sería el primer paso antes de comenzar con el análisis. En el ejemplo asociado a esta documentación, en el que se analizaban críticas de cine obtenidas de una página web, la limpieza de datos ha consistido en eliminar las marcaciones HTML y suprimir un conjunto de palabras identificadas como irrelevantes en cada uno de los documentos.
Este proceso ha de adecuarse a cada caso, en función de los datos con los que se trabajará.
Una vez limpiados los datos se ha de determinar en qué elementos individuales serán descompuestos. Por un lado se ha de definir la longitud en palabras que compondrán estos elementos individuales. Por otro, hay que tener en cuenta la declinación de palabras. El algoritmo de Porter, reduciendo la declinación de cada término a su raíz ha demostrado ser muy efectiva.
Realizados todos estos procesos, sólo queda entrenar un modelo de regresión logística.