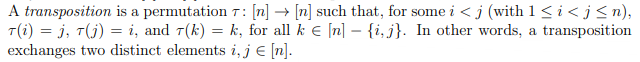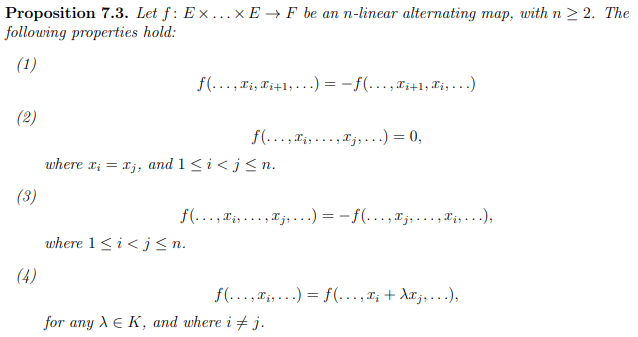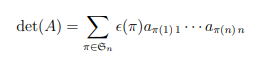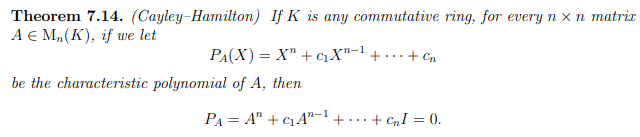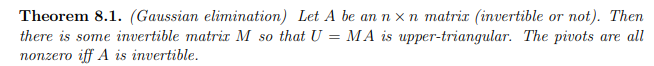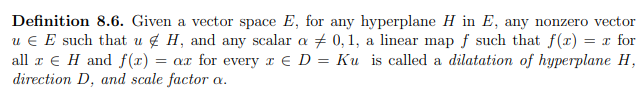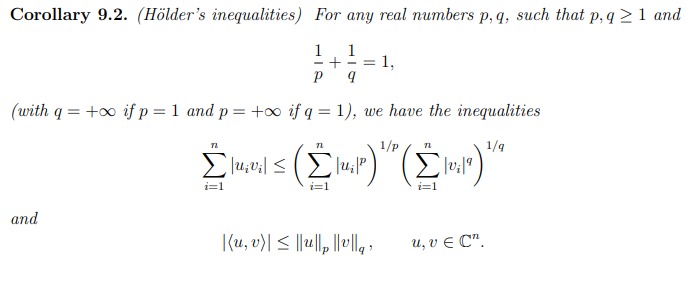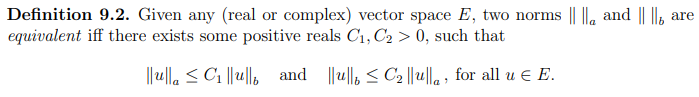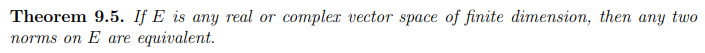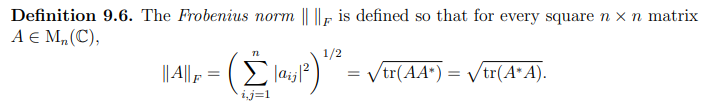Algebra, Topology, Differential Calculus, and Optimization Theory for Computer Science and Machine Learning
Jean Gallier and Jocelyn Quaintance
Contains important notes/definitions/propositions from the book Algebra, Topology, Differential Calculus, and Optimization Theory for Computer Science and Machine Learning Jean Gallier and Jocelyn Quaintance. The book can be found here.
Important chapters (Personally, chapters as indicated by Contents): 2, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 22, 23, 39, 40, 41, 42, 43, 44, 45,46, 47, 48, 49, 50, 51, 52, 54
Table of contents
- Introduction ✅
- Groups, Rings, and Fields ✅
- Vector Spaces, Bases, Linear Maps
- Matrices and Linear Maps
- Haar Bases, Haar Wavelets, Hadamard Matrices
- Direct Sums
- Determinants ✅
- Gaussian Elimination, LU, Cholesky, Echelon Form ✅
- Vector Norms and Matrix Norms ✅
- Iterative Methods for Solving Linear Systems
- The Dual Space and Duality
- Euclidean Spaces
- QR-Decomposition for Arbitrary Matrices
- Hermitian Spaces
- Eigenvectors and Eigenvalues
- Unit Quaternions and Rotations in SO(3)
- Spectral Theorems
- Computing Eigenvalues and Eigenvectors
- Introduction to The Finite Elements Method
- Graphs and Graph Laplacians; Basic Facts
- Spectral Graph Drawing
- Singular Value Decomposition and Polar Form
- Applications of SVD and Pseudo-Inverses
- Basics of Affine Geometry
- Embedding an Affine Space in a Vector Space
- Basics of Projective Geometry
- The Cartan–Dieudonn´e Theorem
- Isometries of Hermitian Spaces
- The Geometry of Bilinear Forms; Witt’s Theorem
- Polynomials, Ideals and PID’s
- Annihilating Polynomials; Primary Decomposition
- UFD’s, Noetherian Rings, Hilbert’s Basis Theorem
- Tensor Algebras
- Exterior Tensor Powers and Exterior Algebras
- Introduction to Modules; Modules over a PID
- Normal Forms; The Rational Canonical Form
- Topology
- A Detour On Fractals
- Differential Calculus ✅TBC
- Extrema of Real-Valued Functions ✅TBC
- Newton’s Method and Its Generalizations ✅TBC
- Quadratic Optimization Problems
- Schur Complements and Applications
- Convex Sets, Cones, H-Polyhedra
- Linear Programs
- The Simplex Algorithm
- Linear Programming and Duality
- Basics of Hilbert Spaces
- General Results of Optimization Theory
- Introduction to Nonlinear Optimization
- Subgradients and Subdifferentials
- Dual Ascent Methods; ADMM
- Ridge Regression and Lasso Regression
- Positive Definite Kernels
- Soft Margin Support Vector Machines
- Total Orthogonal Families in Hilbert Spaces
- Zorn’s Lemma; Some Applications
Introduction
These are just meant to be notes for personal use, you may find them useful. I have very limited background in mathematics, so there may be mistakes here. You will most definitely need to keep the book open on the side as this mentions specific definitions/propositions by reference for brevity.
I may give up on this endeavor at any moment I find better ways to condense knowledge for myself. Honestly, this may be hard to read/understand unless you have a background in mathematics or have read this book atleast roughly.
Groups, Rings, and Fields
Abelian:
A group G is abelian (or commutative) if:
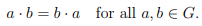
Monoid: Set M with operation MxM -> M and element 'e' satisfying (G1) and (G2) is a monoid. Not necessarily a group.
General Linear Group GL(n, R) or GL(n, C) :
- N x N Invertible with Real/Complex Coefficients
- Group under MatMul
- Identity element In
Special Linear Group SL(n, R) or GL(n, R):
- Sub-group of GL with det(matrix) = 1
Orthogonal Group O(n):
- Set of N x N invertible matrices (Q) with real coefficients
- QQ' = Q'Q = In (Q' is the transpose here.) Special Orthogonal Group SO(n):
- Sub-group of O(n) with Det(Q) = 1
Proposition 2.7: For finite group G, subgroup H of G, orcer of H divides order of G.
Rings
Fields
Characteristic of Field
Vector Spaces, Bases, Linear Maps
Matrices and Linear Maps
Haar Bases, Haar Wavelets, Hadamard Matrices
Direct Sums
Determinants
Permutations
Transpositions
Signature of permutation
Signature of product of transpositions
Properties of Alternating Multilinear Maps:
Important Lemma
Note how:
For the rest of this chapter, K is a commutative ring and when needed a field.
Adjugate and Minor
Invertibility of a Matrix
Determinant of a Linear Map
Cayley-Hamilton Theorem
Permanents
It is a multilinear symmetric form. Refer to book for an execllent interpretation of permanents.
Gaussian Elimination, LU, Cholesky, Echelon Form
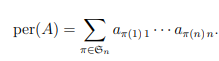
This chapter assumes all vector spaces are over the field R. All results that do not rely on the ordering on R or on taking square roots hold for arbitrary fields.
Read the book for background on Bezier curves and curve interpolation. Gaussian Elimination
- Computing inverse directly is inefficient.
- Solving large linear systems by computing determinants (Cramers formulae) not used.
Solution trivial if A is an upper-triangular matrix. We use Gaussian elimination to iteratively eliminate variables using simple row operations.
Transvections and Dilatations Transvections and Dilatations characterize the linear isomorphisms of a vector space E that leave some vector in some hyperplane fixed. These maps are linear maps represented in some suitable basis by elementary matrices of the form Ei,j;β (Transvections) or Ei,λ (Dilatations).
- Transvections generate the group SL(E)
- Dilatations generate the group GL(E)
Vector Norms and Matrix Norms
Holders Inequalities
For p = 2, it is the standard Cauchy-Schwarz inequality.
Equivalence of norms
Check : Corollary 9.4.
Normal Matrix Mn(C) : AA* = A*A Unitary Matrix Mn(C) : UU* = U*U = I Orthogonal Matrix Mn(R) : QQT = QTQ = I
Characteristic Polynomial, eigenvalues, spectrum and spectral radius.
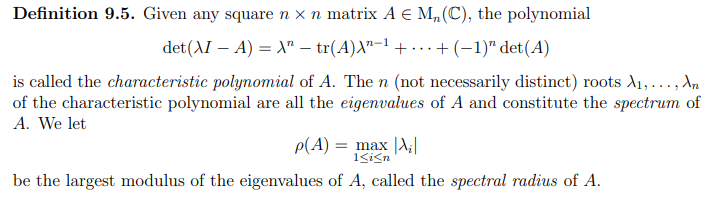
Spectral radius of Mn(C) is always smaller-than or equal to any matrix norm.
Frobenius Norm :
- It is a matrix norm.
- Untarily invariant
Proposition 9.8: It says that every linear map on a finite-dimensional space is bounded, impyling that every linear map on a finite-dimensional space is continuous.
Check Section 9.3 (Subordinate Norms) for another method of obtaining matrix norms.
Condition Number
For its properties, refer to Proposition 9.17.
