To get started: Clone this repository and all its submodule dependencies using:
git clone --recursive https://github.com/alecjacobson/computer-graphics-meshes.gitDo not fork: Clicking "Fork" will create a public repository. If you'd like to use GitHub while you work on your assignment, then mirror this repo as a new private repository: https://stackoverflow.com/questions/10065526/github-how-to-make-a-fork-of-public-repository-private
There are many ways to store a triangle (or polygonal) mesh on the computer. The data-structures have very different complexities in terms of code, memory, and access performance. At the heart of these structures, is the problem of storing the two types of information defining a mesh: the geometry (where are points on the surface located in space) and the connectivity (which points are connected to each other). The connectivity is also sometimes referred to as the topology of the mesh.
The graphics pipeline works
on a per-triangle and per-vertex basis. So the simplest way to store geometry is
a 3D position for each
-th vertex of the mesh. And to store
triangle connectivity as an ordered triplet of indices referencing vertices:
defines a triangle with corners at vertices
,
and
.
Thus, the geometry is stored as a list of
3D vectors: efficiently, we can
put these vectors in the rows of a real-valued matrix
. Likewise,
the connectivity is stored as a list of
triplets: efficiently, we can put
these triplets in the rows of an integer-valued matrix
.
Question: What if we want to store a (pure-)quad mesh?
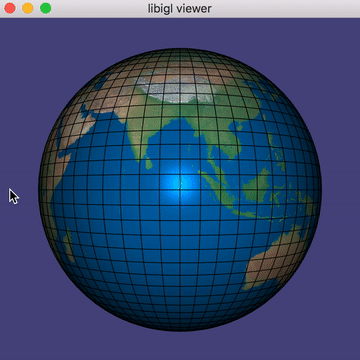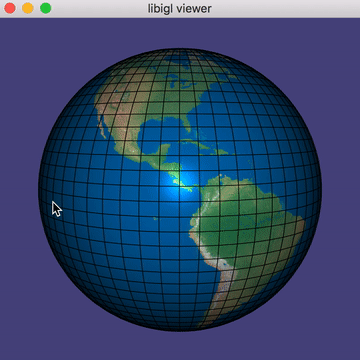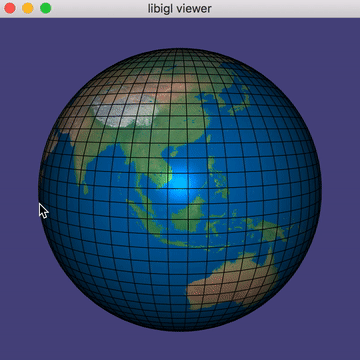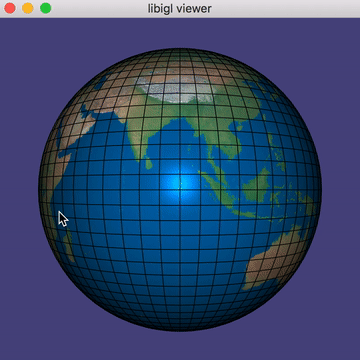
Texture mapping is a process for mapping image information (e.g., colors) onto a surface (e.g., triangle mesh). The standard way to define a texture mapping is to augment the 3D geometric information of a mesh with additional 2D parametrization information: where do we find each point on the texture image plane? Typically, parameterization coordinates are bound to the unit square.
Mapping a 3D flat polygon to 2D is rather straightforward. The problem of finding a good mapping from a 3D surface to 2D becomes much harder if our surface is not flat (e.g., like a hemisphere), if the surface does not have exact one boundary (e.g., like a sphere) or if the surface has "holes" (e.g., like a torus/doughnut).
Curved surfaces must get distorted when flattened onto the plane. This is why Greenland looks bigger than Africa on a common map of the Earth.
The lack or presence of too many boundaries or the presence of "doughnut holes" in surfaces implies that we need to "cut" the surface to lay out it on the plane so all parts of the surface are "face up". Think about trying to flatten a deflated basketball on the ground.
For a smooth surface, knowing the surface geometry (i.e., position in space) near a point fully determines the normal vector at that point.
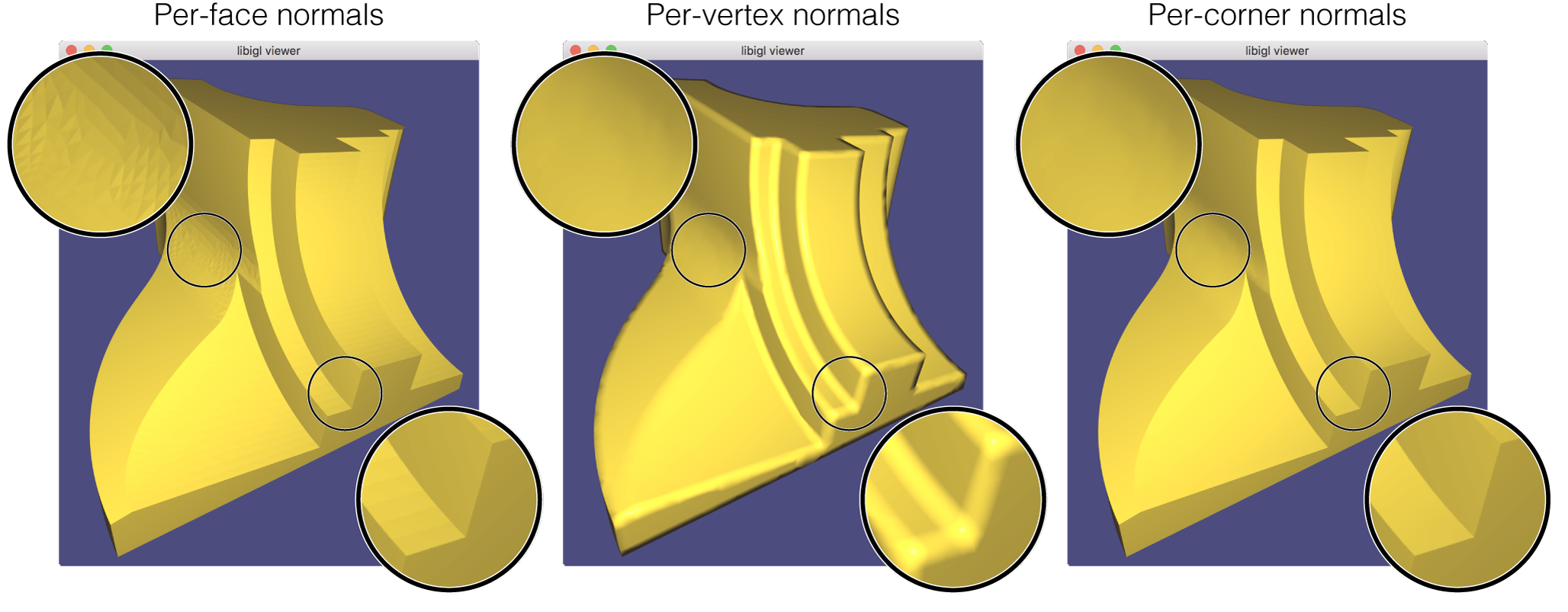
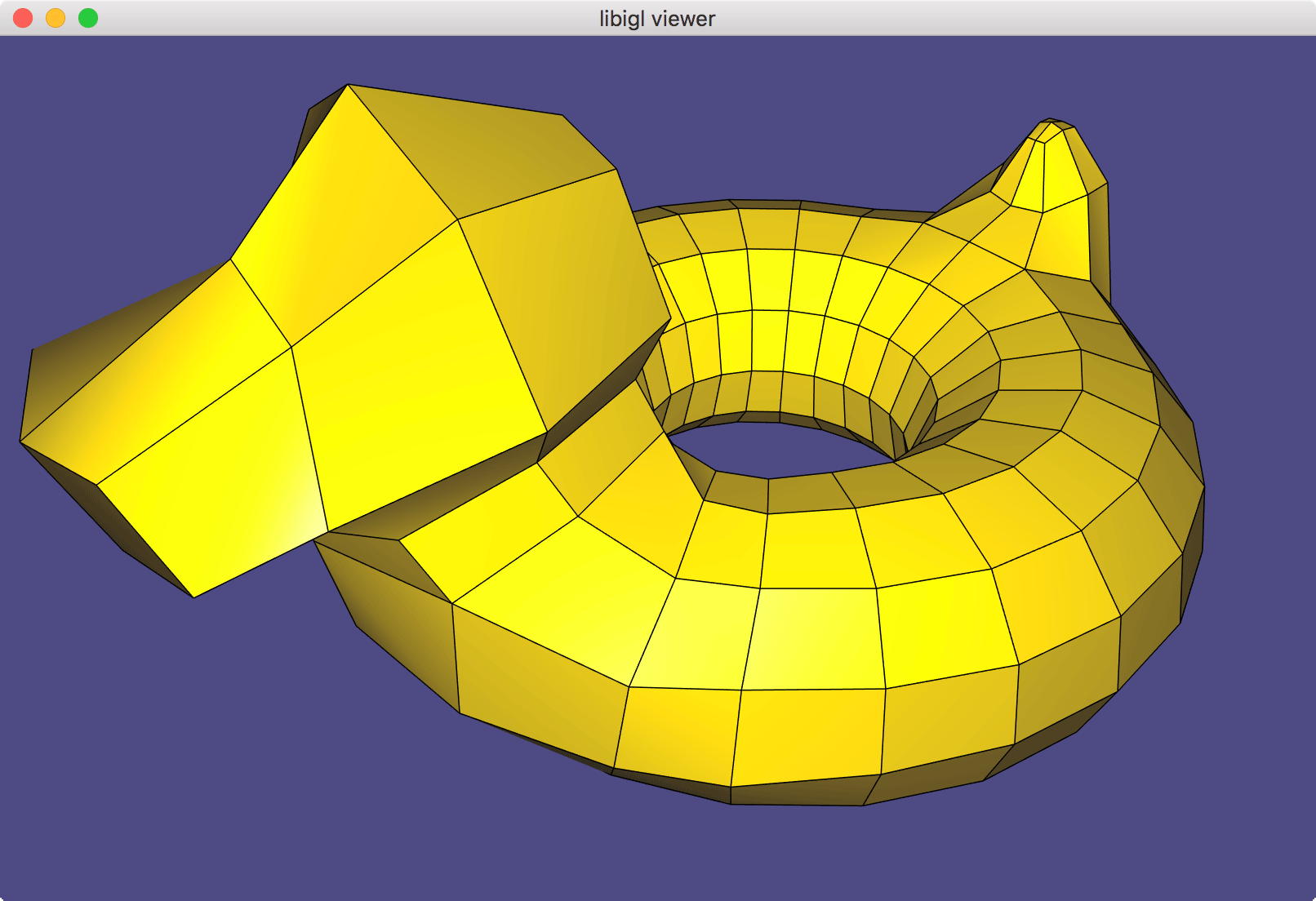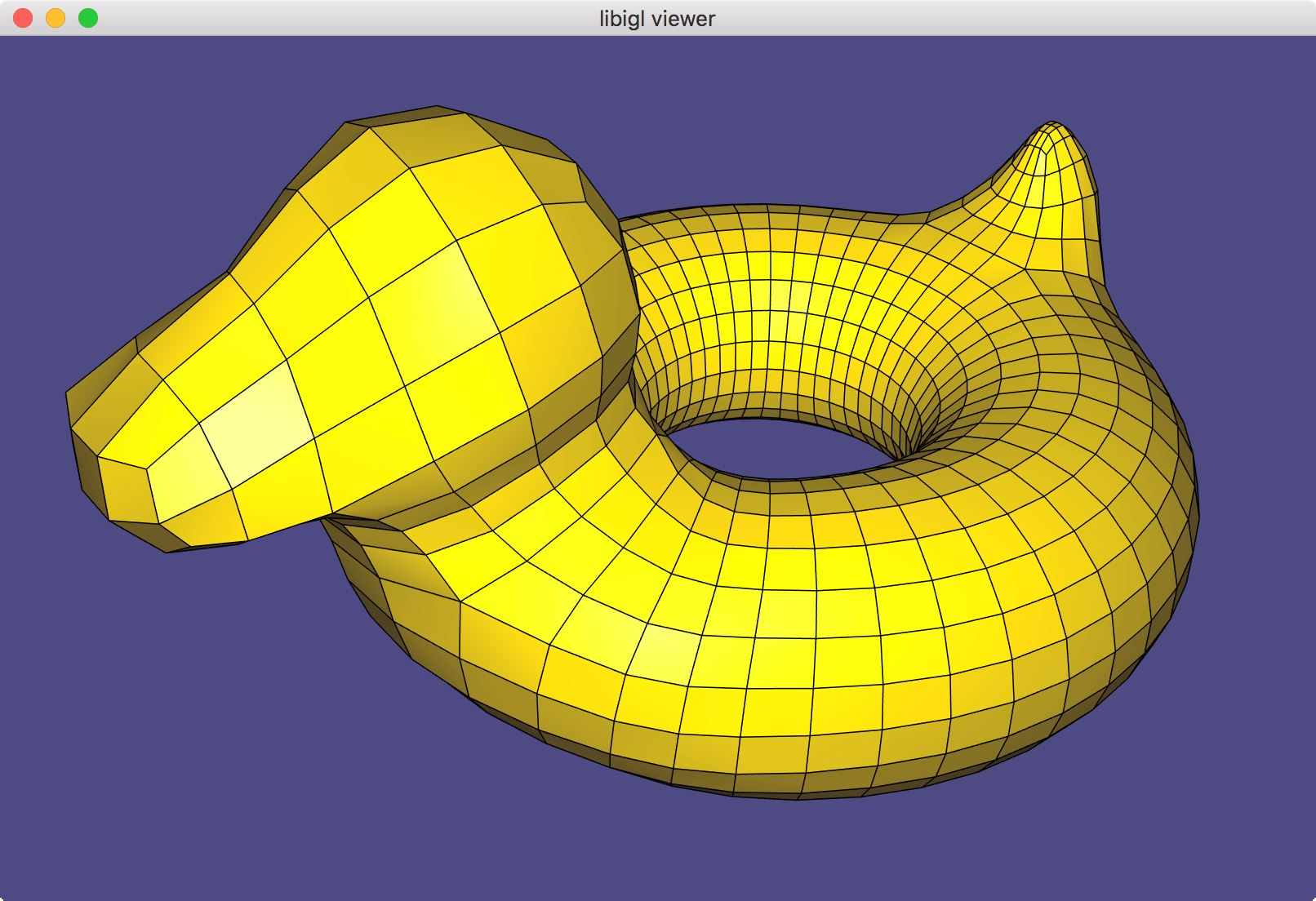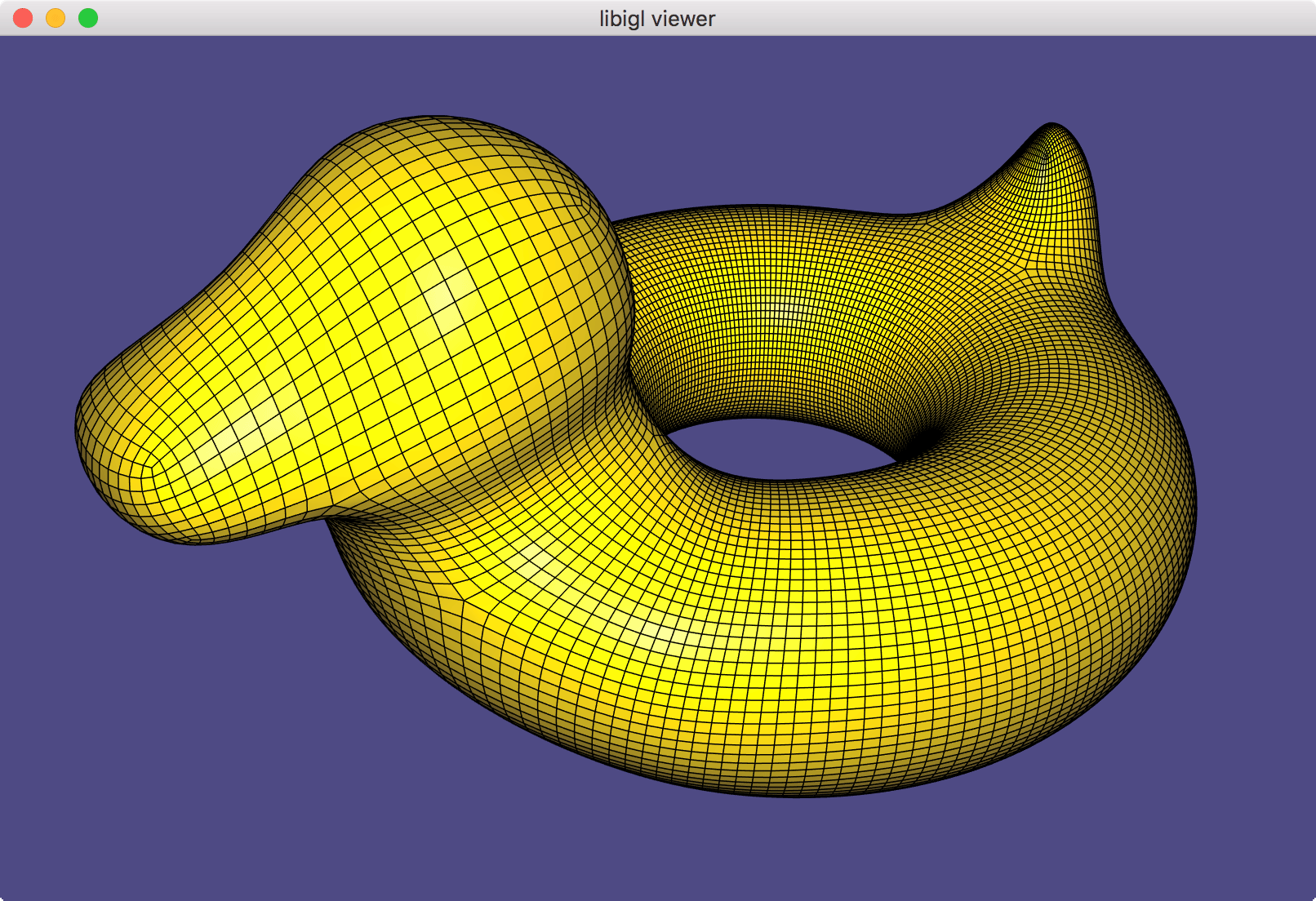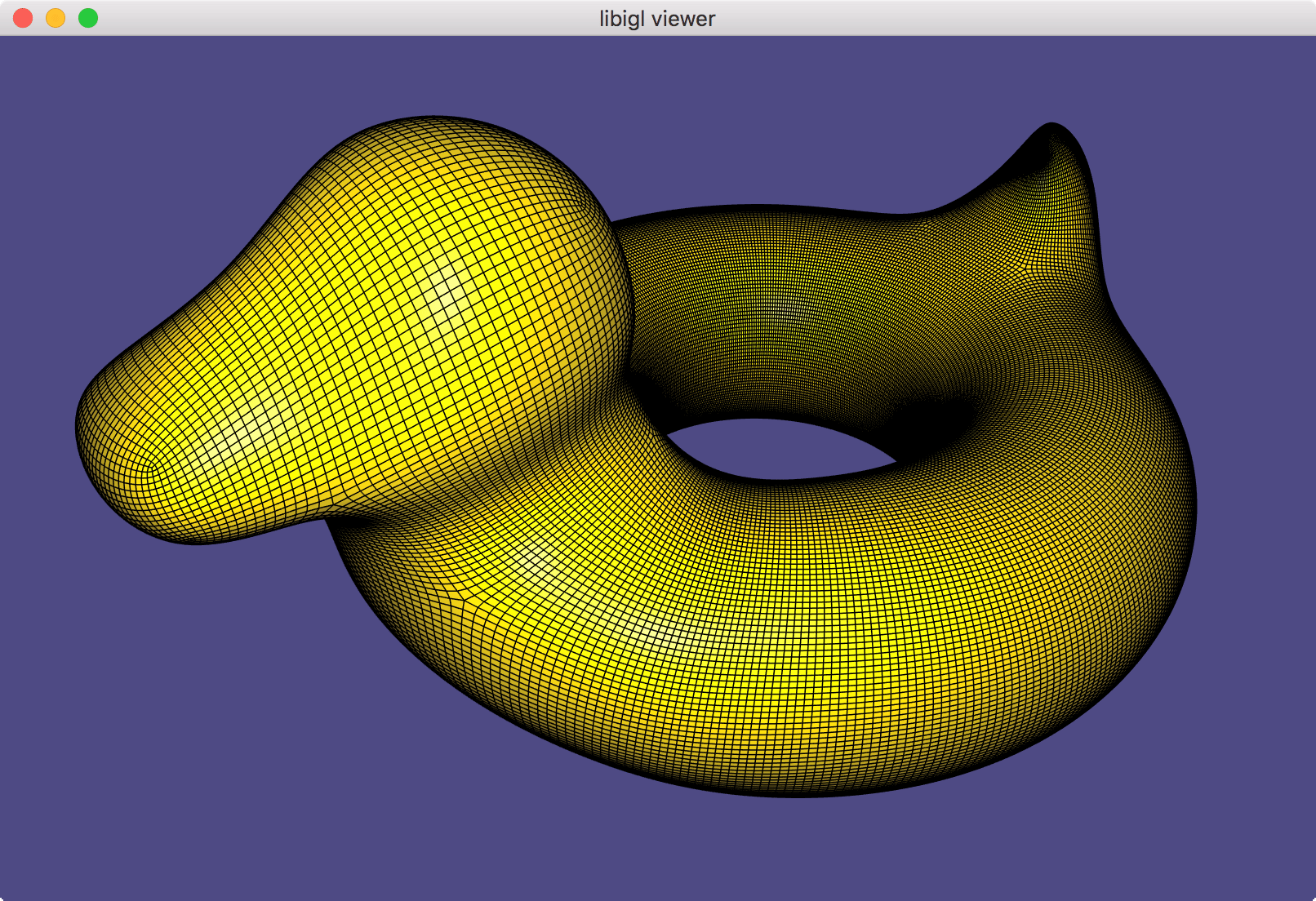
For a discrete mesh, the normal is only well-defined in the middle of planar faces (e.g., inside the triangles of a triangle mesh, but not along the edges or at vertices). Furthermore, if we use these normals for rendering, the surface will have a faceted appearance. This appearance is mathematically correct, but not necessarily desired if we wish to display a smooth looking surface.
Phong realized that linearly interpolating normals stored at the corners of each triangle leads to a smooth appearance.
This raises the question: what normals should we put at vertices or corners of our mesh?
For a faceted surface (e.g., a cube), all corners of a planar face should
share the face's normal
.
For a smooth surface (e.g., a sphere), corners of triangles located at the same vertex should share the same normal vector. This way the rendering is continuous across the vertex. A common way to define per-vertex normals is to take a weighted average of normals from incident faces. Different weighting schemes are possible: uniform average (easy, but sensitive to irregular triangulations), angle-weighted (geometrically well motivated, but not robust near zero-area triangles), area-weighted (geometrically reasonable, well behaved). In this assignment, we'll compute area-weighted per-vertex normals:
where is the set of faces neighboring the
-th vertex.
[per-vertex-normal]: images/per-vertex-normal.png height=300px ![Unique triangle normals (orange) are well-defined. We can define a notion of a normal for each vertex (purple) by taking a (weighted) average of normals from incident triangles.][per-vertex-normal]
For surfaces with a mixture of smooth-looking parts and creases, it is useful to define normals independently for each triangle corner (as opposed to each mesh vertex). For each corner, we'll again compute an area-weighted average of normals triangles incident on the shared vertex at this corner, but we'll ignore triangle's whose normal is too different from the corner's face's normal:
where is the minimum dot product between two face normals before we declare
there is a crease between them.
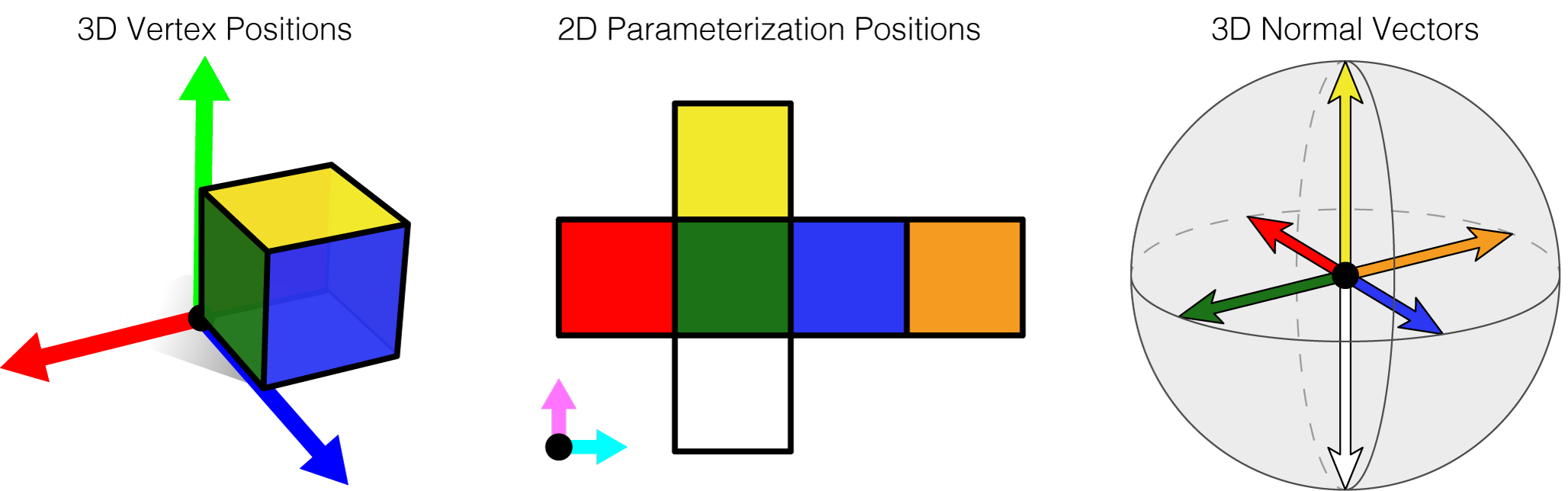
The .obj file format is a face-based representation of a mesh. The connectivity/topological data is stored implicitly by a list of a faces whose corners can share geometric information.
There are three main types of geometric information stored at vertices:
- 3D position information (let's call it
V), - 3D normal vector information (let's call it
NV), and - 2D parameterization information (let's call it
UV).
Faces know where to find the position, normal and parameterization information for each corner by following a pointer/index. For a given corner of a given face, the index for position, normal or parameterization information may be different.
Warning: In C++ indices "start" at
0, but in a .obj file the first element in a list has index1.
In this way, the quadrilateral faces of a cube mesh may use 8 unique 3D vertex positions, giving the appearance of a connected surface when visualized in 3D. The same set of faces may use 14 unique 2D parameterization positions, giving the appearance of a cross with a boundary when visualized in 2D. Finally, that same set of faces may use only 6 unique 3D normal vectors.
Every row of Eigen::MatrixXd can store a mesh vertex position using _doubles.
Every row of Eigen::MatrixXi can store a list of indices into rows of position
matrix using integers as indices.
Use .resize(num_rows,num_cols) to resize a matrix to be num_rows by
num_cols. Use X = Eigen::MatrixXd::Zero(num_rows,num_cols) to resize and initialize a
matrix with zeros.
A subdivision surface is a natural generalization of a spline curve. A smooth spline can be defined as the limit of a recursive process applied to a polygon: each edge of the polygon is split with a new vertex and the vertices are smoothed toward eachother. If you've drawn smooth curves using Adobe Illustrator, PowerPoint or Inkscape, then you've used splines.
At a high-level, subdivision surfaces work the same way. We start with a polyhedral mesh and subdivide each face. This adds new vertices on the faces and/or edges of the mesh. Then we smooth vertices toward each other.
The first and still (most) popular subdivision scheme was invented by Catmull (who went on to co-found Pixar) and Clark (founder of Silicon Graphics and Netscape). Catmull-Clark subdivision is defined for inputs meshes with arbitrary polygonal faces (triangles, quads, pentagons, etc.) but always produces a pure-quad mesh as output (i.e., all faces have 4 sides).
To keep things simple, in this assignment we'll assume the input is also a pure-quad mesh.
Mesh Lab is a free mesh-viewer used widely in computer graphics and computer vision research. Warning: Mesh Lab does not appear to respect user-provided normals in .obj files.
Autodesk Maya is a commericial 3D modeling and animation software. They often have free student versions.
You're encouraged to use #include <Eigen/Geometry> to compute the cross
product of two 3D vectors
.cross.
This assignment uses libigl for mesh viewing. libigl has many mesh processing functions implemented in C++, including some of the functions assigned here. Do not copy or look at the following implementations:
igl::per_vertex_normals
igl::per_face_normals
igl::per_corner_normals
igl::double_area
igl::vertex_triangle_adjacency
igl::writeOBJ
Write a pure-triangle or pure-quad mesh with 3D vertex positions V and faces
F, 2D parametrization positions UV and faces UF, 3D normal vectors NV
and faces NF to a .obj file.
Note: These two function overloads represent only a small subset of meshes and mesh-data that can be written to a
.objfile.
Construct the quad mesh of a cube including parameterization and per-face normals.
Hint: Draw out on paper and label with indices the 3D cube, the 2D parameterized cube, and the normals.
Construct a quad mesh of a sphere with num_faces_u × num_faces_v faces.
Compute the normal vector of a 3D triangle given its corner locations. The output vector should have length equal to the area of the triangle.
Compute per-face normals for a triangle mesh.
Compute per-vertex normals for a triangle mesh.
Compute a vertex-triangle adjacency list. For each vertex store a list of all incident faces.
Compute per corner normals for a triangle mesh by computing the area-weighted average of normals at incident faces whose normals deviate less than the provided threshold.
Conduct num_iters iterations of Catmull-Clark
subdivision on
a pure quad mesh (V,F).