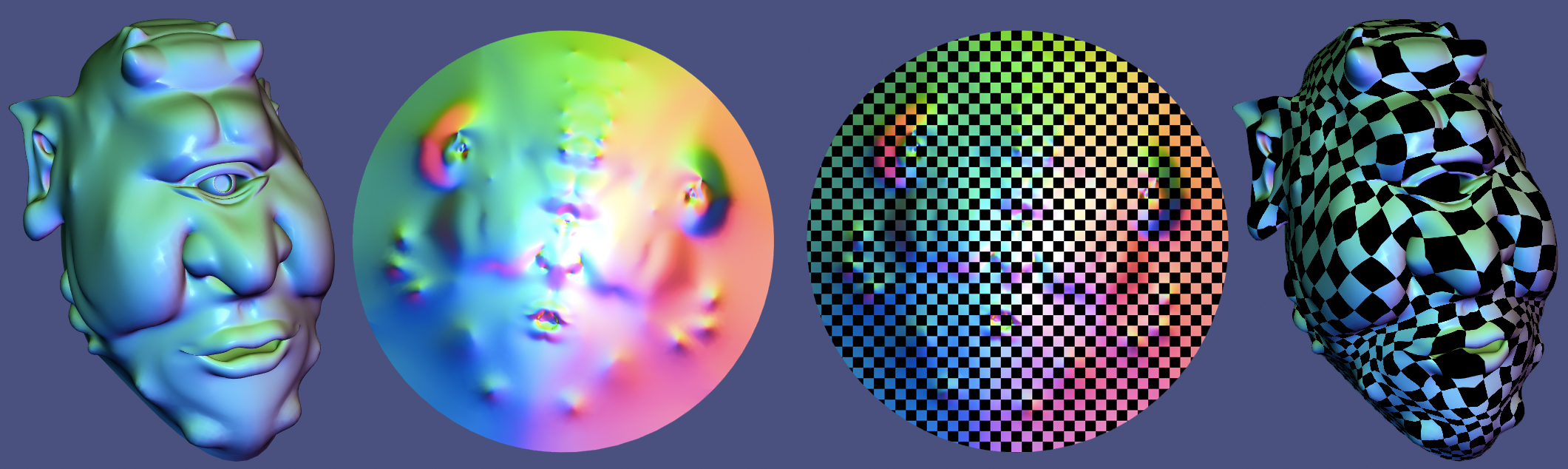To get started: Clone this repository with
git clone --recursive http://github.com/alecjacobson/geometry-processing-parameterization.git
See introduction.
Once built, you can execute the assignment from inside the build/ by running
on a given mesh:
./parameterization [path to mesh with boundary.obj]
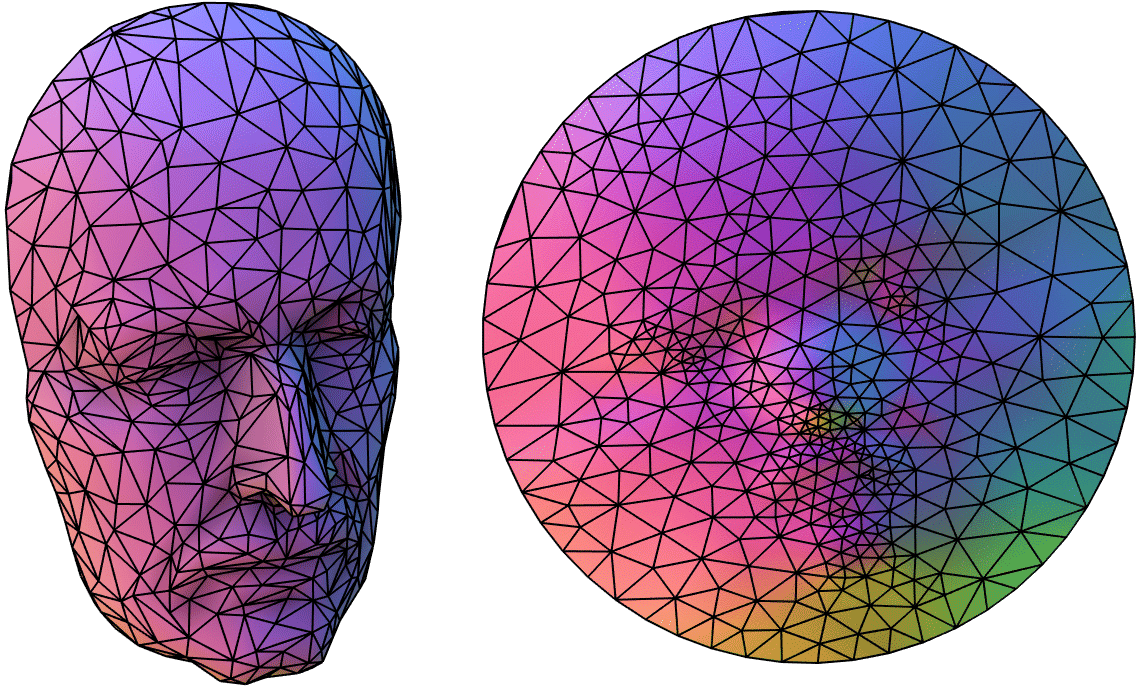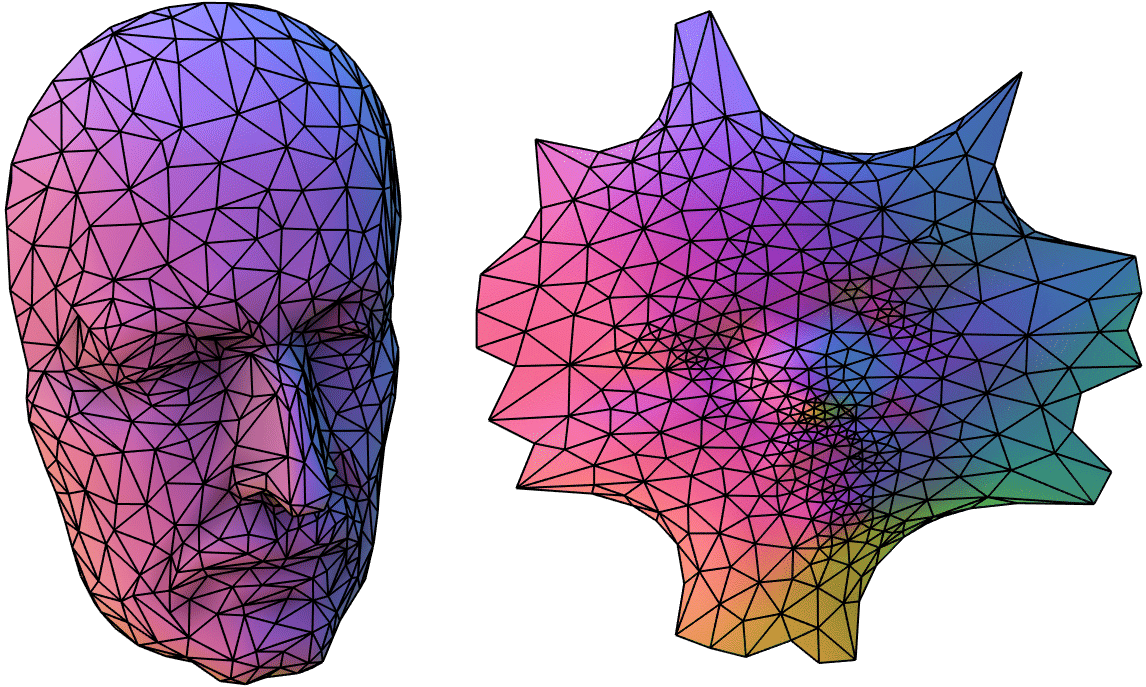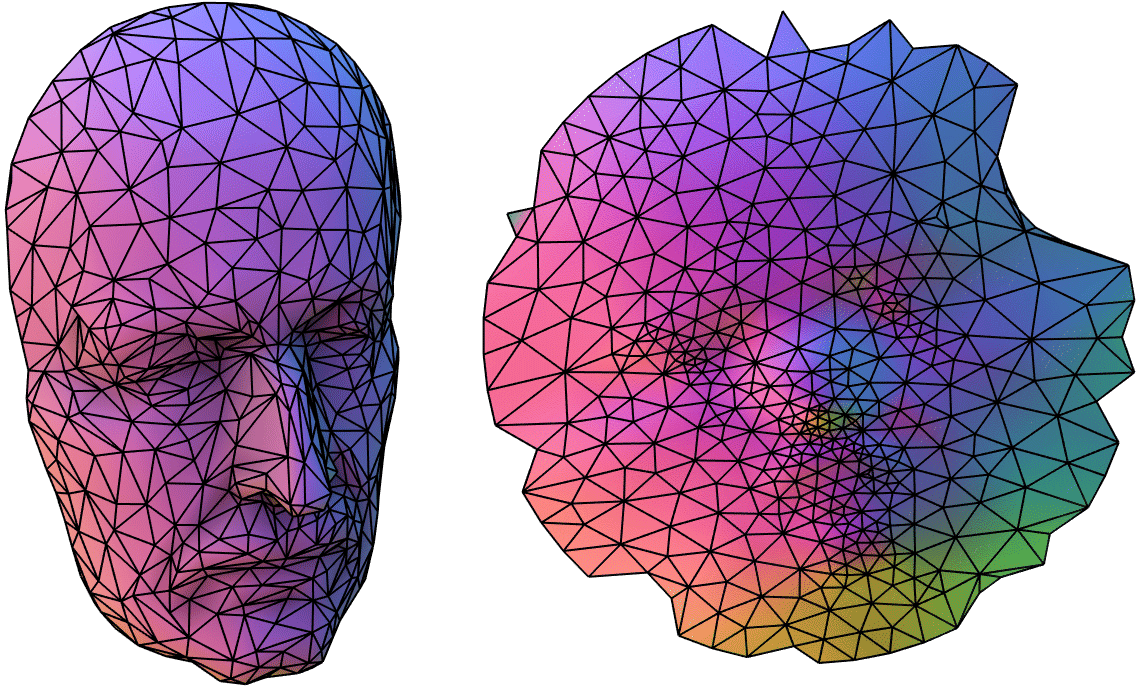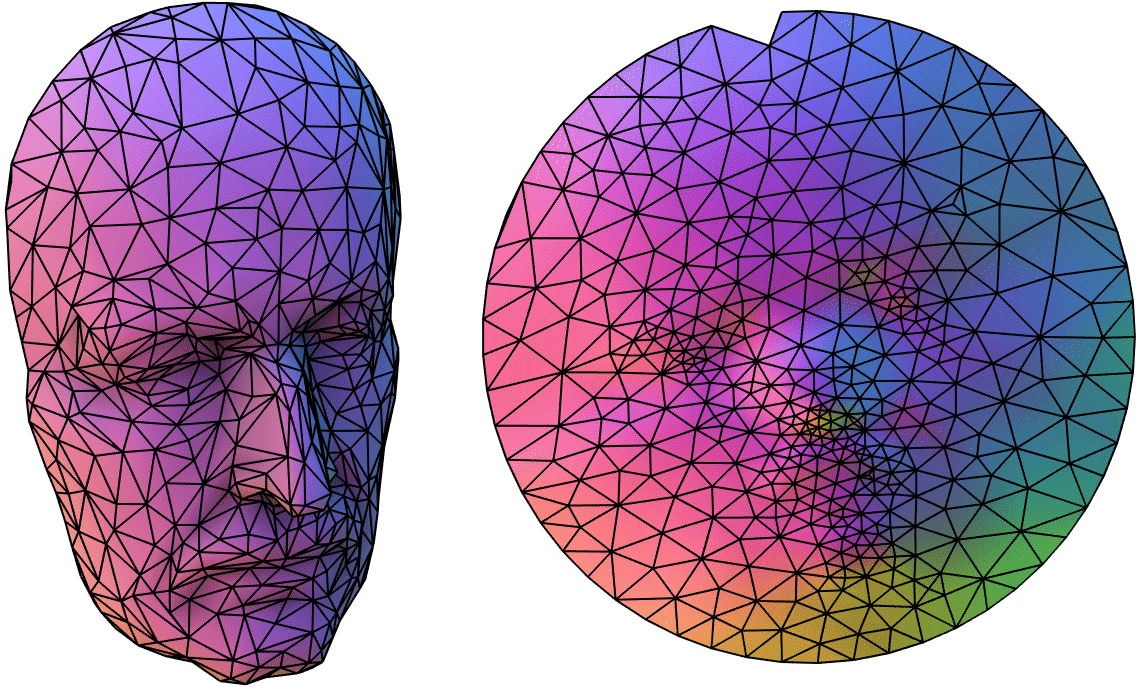
In this assignment we will explore how to flatten a surface
embedded (or even just
immersed) in
This process is often referred to as parameterization because the two-dimensional coordinate system of the flattened mesh can now be interpreted as a parameterization of the 3D surface.
A triangle mesh of a VW
Beetle is parameterized by
flattening the mesh to the
In this assignment, we are given a representation of the surface in 3D as a
triangle mesh with a list of
In general, a 3D surface cannot be flattened onto the plane without distortion. Some parts of the surface will have to be stretched and other squished. Surfaces with topological handles or without a boundary must be cut.
If we view our triangle mesh surface as a simple graph then the surface flattening problem reduces to graph drawing. Distortion can be measured in terms of the relative change in lengths between neighboring vertices.
We can pose the graph drawing problem as an optimization over node locations so that the lengths between neighboring vertices are minimized:
where
Without additional constraints, this minimization has a trivial solution: map
all vertices to the same point, e.g.,
We can avoid this by fixing the mapping of certain vertices. If we choose these
fixed vertices arbitrarily we will in general get overlaps in the flattening.
For graph drawing this means that edges cross each other; for surface
parameterization this means that multiple triangles cover the same patch of the
In 1963, Tutte showed that if the boundary of a disk-topology mesh is fixed to a convex polygon (and all spring stiffness are positive) then minimizing the energy above will result in an injective (i.e., fold-over-free) flattening.
While avoiding fold-overs is important, Tutte-style mappings suffer from a couple problems.
If uniform spring stiffness are used, then the mapping in the
We can try to remedy this by introducing a non-uniform weight or spring
stiffness
For example, we could weigh the distortion of shorter edges (on the 3D mesh)
more than longer ones:
To do this, let's write the energy minimization problem above in matrix form:
where
The degrees of freedom in our optimization are a collected in the matrix
$\mathbf{U} \in \mathbb{R}^{n\times 2}$ with two columns. The energy is written as the trace of the quadratic form (a.k.a. matrix)$\mathbf{Q} \in \mathbb{R}^{n\times n}$ applied to$\mathbf{U}$ . In effect, this is really applying$\mathbf{Q}$ to each column of$\mathbf{U}$ independently and summing the result:
$$ \begin{align*} \mathop{\text{tr}}{\left(\mathbf{U}^{\mathsf T} \mathbf{Q} \mathbf{U}\right)} &= \\ &= \mathop{\text{tr}}{\left(\mathbf{U}^{\mathsf T} \mathbf{Q} \mathbf{U}\right)} \\ &= {\mathop{\text{tr}}\left( { \left[\begin{array}{c} \mathbf{U}_1^{\mathsf T}\\ \mathbf{U}_2^{\mathsf T} \end{array}\right] \mathbf{Q} [\mathbf{U}_1 \mathbf{U}_2] } \right)} \\ &= {\mathop{\text{tr}}\left( \begin{bmatrix} \mathbf{U}_1^{\mathsf T} \mathbf{Q} \mathbf{U}_1 & \mathbf{U}_1^{\mathsf T} \mathbf{Q} \mathbf{U}_2 \\ \mathbf{U}_2^{\mathsf T} \mathbf{Q} \mathbf{U}_1 & \mathbf{U}_2^{\mathsf T} \mathbf{Q} \mathbf{U}_2 \end{bmatrix} \right)} \\ &= \mathbf{U}_1^{\mathsf T} \mathbf{Q} \mathbf{U}_1 + \mathbf{U}_2^{\mathsf T} \mathbf{Q} \mathbf{U}_2. \end{align*} $$ The benefits of energies written as the trace of a quadratic form applied to a matrix include: 1) each column can be optimized independently (assuming constraints are also separable by column), and this is often the case when columns correspond to coordinates (u, v, etc.); and 2) the quadratic form for each columns is the same (the same
$\mathbf{Q}$ ). For quadratic energy minimization, this means that we can precompute work (e.g., Cholesky facotorization) on$\mathbf{Q}$ and take advantage of it for solving with$\mathbf{U}_1$ and$\mathbf{U}_2$ and we might even solve in parallel.
We should immediately recognize this sparsity structure from the discrete
Laplacians considered in the previous assignments. If
But we have more information than edges: we know that our graph is really a
discrete representation of a two-dimensional surface. Wobbliness distortions in
the parameterization correspond to high variation in the
We can model the problem of parametrization as an energy minimization of
the variation in the
This familiar energy is called the Dirichlet energy.
We may discretize this problem immediately using piecewise linear
functions spanned by
In the smooth setting, minimizing the variation of
$u$ and$v$ will lead to an injective mapping if the boundary is constrained to a closed convex curve. In the discrete setting, poor triangle shapes in the original 3D mesh could lead to negative cotangent weights$w_{ij}$ so the positive stiffness weight assumption of Tutte's theorem is broken and fold-overs might occur. Keep in mind that positive weights are a sufficient condition for injectivity, but this does not imply that having a few negative weights will necessarily cause a fold-over. Even so, Floater proposes an alternative discrete Laplacian in "Mean value coordinates" in 2003 that retains some nice shape-preserving properties without negative weights.
Modeling distortion as an integral of variation over the given 3D surface is
going in the right direction, but so far we are treating
We can reason about distortion in terms of differential quantities of the
mapping from
We would like that regions on
where
The determinant of the Jacobian of a mapping corresponds to the scale factor by which local area expands or shrinks. This quantity also appears during integration by substitution when multivariate functions are involved.
It is tempting to try to throw this equality into a least squares energy an
minimize it. Unfortunately the determinant is already a quadratic function of
We would also like that local regions on
where
By enlisting complex analysis, we can reinterpret the mapping to the real plane
$\mathbb{R}^{2}$ as a mapping to the complex plane$\mathbb{C}$ . The angle preservation equality above corresponds to the Cauchy-Riemann equations. Complex functions that satisfy these equations are called conformal maps.
This equality is linear in
This energy was employed for surface parameterization of triangle meshes as early as "Intrinsic parameterizations of surface meshes" [Desbrun et al. 2002] and "Least squares conformal maps for automatic texture atlas generation" [Lévy et al. 2002]. Written in this form, it's perhaps not obvious how we can discretize this over a triangle mesh. Let us massage the equations a bit, starting by expanding the squared term:
We should recognize the first two terms as the Dirichlet
energies of
where we end up with the integrated determinant of the
Jacobian of the
where
If we discretize
where finally we have a simply quadratic expression: sum over all boundary
edges the determinant of the matrix with vertex positions as columns. This
quadratic form can be written as
Achtung! A naive implementation of
These are also equal to their average:
Putting this together with the Dirichlet energy terms, we can write the discrete least squares conformal mappings minimization problem as:
where
Similar to the mass-spring methods above, without constraints the least squares
conformal mapping energy will also have a trivial solution: set
To avoid this solution, we could "fix two vertices" (as originally suggested by both [Desbrun et al. 2002] and [Lévy et al. 2002]). However, this will introduce bias. Depending on the two vertices we choose we will get a different solution. If we're really unlucky, then we might choose two vertices that the energy would rather like to place near each other and so placing them at arbitrary positions will introduce unnecessary distortion (i.e., high energy).
Instead we would like natural boundary conditions (not to be confused with Neumann boundary conditions). Natural boundary conditions minimize the given energy in the absence of explicit (or essential) boundary conditions. Natural boundary conditions are convenient if we discretize the energy before differentiating to find the minimum. If our discretization is "good", then natural boundary conditions will fall out for free (natural indeed!).
To obtain natural boundary conditions without bias and avoid the trivial solution, we can require that the solution:
- minimizes the given energy,
- has non-zero norm, and
- is orthogonal to trivial solutions.
Let's break these down. The first requirement simply ensures that we're still minimizing the given energy without monkeying around with it in any way.
The second requirement adds the constraint that the solution
In our discrete case this corresponds to:
where
This is a quadratic constraint. Normally that would be bad news, but this type of constraint results in a well-studied generalized Eigen value problem.
Consider a discrete quadratic minimization problem in
$\mathbf{v} \in \mathbb{R}^n$ :
$$ \mathop{\text{min}}_{\mathbf{v}} \frac12 \mathbf{v}^{\mathsf T} \mathbf{A} \mathbf{v} \text{ subject to } \mathbf{v}^{\mathsf T} \mathbf{B} \mathbf{v} = 1, $$ where
$\mathbf{A},\mathbf{B} \in \mathbb{R}^{n \times n}$ are positive semi-definite matrices.We can enforce this constraint via the Lagrange multiplier method by introducing the scalar Lagrange multiplier
${\lambda}$ and looking for the saddle-point of the Lagrangian:
$$ \mathcal{L}(\mathbf{v},{\lambda}) = \frac12 \mathbf{v}^{\mathsf T} \mathbf{A} \mathbf{v} + {\lambda} (1 - \mathbf{v}^{\mathsf T} \mathbf{B} \mathbf{v} ). $$ This occurs when
$\partial \mathcal{L}/\partial \mathbf{v} = 0$ and$\partial \mathcal{L}/\partial {\lambda} = 0$ :
$$ \mathbf{A} \mathbf{v} - {\lambda} \mathbf{B} \mathbf{v} = 0 \Rightarrow \mathbf{A} \mathbf{v} = {\lambda} \mathbf{B} \mathbf{v} $$
$$ 1 - \mathbf{v}^{\mathsf T} \mathbf{B} \mathbf{v} = 0 \Rightarrow \mathbf{v}^{\mathsf T} \mathbf{B} \mathbf{v} = 1. \\ $$ This is the canonical form of the generalized Eigen value problem for which there are available numerical algorithms.
Finally, our third constraint is that the solution is orthogonal to the trivial
solutions. There are two trivial solutions. They correspond to mapping all
This eigenvector is sometimes called the Fiedler vector.
The least squares conformal mapping energy is invariant to translation and
rotation. The eigen decomposition process described above will naturally take
care of "picking" a canonical translation by pulling the solution
We can try to find a canonical rotation by using principle component
analysis on the
returned
For mappings with strong reflectional symmetry then singular value
decomposition on the covariance
matrix
If the surface has only a small boundary then all of the surface will have to be packed inside the interior. We're not directly punishing area distortion so in order to satisfy the angle distortion. Freeing the boundary helps a little, but ultimately the only way to mitigate this is to: 1) trade area distortion for angle distortion or 2) cut (a.k.a. "interrupt") the mapping with discontinuities (see, e.g., Goode homolosine projection used for maps of Earth).
Cutting new boundaries is always necessary for parameterizing closed surfaces. There has been much work in the last few years on choosing cuts automatically, many of which are good candidates for a final implementation project.
igl::harmonicigl::lscmigl::vector_area_matrix
igl::boundary_loopigl::cotmatrix(or your previous implementation)igl::eigs(Use theigl::EIGS_TYPE_SMtype)igl::map_vertices_to_circleigl::massmatrix(or your previous implementation)igl::min_quad_with_fixed(for minimizing a quadratic energy subject to fixed value constraints)igl::repdiag
Given a 3D mesh (V,F) with a disk topology (i.e., a manifold with single
boundary), compute a 2D parameterization according to Tutte's mapping inside
the unit disk. All boundary vertices should be mapped to the unit circle and
interior vertices mapped inside the disk without flips.
Constructs the symmetric area matrix A, s.t. [V.col(0)' V.col(1)'] * A * [V.col(0); V.col(1)] is the vector area of the mesh (V,F).
Given a 3D mesh (V,F) with boundary compute a 2D parameterization that
minimizes the "least squares conformal" energy:
where U.
Use eigen-decomposition to find an un-biased, non-trivial minimizer. Then use
singular value decomposition to find a canonical rotation to line the principle
axis of