pomegranate is a package for graphical models and Bayesian statistics for Python, implemented in cython. It grew out of the YAHMM package, where many of the components used could be rearranged to do other cool things. It currently supports:
- Probability Distributions
- Finite State Machines
- Hidden Markov Models
- Discrete Bayesian Networks
- General Mixture Models
See the tutorial below, or the more in depth tutorials in the tutorials folder with examples in IPython notebooks.
No good project is done alone, and so I'd like to thank all the previous contributors to YAHMM, and all the current contributors to pomegranate, including the graduate students who share my office I annoy on a regular basis by bouncing ideas off of.
pomegranate is now pip installable! Install using pip install pomegranate. You can get the bleeding edge using the following:
git clone https://github.com/jmschrei/pomegranate.git
cd pomegranate
python setup.py install
Lastly, you can also download the zip and manually move the files into your site-packages folder (or your PYTHON_PATH, if you've changed it).
If you would like to contribute a feature then fork the master branch (fork the release if you are fixing a bug). Be sure to run the tests before changing any code. You'll need to have nosetests installed. The following command will run all the tests:
nosetests -s -v tests/
Let us know what you want to do just in case we're already working on an implementation of something similar. This way we can avoid any needless duplication of effort. Also, please don't forget to add tests for any new functions.
The emission distributions used later on for the other models can be used independently. This is useful if you want to calculate the probability of some data given a distribution, or had to fit a distribution to some given data. pomegranate offers a simple solution, which is an extensible library of distributions and kernel densities natively built in.
from pomegranate import *
a = NormalDistribution( 5, 2 )
b = TriangleKernelDensity( [1,5,2,3,4], weights=[4,2,6,3,1] )
c = MixtureDistribution( [ NormalDistribution( 2, 4 ), ExponentialDistribution( 8 ) ], weights=[1, 0.01] )
print a.log_probability( 8 )
print b.log_probability( 8 )
print c.log_probability( 8 )This should return -2.737, -inf, and -3.44 respectively.
We can also update these distributions using Maximum Likelihood Estimates for the new values. Kernel densities will discard previous points and add in the new points, while MixtureDistributions will perform expectation-maximization to update the mixture of distributions.
c.from_sample([1, 5, 7, 3, 2, 4, 3, 5, 7, 8, 2, 4, 6, 7, 2, 4, 5, 1, 3, 2, 1])
print cThis should result in MixtureDistribution( [NormalDistribution(3.916, 2.132), ExponentialDistribution(0.99955)], [0.9961, 0.00386] ). All distributions can be trained either as a batch using from_sample, or using summary statistics using summarize on lists of numbers until all numbers have been fed in, and then from_summaries like in the following example which produces the same result:
c = MixtureDistribution( [ NormalDistribution( 2, 4 ), ExponentialDistribution( 8 ) ], weights=[1, 0.01] )
c.summarize([1, 5, 7, 3, 2, 4, 3])
c.summarize([5, 7, 8])
c.summarize([2, 4, 6, 7, 2, 4, 5, 1, 3, 2, 1])
c.from_summaries()Splitting up the data into batches will still give an exact answer, but allows for out of core training of distributions on massive amounts of data.
In addition, training can be done on weighted samples by passing an array of weights in along with the data for any of the training functions, such as c.summarize([5,7,8], weights=[1,2,3]). Training can also be done with inertia, where the new value will be some percentage the old value and some percentage the new value, used like c.from_sample([5,7,8], inertia=0.5) to indicate a 50-50 split between old and new values.
Finite state machines are computational machines which can be in one of many states. The machine can be defined as a graphical model where the states are the states of the machine, and the edges define the transitions from each state to the other states in the machine. As the machine receives data, the state which it is in changes in a greedy fashion. Since the machine can be in only one state at a time and is memoryless, it is extremely useful. A classic example is a turnstile, which can take in nickels, dimes, and quarters, but only needs 25 cents to pass.
from pomegranate import *
# Create the states in the same way as you would an HMM
a = State( None, "5" )
b = State( None, "10" )
c = State( None, "15" )
d = State( None, "20" )
e = State( None, "25" )
# Create a FiniteStateMachine object
model = FiniteStateMachine( "Turnstile" )
# Add the states in the same way
model.add_states( [a, b, c, d, e] )
# Add in transitions by using nickels
model.add_transition( model.start, a, 5 )
model.add_transition( a, b, 5 )
model.add_transition( b, c, 5 )
model.add_transition( c, d, 5 )
model.add_transition( d, e, 5 )
# Add in transitions using dimes
model.add_transition( model.start, b, 10 )
model.add_transition( a, c, 10 )
model.add_transition( b, d, 10 )
model.add_transition( c, e, 10 )
# Add in transitions using quarters
model.add_transition( model.start, e, 25 )
# Bake the model in the same way
model.bake()In the above example, the name of the states encodes information about the state, and the edges each hold keys as to what cas pass along them. There are no distributions on these states, as this is not a probabilistic model, but distributions can be added without breaking the code if they are useful information to have on each state.
# Take a sequence of observations
seq = [ 5, 25, 10 ]
# Print out where you start in the model
print model.current_state.name
# Print out where the model is for each step
for symbol in seq:
i = model.current_state.name
model.step( symbol )
print "Inserted {}: Moving from {} to {}.".format( symbol, i, model.current_state.name )yields
Turnstile-start
Inserted 5: Moving from Turnstile-start to 5.
Inserted 5: Moving from 5 to 10.
Inserted 5: Moving from 10 to 15.
Inserted 5: Moving from 15 to 20.
Inserted 5: Moving from 20 to 25.
As we add nickles, we progress through the machine. But if we restarted and tried to do something invalid, we get the following, without progressing in the state machine:
# Take a sequence of coins to add to the model
seq = [ 5, 25, 10 ]
# Print out where you start in the model
print model.current_state.name
# Print out where the model is for each step
for symbol in seq:
i = model.current_state.name
model.step( symbol )
print "Inserted {}: Moving from {} to {}.".format( symbol, i, model.current_state.name )yields
Turnstile-start
Inserted 5: Moving from Turnstile-start to 5.
Exception SyntaxError('No edges leaving state 5 with key 25') in 'pomegranate.fsm.FiniteStateMachine._step' ignored
Inserted 10: Moving from 5 to 15.
Presumably there would be client code surrounding the state machine to see where it is at each position, and do something based on which state it is currently in.
Hidden Markov Models
Hidden Markov models are a form of structured learning, in which a sequence of observations are labelled according to the hidden state they belong. HMMs can be thought of as non-greedy FSMs, in that the assignment of tags is done in a globally optimal way as opposed to being simply the best at the next step. HMMs have been used extensively in speech recognition and bioinformatics, where speech is a sequence of phonemes and DNA is a sequence of nucleotides.
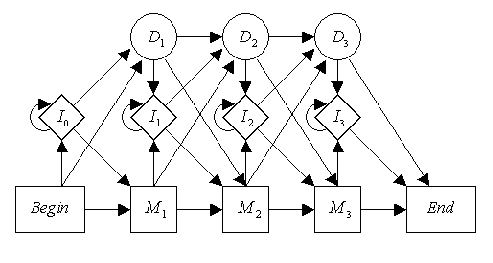
A full tutorial on sequence alignment in bioinformatics can be found here The gist is that you have a graphical structure as follows:
This defines a 'profile HMM' of length 3, in which you model the a profile and align new sequences to it. A perfectly matching sequence will align its three characters to the three match states. However, there can be mismatches where the observed sequence does not match the profile perfectly, which is why each emission is a distribution over all four nucleotides with small probabilities of seeing other nucleotides. There can also be insertions into the sequence, modelled by the middle track, and deleted in comparison to the profile modelled by the top track of silent states. This type of model can solve an interesting question in sequence analysis of when is it more likely that a nucleotide mutated over time (simply a mismatch in the model), versus was explicitly removed and had a new nucleotide added in (delete + insertion). We can see which is more likely using the Viterbi algorithm.
Lets make our profile we model 'ACT'.
from pomegranate import *
model = HiddenMarkovModel( "Global Sequence Aligner" )
# Define the distribution for insertions
i_d = DiscreteDistribution( { 'A': 0.25, 'C': 0.25, 'G': 0.25, 'T': 0.25 } )
# Create the insert states, each with a uniform insertion distribution
i0 = State( i_d, name="I0" )
i1 = State( i_d, name="I1" )
i2 = State( i_d, name="I2" )
i3 = State( i_d, name="I3" )
# Create the match states with small chances of mismatches
m1 = State( DiscreteDistribution({ "A": 0.95, 'C': 0.01, 'G': 0.01, 'T': 0.02 }) , name="M1" )
m2 = State( DiscreteDistribution({ "A": 0.003, 'C': 0.99, 'G': 0.003, 'T': 0.004 }) , name="M2" )
m3 = State( DiscreteDistribution({ "A": 0.01, 'C': 0.01, 'G': 0.01, 'T': 0.97 }) , name="M3" )
# Create the silent delete states
d1 = State( None, name="D1" )
d2 = State( None, name="D2" )
d3 = State( None, name="D3" )
# Add all the states to the model
model.add_states( [i0, i1, i2, i3, m1, m2, m3, d1, d2, d3 ] )
# Create transitions from match states
model.add_transition( model.start, m1, 0.9 )
model.add_transition( model.start, i0, 0.1 )
model.add_transition( m1, m2, 0.9 )
model.add_transition( m1, i1, 0.05 )
model.add_transition( m1, d2, 0.05 )
model.add_transition( m2, m3, 0.9 )
model.add_transition( m2, i2, 0.05 )
model.add_transition( m2, d3, 0.05 )
model.add_transition( m3, model.end, 0.9 )
model.add_transition( m3, i3, 0.1 )
# Create transitions from insert states
model.add_transition( i0, i0, 0.70 )
model.add_transition( i0, d1, 0.15 )
model.add_transition( i0, m1, 0.15 )
model.add_transition( i1, i1, 0.70 )
model.add_transition( i1, d2, 0.15 )
model.add_transition( i1, m2, 0.15 )
model.add_transition( i2, i2, 0.70 )
model.add_transition( i2, d3, 0.15 )
model.add_transition( i2, m3, 0.15 )
model.add_transition( i3, i3, 0.85 )
model.add_transition( i3, model.end, 0.15 )
# Create transitions from delete states
model.add_transition( d1, d2, 0.15 )
model.add_transition( d1, i1, 0.15 )
model.add_transition( d1, m2, 0.70 )
model.add_transition( d2, d3, 0.15 )
model.add_transition( d2, i2, 0.15 )
model.add_transition( d2, m3, 0.70 )
model.add_transition( d3, i3, 0.30 )
model.add_transition( d3, model.end, 0.70 )
# Call bake to finalize the structure of the model.
model.bake()
for sequence in map( list, ('ACT', 'GGC', 'GAT', 'ACC') ):
logp, path = model.viterbi( sequence )
print "Sequence: '{}' -- Log Probability: {} -- Path: {}".format(
''.join( sequence ), logp, " ".join( state.name for idx, state in path[1:-1] ) )This should produce the following:
Sequence: 'ACT' -- Log Probability: -0.513244900357 -- Path: M1 M2 M3
Sequence: 'GGC' -- Log Probability: -11.0481012413 -- Path: I0 I0 D1 M2 D3
Sequence: 'GAT' -- Log Probability: -9.12551967402 -- Path: I0 M1 D2 M3
Sequence: 'ACC' -- Log Probability: -5.08795587886 -- Path: M1 M2 M3
This seems to work well. A perfect match goes through the three match states, and off matches go through other sequences of hidden states. We see in the case of ACC, the model thinks it's more likely that the T at the end of the profile was mutated to a C than a deletion and an insertion, but is not so lenient in the case of 'GGC'. This is I made G's very unlikely in our prior match distributions.
The HMM can then be used as a backend to do the alignment by defining a function which takes in two sequences, and uses the HMM in the global name space to do the alignment (works for this example, but using global name spaces in general is a bad idea). Using the HMM as a backend allows us to shield users from needing to know how HMMs work at all but only that through the power of math their sequences have been aligned.
def pairwise_alignment( x, y ):
"""
This function will take in two sequences, and insert dashes appropriately to make them appear aligned. This consists only of adding a dash to the model sequence for every insert in the path appropriately, and a dash in the observed sequence for every delete in the path appropriately.
"""
logp, path = model.viterbi( sequence )
for i, (index, state) in enumerate( path[1:-1] ):
name = state.name
if name.startswith( 'D' ):
y = y[:i] + '-' + y[i:]
elif name.startswith( 'I' ):
x = x[:i] + '-' + x[i:]
return x, y
for sequence in map( list, ('A', 'GA', 'AC', 'AT', 'ATCC' ) ):
x, y = pairwise_alignment( 'ACT', ''.join(sequence) )
print "{}\n{}".format( x, y )
printyields
Sequence: A
ACT
A--
Sequence: GA
-ACT
GA--
Sequence: AC
ACT
AC-
Sequence: AT
ACT
A-T
Sequence: ATCC
ACT--
A-TCC
Everything is exactly the same as in YAHMM, except the Model class is now HiddenMarkovModel. If you have code using YAHMM you would like to port over to pomegranate, the only difference is the start of your file should have
from pomegranate import *
from pomegranate import HiddenMarkovModel as Modelinstead of
from yahmm import *Bayesian networks are a powerful inference tool, in which nodes represent some random variable we care about, edges represent dependencies and a lack of an edge between two nodes represents a conditional independence. A powerful algorithm called the sum-product or forward-backward algorithm allows for inference to be done on this network, calculating posteriors on unobserved ("hidden") variables when limited information is given. The more information is known, the better the inference will be, but there is no requirement on the number of nodes which must be observed. If no information is given, the marginal of the graph is trivially calculated. The hidden and observed variables do not need to be explicitly defined when the network is set, they simply exist based on what information is given.
Lets test out the Bayesian Network framework on the Monty Hall problem. The Monty Hall problem arose from the gameshow Let's Make a Deal, where a guest had to choose which one of three doors had a prize behind it. The twist was that after the guest chose, the host, originally Monty Hall, would then open one of the doors the guest did not pick and ask if the guest wanted to switch which door they had picked. Initial inspection may lead you to believe that if there are only two doors left, there is a 50-50 chance of you picking the right one, and so there is no advantage one way or the other. However, it has been proven both through simulations and analytically that there is in fact a 66% chance of getting the prize if the guest switches their door, regardless of the door they initially went with.
We can reproduce this result using Bayesian networks with three nodes, one for the guest, one for the prize, and one for the door Monty chooses to open. The door the guest initially chooses and the door the prize is behind are completely random processes across the three doors, but the door which Monty opens is dependent on both the door the guest chooses (it cannot be the door the guest chooses), and the door the prize is behind (it cannot be the door with the prize behind it).
import math
from pomegranate import *
# The guests initial door selection is completely random
guest = DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# The door the prize is behind is also completely random
prize = DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# Monty is dependent on both the guest and the prize.
monty = ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
# State objects hold both the distribution, and a high level name.
s1 = State( guest, name="guest" )
s2 = State( prize, name="prize" )
s3 = State( monty, name="monty" )
# Create the Bayesian network object with a useful name
network = BayesianNetwork( "Monty Hall Problem" )
# Add the three states to the network
network.add_states( [ s1, s2, s3 ] )
# Add transitions which represent conditional dependencies, where the second node is conditionally dependent on the first node (Monty is dependent on both guest and prize)
network.add_transition( s1, s3 )
network.add_transition( s2, s3 )
network.bake()Bayesian Networks introduc a new distribution, the ConditionalDiscreteDistribution. This distribution takes in (1) a dictionary where each nested layer refers to the values one of the distributions it is dependent on takes and (2) a list of the distribution objects it is dependent on in the order of the nesting in the dictionary. In the Monty Hall example, the monty distribution is dependent on both the guest and the prize distributions in that order. The first layer of nesting accounts for what happens when the guest chooses various doors, and the second layer indicates what happens when the prize is actually behind a certain door, for each of the 9 possibilities.
In order to reproduce the final result, we need to take advantage of the forward-backward/sum-product algorithm. This algorithm allows the network to calculate posterior probabilities for each distribution in the network when as distributions get clamped to certain values. This is done in pomegranate by feeding in a dictionary of state names and their associated values, and running forward_backward.
Lets say that the guest chooses door 'A'. guest becomes an observed variable, while both prize and monty are hidden variables.
observations = { 'guest' : 'A' }
# beliefs will be an array of posterior distributions or clamped values for each state, indexed corresponding to the order
# in self.states.
beliefs = network.forward_backward( observations )
# Convert the beliefs into a more readable format
beliefs = map( str, beliefs )
# Print out the state name and belief for each state on individual lines
print "\n".join( "{}\t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) )This will yield:
prize DiscreteDistribution({'A': 0.3333333333333335, 'C': 0.3333333333333333, 'B': 0.3333333333333333})
guest DiscreteDistribution({'A': 1.0, 'C': 0.0, 'B': 0.0})
monty DiscreteDistribution({'A': 0.0, 'C': 0.5, 'B': 0.5})
Since we have clamped the guest distribution to 'A', it returns just that value. The prize distribution is unaffected. Since guest is clamped to 'A', it is forced to stay that way. Note that the prize distribution is unaffected, but that the monty distribution now puts a 0 probability on him saying A, since he will not open the same door the guest chose.
In order to reproduce the final result, we need to see what happens when Monty opens a door. Lets clamp the Monty distribution to 'B' to indicate he has opened that door. Now both guest and monty are observed variables, and prize is the hidden variable.
observations = { 'guest' : 'A', 'monty' : 'B' }
beliefs = map( str, network.forward_backward( observations ) )
print "\n".join( "{}\t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) )yields
guest DiscreteDistribution({'A': 1.0, 'C': 0.0, 'B': 0.0})
monty DiscreteDistribution({'A': 0.0, 'C': 0.0, 'B': 1.0})
prize DiscreteDistribution({'A': 0.3333333333333333, 'C': 0.6666666666666666, 'B': 0.0})
Both guest and monty have been clamped to values. However, we see that probability of prize being 'C' is 66% mimicking the mystery behind the Monty hall problem!
This has predominately leveraged forward propogation of messages. If we want to see backward propogation of messages, lets see what happens if we tuned in late and only saw which door Monty opened. Monty is an observed variable, while both guest and prize are hidden variables.
observations = { 'monty' : 'B' }
beliefs = map( str, network.forward_backward( observations ) )
print "\n".join( "{}\t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) )yields
guest DiscreteDistribution({'A': 0.49999999999999994, 'C': 0.49999999999999994, 'B': 0.0})
monty DiscreteDistribution({'A': 0.0, 'C': 0.0, 'B': 1.0})
prize DiscreteDistribution({'A': 0.49999999999999994, 'C': 0.49999999999999994, 'B': 0.0})
We know that if Monty opened door 'B', that the prize cannot be behind 'B' and that the guest could not have opened 'B'. The posterior guest and prize probabilities show this.
Useful stuff.